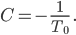Lila kann gar nicht aufhören, Max von Funktionen zu erzählen, die Schwingungen und Erdbeben modellieren. Sie hat weitere anspruchsvolle Funktionen des Geologen und Erdbeben- und Nukleartestforschers von Seggern entdeckt. Diesmal ist es schwieriger, die zu berechnen. Jetzt hat sie bei t = 0 eine Division durch Null und braucht ihre Analysis-Kenntnisse, die sie bei Kubicki erworben hat.
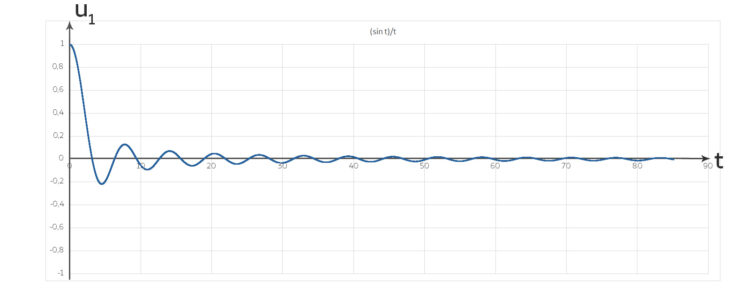
Lila Max, findest du nicht auch diese Schwingungen ganz schön? Hier, eine Schwingung mit abklingender Amplitude:
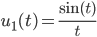
Max Lila, na, am Ende ist fast nichts mehr zu sehen von der Schwingung. Aber am Anfang, wie hast du denn
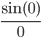
ausgerechnet?
Lila Da konnte ich gut meine Analysis-Kenntnisse benutzen, irgendwie ist es doch nützlich, was Kubicki uns erzählt hat. Wenn du nämlich mit einem Tabellenkalkulationsprogramm sin (0)/0 ausrechnest, kriegst du eine Fehlermeldung. Also habe ich diesen Punkt extra behandelt.
Max Aha!
Grenzwerte bei „0/0“
Lila Natürlich ist die Funktion u1 nur für t ≠ 0 definiert, man kann aber den Grenzwert ausrechnen:
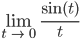
Da gibt es die hospitalsche Regel, die sagt, wenn du den Grenzwert eines Quotienten bestimmen willst, wo beide Funktionen nach Null gehen, und beide Funktionen diffbar sind, ...
Max ... Jetzt sprichst du schon wieder wie eine Mathematikerin!
Lila Sorry, ... und beide Funktionen differenzierbar sind, dann kannst du anstelle der Funktionen ihre Ableitung nehmen:
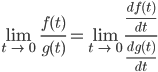
Max Hm, wenn etwas nach Null geht, dann entscheiden die Geschwindigkeiten darüber?
Lila Ja, genau! In dem Fall können wir das wunderbar ausrechnen:
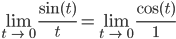
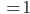
Max Krass!
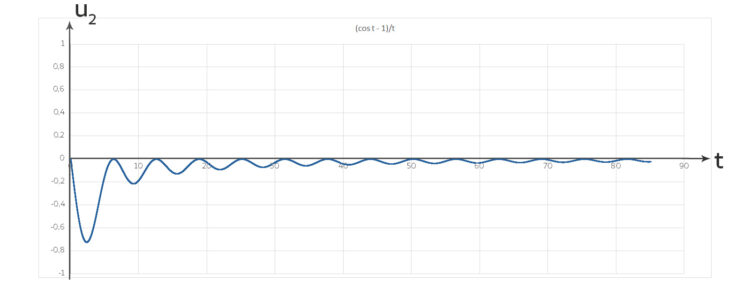
Lila Und als Analogon zu dieser 1. Funktion hat von Seggern eine ähnliche Funktion u2 mit dem Kosinus gefunden:
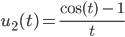
Trigonometrische Integrale
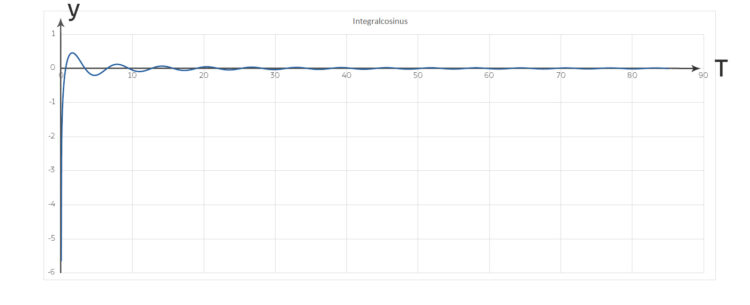
Wenn man dann noch die Funktionen u1 und u2 von 0 bis T integriert, kommt man auf die trigonometrischen Integrale, den Integralsinus
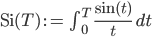
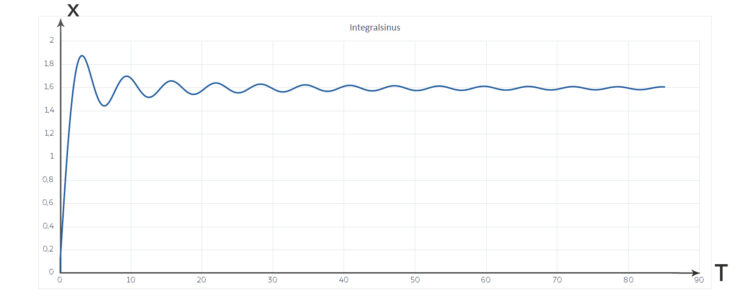
und den Integralkosinus
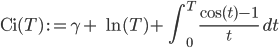
Der ist leider etwas komplizierter, da stecken noch der Logarithmus und die Euler-Mascheroni-Konstante γ
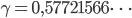
drin. Die beiden trigonometrischen Integrale habe ich wieder numerisch integriert, wie beim letzten Mal bei den Fresnel-Integralen. Nur beim Integralkosinus hatte ich Schwierigkeiten, den Punkt bei T = 0 zu zeichnen.
Max Naja,
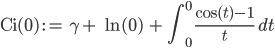
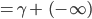

Wie hast du das deinem Tabellenkalkulationsprogramm beigebracht?
Lila Da habe ich mir was ausgedacht! Ich muss ja gar nicht den Punkt (0, - ∞) zeichnen!
Max Na, gut!
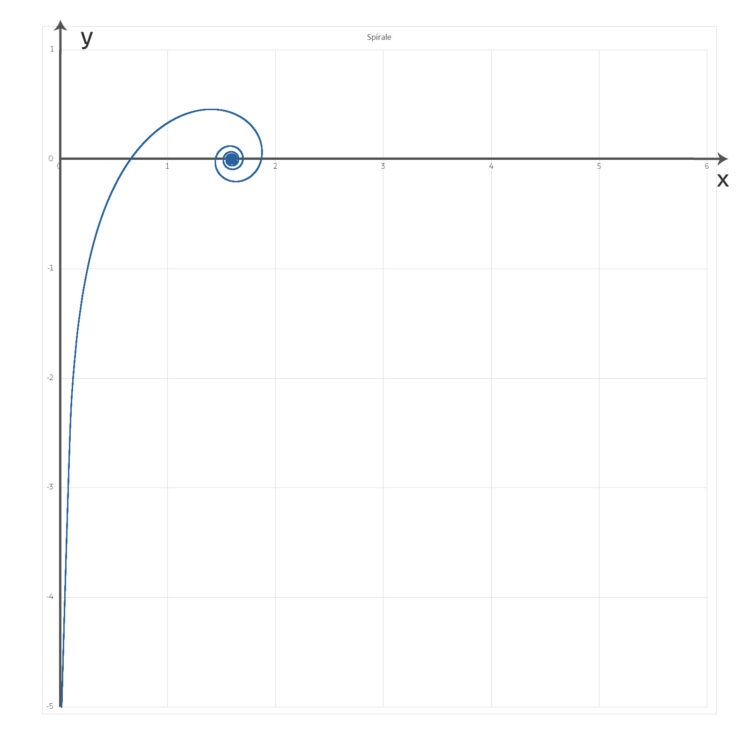
Lila Diese Kurve (x(T), y(T)) kann ich wieder zweidimensional zeichnen – mit einem kleinen Trick bei T = 0. Außerdem kann ich die Krümmung und die Bogenlänge ausrechnen.
Max Numerisch?
Besondere Eigenschaften der Spirale
Lila Nein, analytisch! Bogenlänge s von 0 bis T wird Unendlich, wie du dir denken kannst,
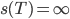
die Bogenlänge von einer positiven Zeit T0 bis T ist 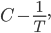 C ist eine geeignete Konstante, die ist jetzt nicht so wichtig:
C ist eine geeignete Konstante, die ist jetzt nicht so wichtig:
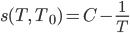
und die Krümmung K ist immer negativ, es ist
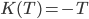
Siehst du, die Krümmung entlang der Spirale fällt linear mit der Zeit. Stell dir vor, du fährst mit der Zeit auf der Kurve entlang. Erst ist deine Neigung Null (am Anfang deiner Fahrt, im Punkt (0, - ∞) und dann neigst du dich immer mehr. Die Änderung der Krümmung geht aber so langsam, dass sie zumutbar ist, auch bei großen Lasten. Die Geometrie wird gern bei Track Transition Curves für Straßen oder Schienen benutzt.
Max Track Transition Curves? Ach, Übergangsbögen! Lila, dann sag mir doch, wo mein Auto starten soll, wo die Krümmung am kleinsten ist!
Lila Haha!
Übungsaufgaben
- Berechne den Grenzwert
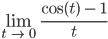
- Berechne die Bogenlänge s von T0 bis T, 0 < T0 < T, und insbesondere die Kontante C = C(T0).
- Kontrolliere die Krümmung K der Spirale in jedem Punkt T > 0.
Lösungen
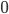
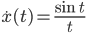
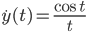
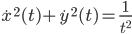

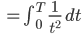
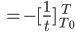
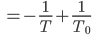
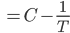
Also ist