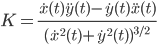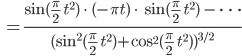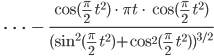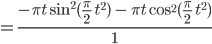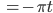Lila erzählt Max von weiteren Funktionen des Geologen und Erdbeben- und Nukleartestforschers von Seggern.
Lila Die letzte Funktion
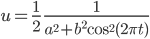
hat für a = 0 Polstellen. Wenn ich die Fläche von 0 bis zur 1. Polstelle berechne – die könnte ja für die Energie stehen, die bei einem solchen Erdbeben frei wird – so kommt leider unendlich raus. D.h. schon ein einziger Stoß von dieser Sorte setzt viel zu viel Energie frei. Ich find‘s jammerschade, dass die bis jetzt nicht konstruktiv genutzt werden kann, sondern nur destruktiv ist. Da wird mir beim Rechnen richtig unbehaglich.
Schwingungen quadratisch in der Zeit
Max Hmm. Was hast du noch gefunden?
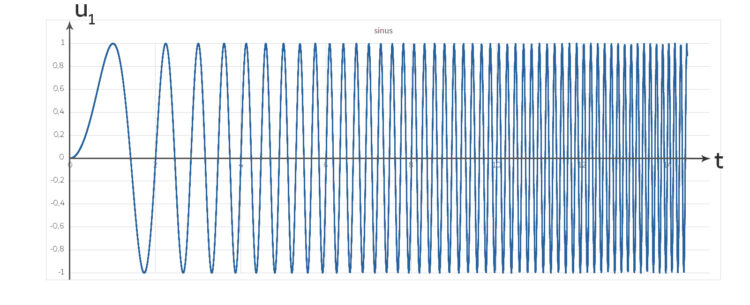
Lila Es gibt noch viele weitere Schwingungen – doch die hier, wo die Zeit quadratisch in den Sinus und Kosinus eingeht, finde ich ganz interessant:
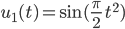
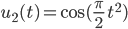
Wenn man dann noch die Funktionen u1 und u2 von 0 bis T integriert, kommt man auf die Fresnel-Integrale
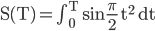
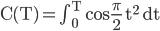
Fresnel-Integrale
Max Fresnel-Integrale?
Lila Ja. Diese Integrale kommen in der Optik vor. Man kann sie bei der Beugung von Licht am Spalt beobachten und dann das Fehlerintegral berechnen. Da bin ich leider 200 Jahre zu spät drauf gekommen, aber besser zu spät, als niemals. Jedenfalls hat Augustin Fresnel den Wellencharakter des Lichtes entdeckt und bei der mathematischen Formulierung sind diese Integrale aufgetreten. Deshalb heißen sie Fresnel-Integrale.
Ich fand sie mathematisch reizvoll. Es sind zwar transzendente Funktionen, das heißt, es gibt gar keine konstruktive Berechnungsvorschrift, aber mit einem lächerlichen Tabellenkalkulationsprogramm kann ich diese Integrale lösen und zeichnen. Dafür würde mich Kubicki schon wieder rausschmeißen!
Max Hey! Was berechnet denn dein lächerliches Tabellenkalkulationsprogramm, wenn die Integrale gar nicht zu berechnen sind?
Lila Naja, für die Sinus- und Kosinus-Funktion nehme ich eine intelligente Näherung des Tabellenkalkulationsprogramms, die Integration nähere ich durch die Summe:
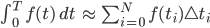
Max Haha! Dann ist Kubicki wohl ein Gegner von jeder digitalen Technik?
Lila Hmm, ich glaube schon. Aber ich nicht! Schau mal hier, das geht wirklich ganz schnell:
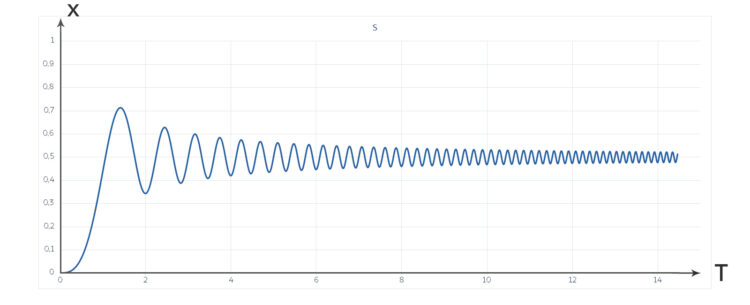
Fresnel-Integrale als Kurve in der Ebene
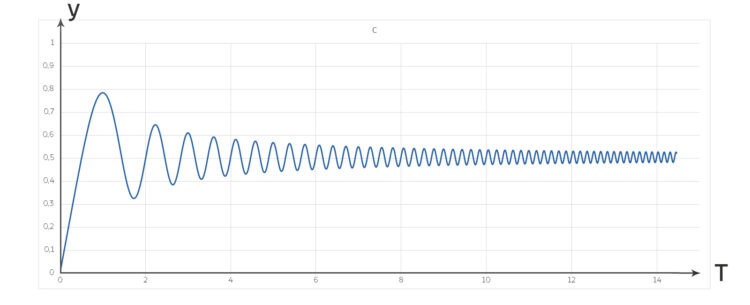
Wenn du nun zu jedem Zeitpunkt T die x- und y-Werte der Fresnel-Integrale zeichnest, erhältst du eine der schönsten Spiralen:
Max Hey, Lila! So was schaffst du?!
Fresnel-Integrale als Kurve im Raum
Lila Naja, von Seggern hat das auch schon gemacht. Aber schau mal, wenn ich die Spirale dreidimensional zeichne – dazu nehme ich für die 3. Koordinate die Zeit T multipliziert mit einer Konstanten – so kriege ich das:
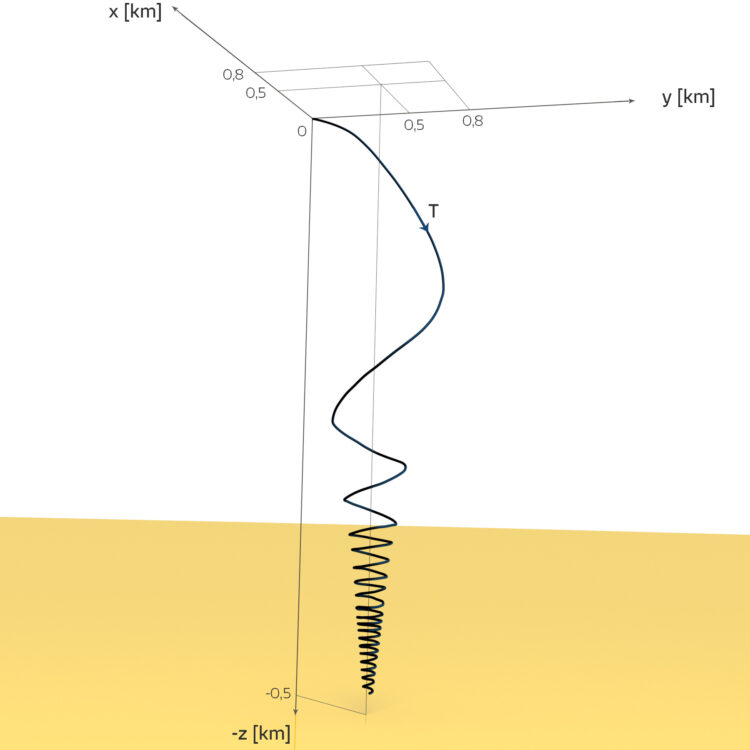
Max Lila, du hast gerade die Formel für einen Tornado gefunden!
***
Übungsaufgaben
Berechne Bogenlänge und Krümmung der Spirale!
Lösungen
1. Bogenlänge s von 0 bis T einer Kurve (x(t), y(t):

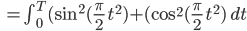
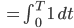
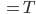
2. Krümmung K einer Kurve (x(t), y(t):