Ben und Rike bleiben am Nord-Ostsee-Kanal. Jetzt wollen sie sowieso nicht nach Berlin zurück. Sie bewundern die turbulente Strömung im Nord-Ostsee-Kanal hinter einem Schiff.
Ben Sag mal Rike, ergeben deine Navier-Stokes-Gleichungen auch Turbulenzen?
Rike Na klar, sie beschreiben das Verhalten von Flüssigkeiten, viskos oder nicht viskos, 2- oder 3-dimensional, mit und ohne äußere Anregungen. Turbulenzen sind experimentell gut untersucht, aber mathematisch ist das wirklich ein harter Brocken! Schon allein eine Formel für solche „turbulenten“ Funktionen zu finden, ist nicht so einfach.
Der Fourierreihenansatz
Ben Das Wasser scheint ja ziemlich herumzuwirbeln. Könnte man nicht einfach eine Fourierreihe als Lösung ansetzen:
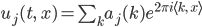
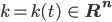
sind die Vektoren der Wellenzahlen. Dann könnte man über den Nord-Ostsee-Kanal integrieren, das wäre die Fouriertransformation der 
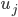’s, und dann könnte man die resultierenden Gleichungen für die Koeffizienten 
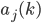lösen.
Rike ??? Sag mal, bist du ein Genie oder hast du die Arbeiten von Onsager und Isett gelesen?
Ben grinst.
Rike Na gut, dann weißt du ja auch, dass die Energie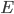 
einer Lösung durch
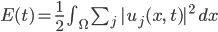
berechnet wird. Falls der Energieerhaltungssatz gilt, ist
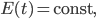
sonst wächst die Energie und die Entropie – und wir haben ein turbulentes Verhalten.
Ben Na klar.
Regularitätsverhalten schwacher Lösungen
Rike Dann weißt du wohl auch, dass man einer schwachen Lösung der Navier-Stokes-Gleichung an ihrem Regularitätsverhalten ansehen kann, ob sie dem Energieerhaltungssatz genügt oder nicht?
Ben Na ja, wie war das gleich: Wenn eine schwache Lösung 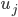die Ungleichungen
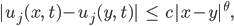
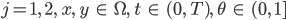
erfüllt, dann haben wir für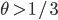 
die Energieerhaltung – und für 
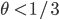eben nicht.
Rike Stimmt!
Ben Nur sind mir solche Funktionen bisher noch nicht begegnet.
Hölderstetigkeit – Beispiel
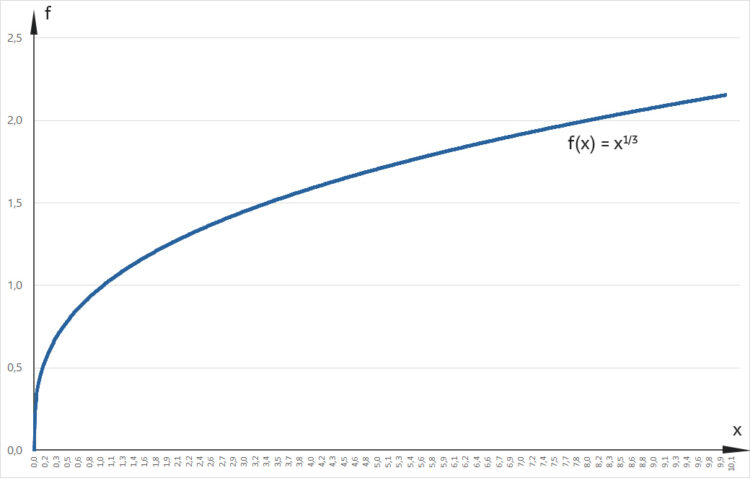
Rike Diese Eigenschaft aus der Ungleichung heißt Hölderstetigkeit,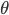 
ist der Exponent dazu, 
die Hölderkonstante. Nehmen wir mal die Funktion
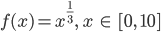
Dann kann ich gut diese Differenzen ausrechnen:
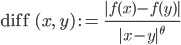
Ist
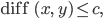
so ist die Funktion 
hölderstetig. Wegen
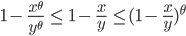
für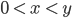 
und 
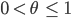ist
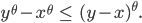
Wegen der Eigenschaften des Betrages kriegen wir daraus
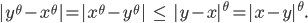
und folglich
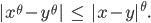
Die Hölderkonstante ist also 1:
.
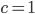Folglich ist
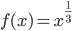
hölderstetig mit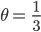 
. Außerdem kann man beweisen, dass auch hölderstetig mit einem Exponenten 
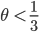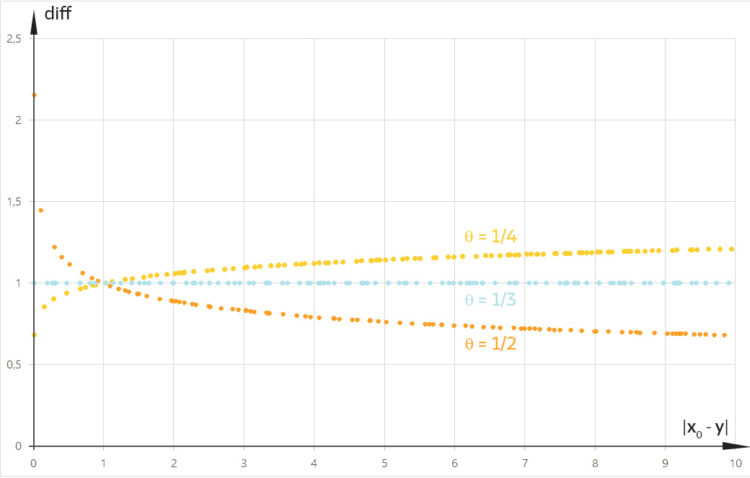
ist, aber nicht mit Exponenten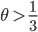 
. Ich kann versuchen, diese Differenz 
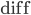zu berechnen, hier!
für 
mit verschiedenen 
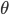. Für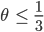 
ist die Differenz beschränkt.
Wenn ich mal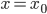 
nahe 0 festhalte, kriege ich für 
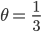die Differenz 
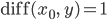für alle 
, die ich berechne. Bei 
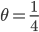bleibt die Differenz 
ebenfalls beschränkt, bei 
ist sie bei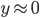 
unbeschränkt.
Ben Okay, verstehe… Das heißt, dass Funktionen der Art
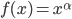
mit 
zu Turbulenzen führen können und mit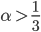 
eben nicht.
Rike Stimmt.
Ben Rike, hast du auch andere Beispiele?
Hölderstetigkeit – Gegenbeispiel
Rike Ja, nimm mal die Funktion :
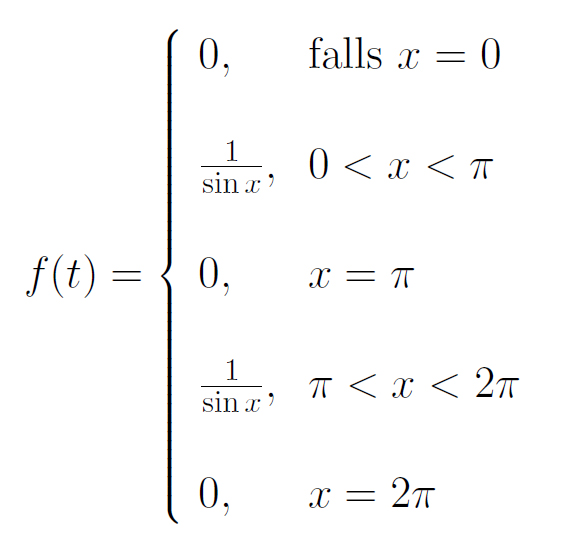
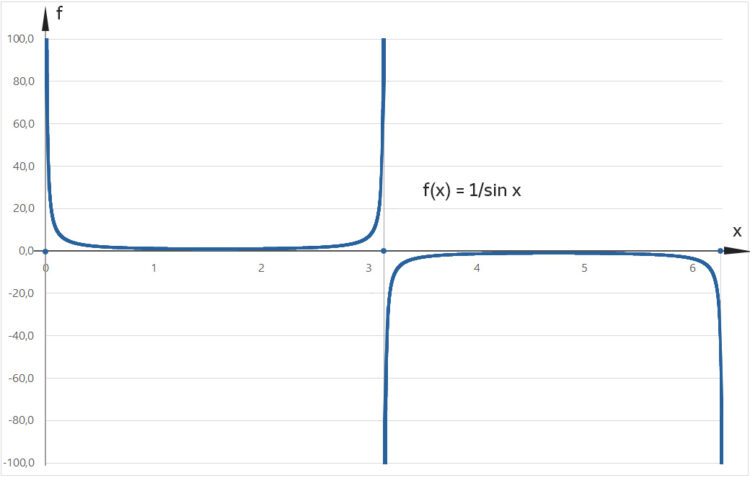
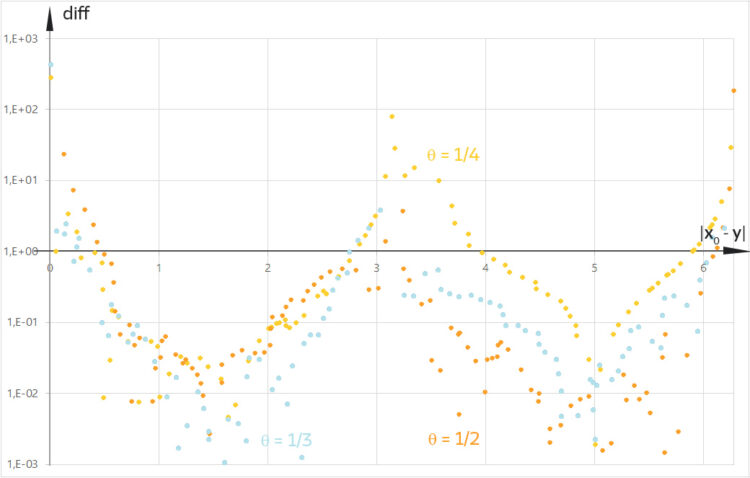
Die Funktion ist weder für 
noch für 
hölderstetig.
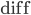für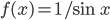 
und verschiedene .
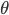Ben Ach, das sind echt unbequeme Funktionen, die können sich nur Mathematikerinnen ausdenken!
Rike Meinst du, Turbulenz ist fürn Apple und ‘nen Huawei zu haben?
Ben Nee, war nur ‘n Scherz.
Rike lacht.
***
Übungsaufgaben
- Wie könnte man die Differenzfunktion 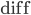für alle
und berechnen und darstellen? - Ist die Funktion des Gegenbeispiels für andere 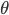hölderstetig?