Charly bereitet sich an einem Sonntagmorgen auf das nächste Schulhalbjahr vor und schaut sich die letzten Mathe-Abiaufgaben an. Die Analysis-Aufgabe zur Internationalen Gartenbauausstellung 2017 in Berlin hat es ihm besonders angetan.
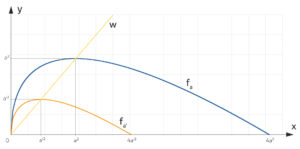
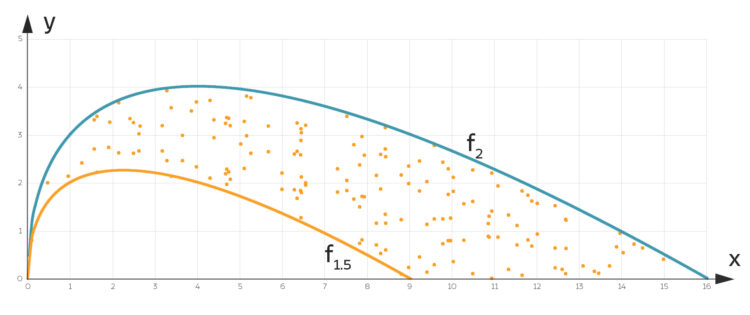
In dieser Aufgabe soll ein rechteckiges Beet (16 m x 6 m) durch Kurven der Form
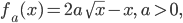
geteilt werden, siehe Abbildung.
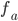. Abb. nach dem Original, Aufg. 1.1.Kurvendiskussion
Schnell berechnet er für die Teilaufgabe a):
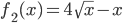
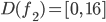
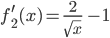
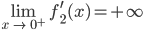
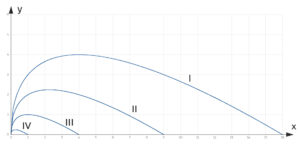
Für die Teilaufgabe b) erhält er wegen
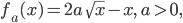
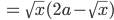
die Nullstellen
.
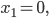
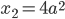Die „Hochpunkte“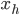 
liegen da, wo
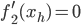
ist, also bei
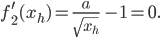
Das gilt genau dann, wenn
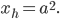
Wendepunkte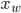 
liegen vor, wenn
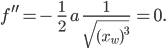
Aber das ist für
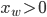
nicht möglich.
Parameter a der Kurven III und IV
Für die Aufgabe c) sollen die Parameter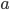 
der Kurven III und IV bestimmt werden sowie die Funktionsgleichungen angegeben werden. Auch das ist für Charly mit den nun berechneten Nullstellen nicht schwer:
Die Kurve III hat den Parameter
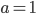
und es ist folglich
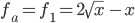
bzw. für die Kurve IV ist
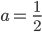
und es ist folglich
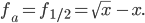
Ein Weg durch die „Hochpunkte“
Für die nächste Teilaufgabe d) soll ein Weg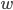 
durch die "Hochpunkte" gelegt werden.
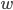durch die "Hochpunkte"Dieser Weg verläuft durch alle Punkte
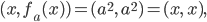
also ist
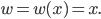
Flächenberechnung des Blumenbeetes
Jetzt kommt der für Charly interessanteste Teil e). Auf der Fläche zwischen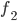 
und 
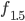sollen Blumen gepflanzt werden – und zwar 6 Blumen/m². Wie viele Blumen sollen bereitgestellt werden?
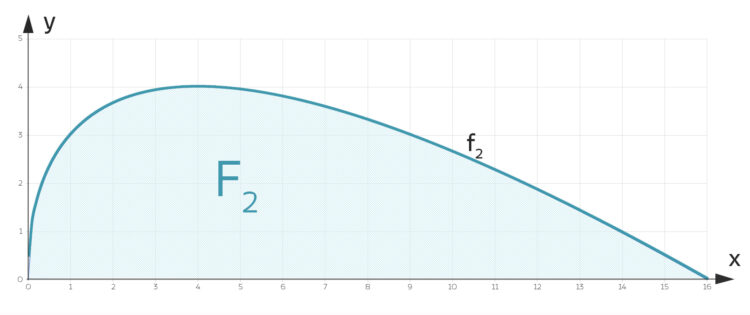
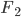
Charly berechnet die Fläche 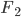zwischen 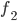und der 
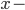Achse:
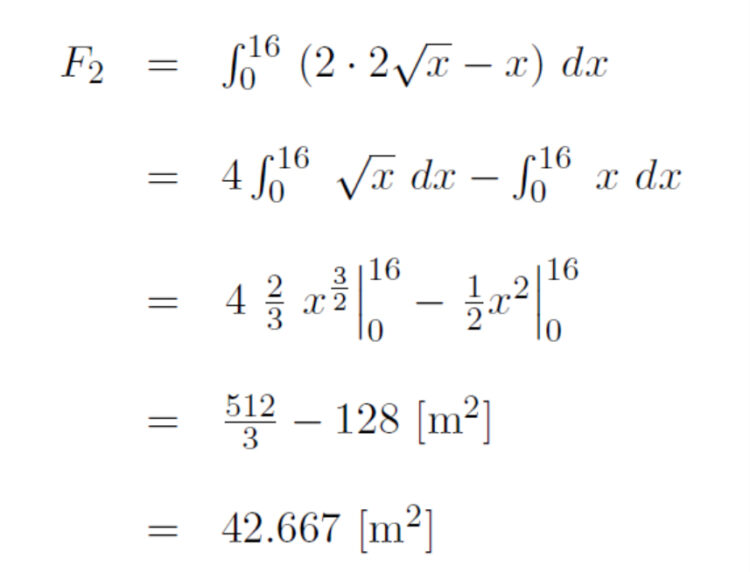
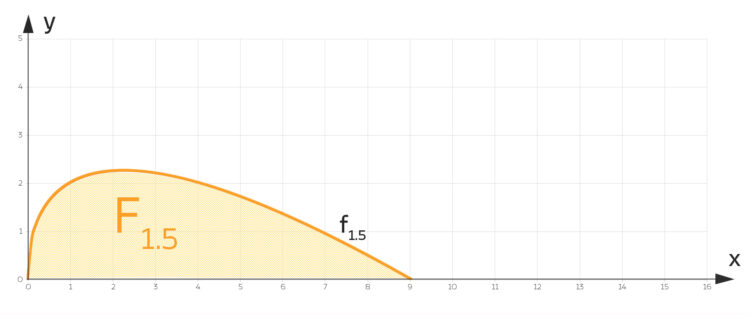
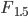
Für die Fläche 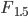zwischen und der 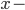Achse erhält er analog in m²:
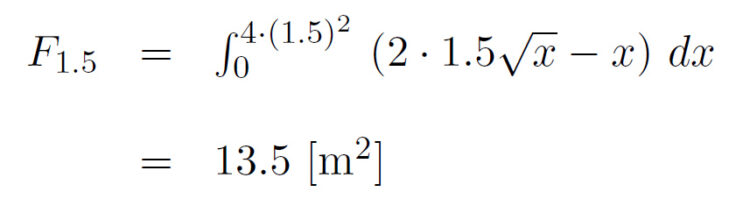
Die Fläche 
für die Blumen zwischen den beiden Kurven und ist also die Differenz zwischen den beiden Flächen 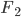und :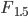
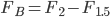
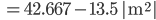
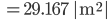
Blumen im Beet
Charly überlegt, wie er 6 Blumen auf 1 m² anordnen würde. Wären es 9 Blumen, könnte er ein regelmäßiges Muster bilden, doch mit 6 Blumen findet er keine Lösung für das Problem. Er zeichnet einen Entwurf. Vielleicht so?
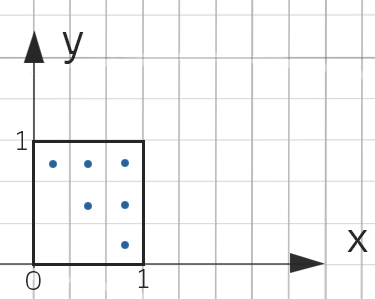
Da kommt Rike dazu und er fragt sie. Sie lacht sich kaputt über seinen Vorschlag.
Rike Da bleiben ja immerzu Lücken im Beet, das geht nicht!
Charly Okay, Rike. Wie würdest du das Beet bepflanzen?
Rike Hmm, die Aufgabensteller meinen sicher, dass im Mittel 6 Blumen pro Quadratmeter gepflanzt werden. Dann würde ich auf jeden Quadratmeter zufällig 6 Blumen pflanzen.
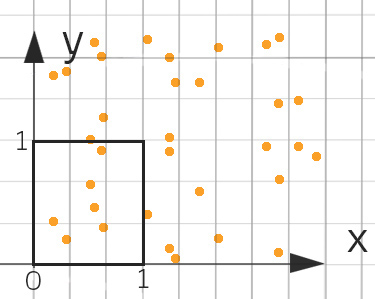
Charly Sag mal, bist du verrückt?
Rike Nö, wieso? Lass uns das mal versuchen! Ich berechne 6 Zufallszahlen für die x-Koordinate und 6 Zufallszahlen für die y-Koordinate. Das gibt im Mittel 6 Blumen und insgesamt ist dann die Anzahl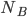
der Blumen im Beet
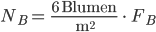
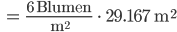
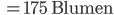
Charly Ja, das stimmt, im Mittel kriegst du 175 Blumen auf das Beet. Doch wie viele kriegst du wirklich ‘drauf? Kannst du mir ein paar Beispiele berechnen?
Rikes verschiedene zufällige Lösungen
Rike Ja, klar, mit einem Tabellenkalkulationsprogramm kann ich die Blumen verteilen und zählen, hier hast du verschiedene Varianten – natürlich immer mit 6 Blumen/m²:
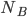= 166
= 175
= 185
Charly Mann, Rike! Das Ergebnis der Analysis-Aufgabe ist vom Zufall abhängig! Außerdem sieht nicht einmal die Lösung mit den 175 Blumen gut aus! Du hast ausgerechnet, dass es nicht ausreicht, 175 zu bestellen, besser wäre es, 185 zu bestellen. Rike, ich glaube, du hast die Aufgabe nicht richtig gelöst, jedenfalls nicht im Sinne der Aufgabensteller!
Rike Soso, ich habe die Aufgabe nicht richtig gelöst, sagt der Mathelehrer! Muss ich jetzt mein Abi zurückgeben?
Charly Nein, Rike, brauchst du nicht, ich glaube, du bist nicht für diese Welt mit diesen Abiaufgaben geschaffen.
Charly Aber du?
Charly Haha! Komm, Rike, wollen wir mal mit dem Fahrrad zur IGA fahren?
Rike Na, los!
***
Übungsaufgaben
- Woran liegt es, dass es verschiedene Ergebnisse gibt?
- Gibt es noch andere Möglichkeiten, Blumen anzuordnen?
Lösungen
- Das Ergebnis hängt von der Geometrie des Beetes ab,. Das Beet besteht leider nicht aus einer Vereinignung von 1 m x 1 m -Flächen.
- ja, siehe die Fortsetzung Rikes seriöse Lösung der IGA-Aufgabe