Max und Lila sind heute im Schnee unterwegs. Als sie einen Fuchs sehen, fällt Lila eine von den Krotofil-Vorlesungen ein. Ganz begeistert erzählt sie Max davon. Es geht um ein weiteres motivierendes Beispiel für Differenzialgleichungen: das Räuber-Beute-System nach Lotka-Volterra.
Das lineare Räuber-Beute-System
Lila Für dieses Räuber-Beute-System brauchst du 2 Veränderliche: Nehmen wir mal 
für die Anzahl der Beutetiere und 
für die Anzahl der Räuber, die die Beute fressen. Es soll ausreichend Nahrung für die Beutetiere vorhanden sein. Wenn beide Spezies nicht interagieren und du eine Wachstumsrate von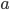 
für die Beute annimmst:
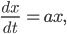
dann erhältst du ein exponentielles Wachstum:
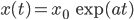
Max Okay! Exponentiell habe ich im letzten Jahr schon sehr oft gehört …
Lila Naja, das ist die Standardlösung für solche Aufgaben. Also weiter, wenn die Räuber der Beute nicht begegnen, und wenn diese Beutetiere ihr einziges Futter sind, dann würde ihre Population mit einem Faktor 
abnehmen:
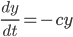
Die Lösung wäre dafür
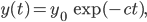
die Räuberpopulation würde sehr schnell aussterben.
Max Okay. Klar!
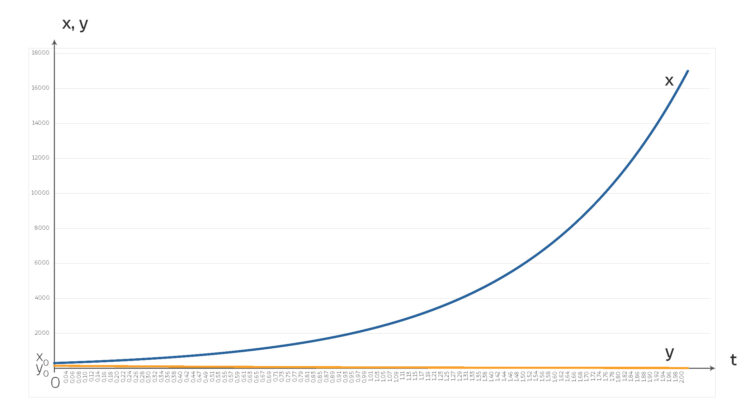
die Beute (blau), die Räuber (Orange)Das nichtlineare Räuber-Beute-SystemSystem
Lila Jetzt kommt die Interaktion dazu. Wie beim Epidemiemodell hängt dann die Änderung der beiden Populationen sowohl von als auch von ab – eben vom Produkt 
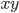, proportional zu und zu verringert sich die Beutepopulation und genauso vergrößert sich die Räuberpopulation. Hier lässt du jeweils einen unabhängigen Parameter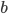 
bzw.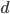 
zu und du erhältst das Lotka-Volterra-Modell:
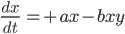
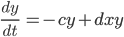
Max Na, gut! Bringt das nicht jede Menge Schwierigkeiten?
Lila Stimmt! Das ist ein System von nichtlinearen DGLn, die wir nicht exakt lösen können, aber Krotofil hat ihre Eigenschaften diskutiert. Ich habe das gleich numerisch getestet.
Fall mit sehr geringer Interaktion d = b = 0.001
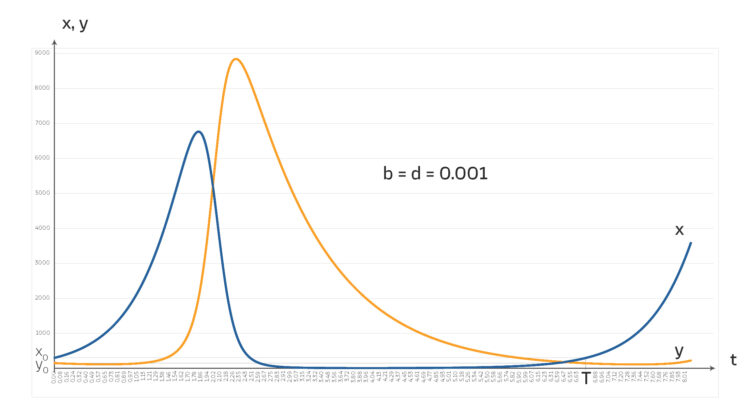
die Beute (blau), die Räuber (Orange), die Periode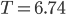 
Zeiteinheiten.Max Wow, jeder 1000.te Fuchs frisst einen Hasen in einer Zeiteinheit – pro Jahr? Aus 300 Hasen werden fast 7000 nach einem guten Jahr, dann fressen die Füchse fast alle auf und vermehren sich im nächsten Jahr zu fast 9000, das sind zu viele … hey, das gefällt mir! Stimmt das auch, was du ausrechnest?
Lila Ja, Krotofil hat uns vorgerechnet, dass es die Gleichgewichtslösungen
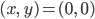
und
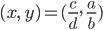
gibt. Für positive Parameter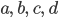 
und positive Anfangswerte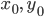 
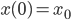
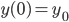
gibt es immer positive, periodische Lösungen, die im Phasenraum um die zweite Gleichgewichtslösung herum liegen. Ich habe das wieder mit Runge-Kutta gelöst. Schau mal, das sieht so aus:
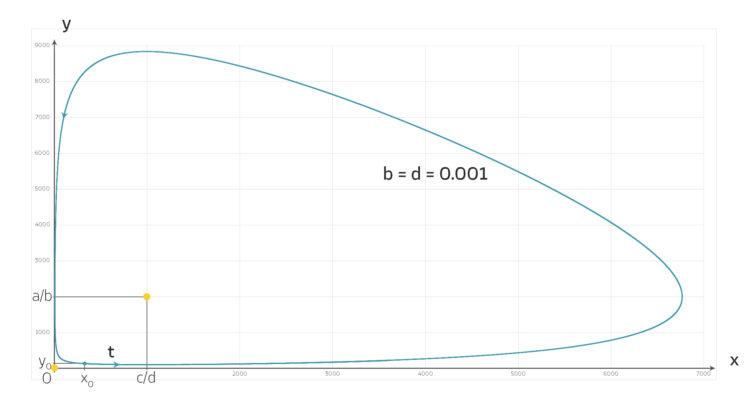
Max Hey, Lila, krass, hast du lange dafür gebraucht?
Lila Bei der geringen Interaktion musste ich viele Zeitschritte machen, um die periodische Lösung zu finden. Da habe ich schon ein bisschen Zeit gebraucht. Aber bei einer größeren Interaktivität ging das schon besser. Ich habe zwar heute den ersten Fuchs in Deutschland gesehen, doch jetzt kann ich mir sein Verhalten vorstellen. Der hat bestimmt einen "Interaktionsfaktor" von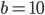 
!
Max Haha! Das denke ich auch!
Fall mit geringer Interaktion d = b = 0.01
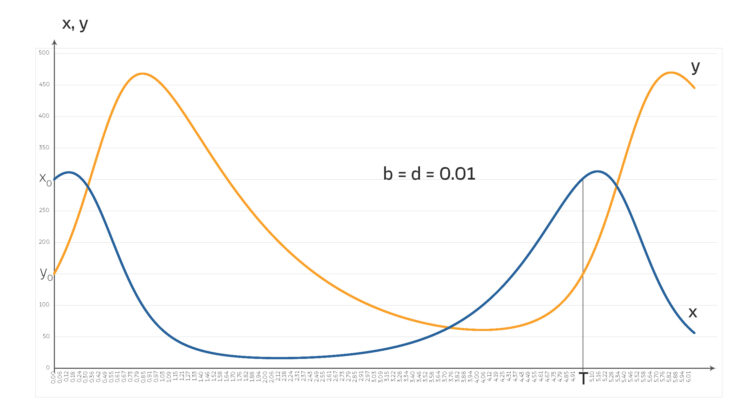
die Beute (blau), die Räuber (Orange), die Periode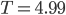 
Zeiteinheiten.
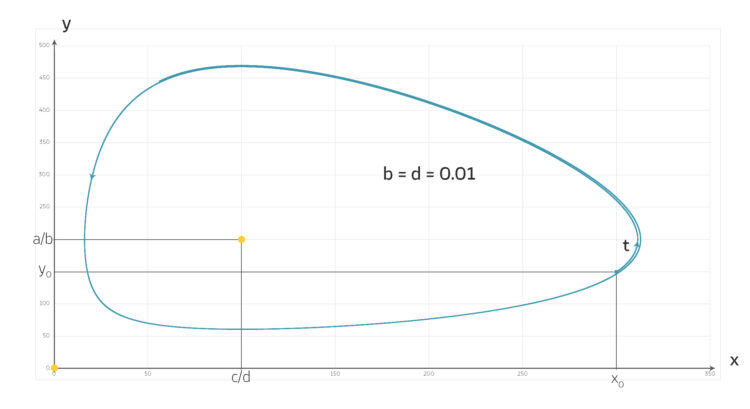
Lila Bei stärkerer Interaktion der Räuber- und Beutetiere verkürzt sich die Periode der Lösungen und meine numerischen Lösungen sind bis auf eine kleine Ungenauigkeit periodisch.
Max Lila, du bist genau richtig hier. Warum habe ich eigentlich nicht bei Anna Krotofil Mathe gehabt?
Lila Haha!
***
Übungsaufgaben
- Löse das im nichttrivialen Gleichgewicht linearisierte Lotka-Volterra-Modell!
- Berechne Lösungen für
!
Lösungen
- Das lineare System im Punkt
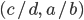heißt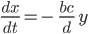
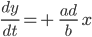
Die Lösungen dazu:
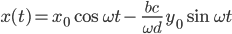
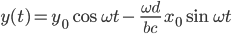
mit
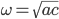
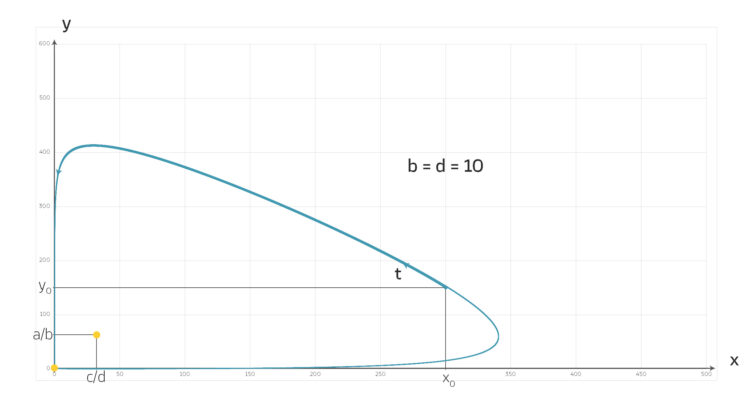
- Für bekommt Lila einige Schwierigkeiten und muss die Schrittweite für die Zeit stark verkleinern.
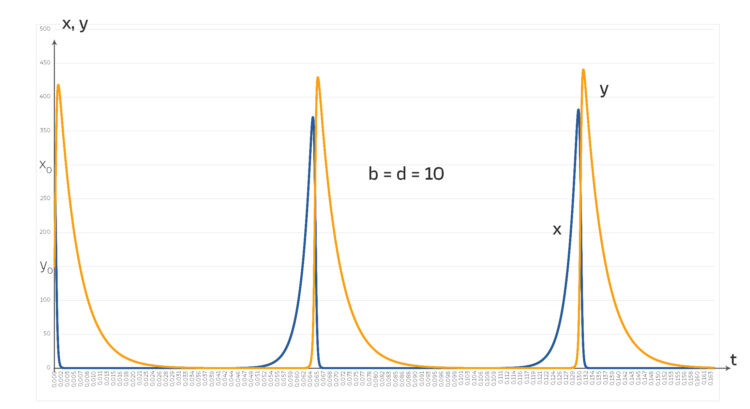
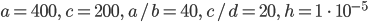, numerische Schwierigkeiten.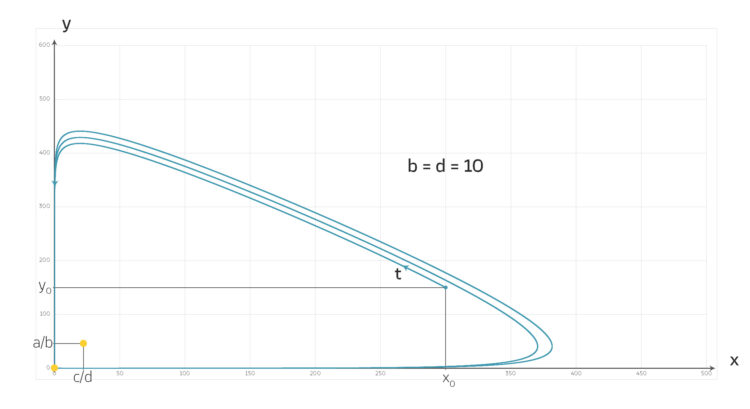
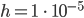und denselben Parametern wie oben.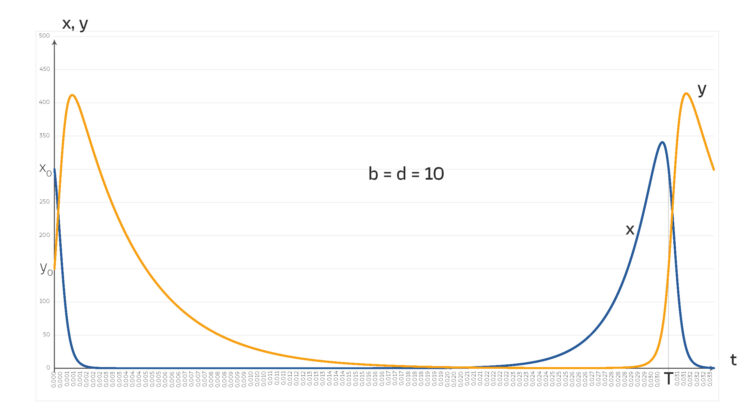
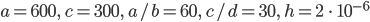
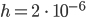und denselben Parametern wie oben.