Lila erzählt Max wieder von den Krotofil-Vorlesungen. Bevor sie die große Theorie behandelte, haben sie u.a. DGLn aus der Physik betrachtet.
Lila Überall, wo zeitliche Prozesse stattfinden, spielen DGLn eine große Rolle: wenn du mit dem Fahrrad fährst, mit dem Auto, wenn du kochst, wenn du dein Handy benutzt oder wenn sich die Planeten im All bewegen.
Max Und was hat dir daran gefallen?
Das Gravitationsgesetz für Planetenbahnen
Lila Du weißt ja bestimmt, dass die Planeten um die Sonne herumfliegen. Ihre Bahn wird durch die Gravitation bestimmt. Anna Krotofil hat eine 2-Körper-Aufgabe hergeleitet und in 2 Dimensionen exakt gelöst. Das hat mir gefallen.
Max Du siehst ja schon schlauer aus als Kepler! Ganz ohne Beobachtung?
Lila Hör‘ doch erst mal zu! Also die Gravitation kannst du zwischen 2 Körpern beschreiben durch die Gleichung:
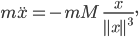
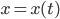 … zeitlich veränderliche Koordinaten des Planeten
… zeitlich veränderliche Koordinaten des Planeten
 … Masse des Planeten
… Masse des Planeten
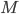 … Masse der Sonne,
… Masse der Sonne,
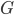 … Gravitationskonstante.
… Gravitationskonstante.
Skalierung des Modells
Die Entfernungen sind riesig, das Massenverhältnis 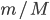 ist sehr klein, so wäre es besser, das System zu skalieren: statt in Metern in Relation zu astronomischen Einheiten, Astronomical Units (AU), statt in Sekunden in Relation zum Jahr und statt Kilogramm im Verhältnis zu
ist sehr klein, so wäre es besser, das System zu skalieren: statt in Metern in Relation zu astronomischen Einheiten, Astronomical Units (AU), statt in Sekunden in Relation zum Jahr und statt Kilogramm im Verhältnis zu 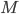 zu rechnen:
zu rechnen:
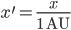
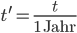
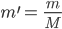
Dann haben wir dimensionslose Veränderliche. Aus der Gravitationskonstanten wird dann
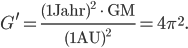
Max Wow, nicht schlecht!
Lila Die DGLn heißen dann
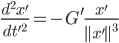
Max Gut. Dann kannst du die blöden Striche weglassen. Ich hasse sowas.
Lila Ich auch. Das 1. keplersche Gesetz sagt, dass diese Kurve 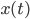 eine Ellipse ist. Ich habe mich gefragt: Wie kann man das beweisen? Es sind nichtlineare DGLn, nicht so ein einfaches System wie
eine Ellipse ist. Ich habe mich gefragt: Wie kann man das beweisen? Es sind nichtlineare DGLn, nicht so ein einfaches System wie
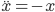
mit den Lösungen
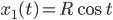
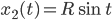
Max Okay, ich verstehe. Und wie geht es nun?
Lila Anna Krotofil hat gesagt, wir wissen ja, dass 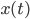 eine Ellipse ist, dann brauchen wir nur zu zeigen, dass solche Ellipsen Lösungen der DGLn sind.
eine Ellipse ist, dann brauchen wir nur zu zeigen, dass solche Ellipsen Lösungen der DGLn sind.
Max Aha!
Lila Zuerst legen wir geschickt eine Ebene durch die Bahnen, sodass wir die DGLn nur in einer Ebene zu lösen brauchen.
Max Aha! 2-dimensional!
Gleichungen der Planetenbahnen mit AWP
Lila Richtig! Die DGLn heißen dann:
Max Okay.
Lila Jetzt drehen wir das Koordinatensystem so, dass wir die Anfangswerte
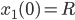
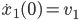
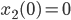
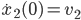
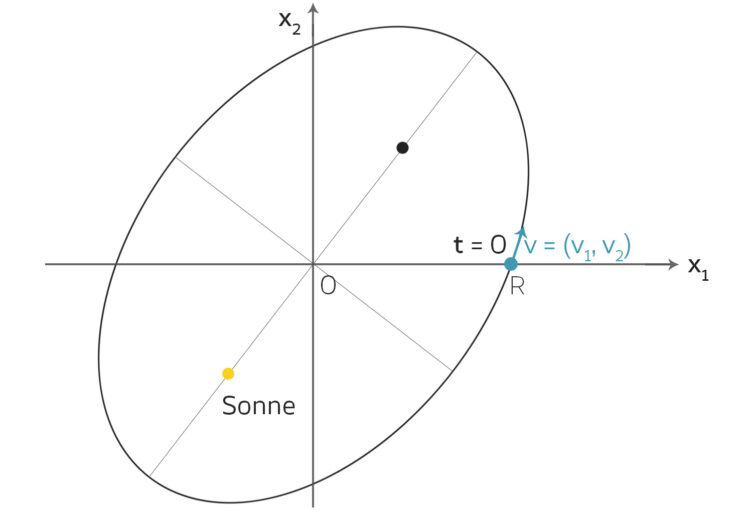
haben, mit 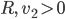 .
.
Max Okay.
Polarkoordinaten
Lila Jetzt hat sie Polarkoordinaten genommen, das heißt:
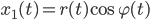
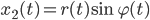
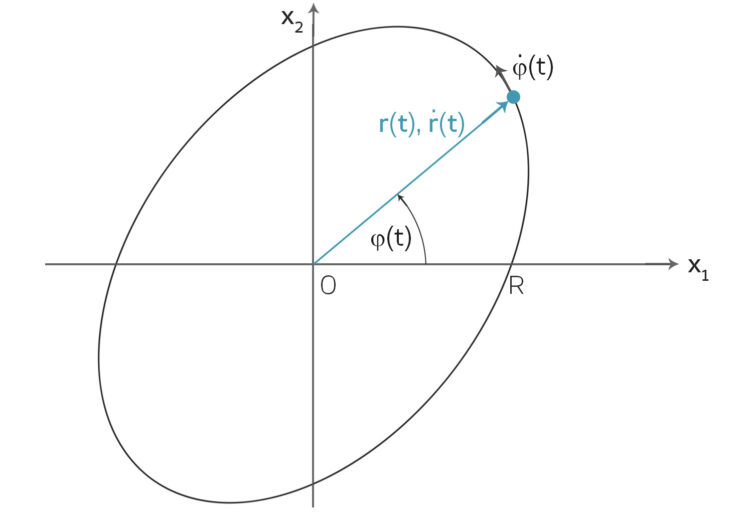
Die kannst du auch komplex schreiben:
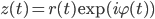
Wenn du das ableitest, kriegst du
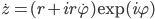
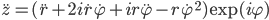
Aus
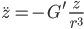
wird
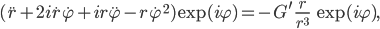
also
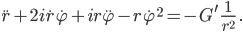
Planetenbahnengleichungen in Polarkoordianten und AWP
Das zerlegen wir in 2 Gleichungen, eine für den Realteil und eine für den Imaginärteil:
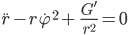
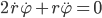
Die neuen Anfangsbedingungen sind dann:
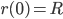
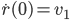
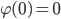
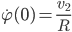
Max Mann! Okay! Alles a standard procedure?!
Der Ansatz
Lila Yes. Jetzt kommt ihre Idee – der Ansatz:
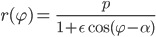
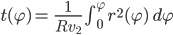
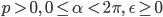 sind Parameter.
sind Parameter.
Max Wow! Wie kommt man darauf?
Lila Schau mal, der Ansatz ist gar nicht schlecht. Der Radius  variiert ein wenig in Abhängigkeit von
variiert ein wenig in Abhängigkeit von 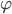 .
.
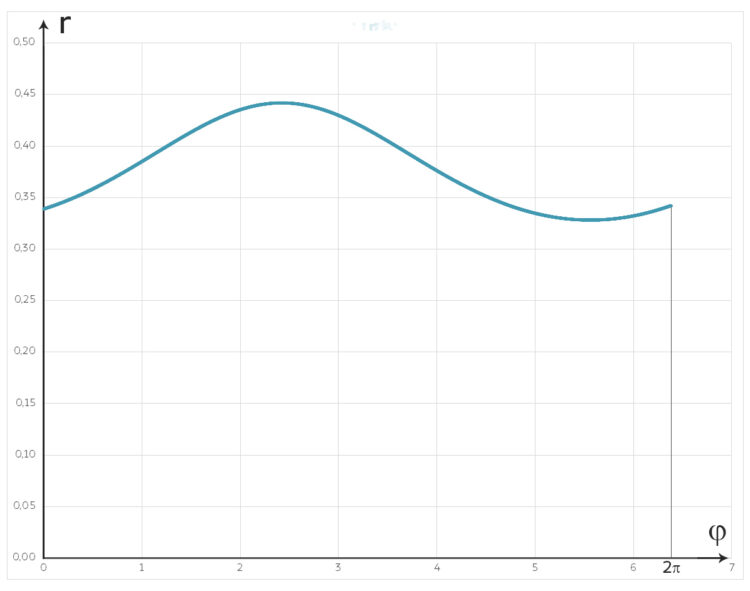
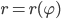 mit
mit 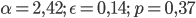
Max Ist der Ansatz nicht etwas komisch? Sollte sie nicht eine Funktion
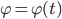
vorschlagen und nicht umgekehrt?
Diskussion der Parameter p, α und ε
Lila Stimmt! 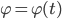 beschreibt den Winkel, den der Planet in Abhängigkeit von der Zeit durchläuft. Und
beschreibt den Winkel, den der Planet in Abhängigkeit von der Zeit durchläuft. Und
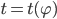
ist gerade die Umkehrfunktion, die Zeit in Abhängigkeit vom Winkel. Die Funktion konnte sie gut ableiten, in die DGLn einsetzen und dann hat das geklappt. Jedenfalls hat Anna Kratofil zwei Folien mit der Rechnung gezeigt. Sie hat beim Einsetzen des Ansatzes eine Gleichung für den Parameter 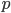 bekommen:
bekommen:
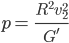
Wenn du den Ansatz für  in die Anfangsbedingungen
in die Anfangsbedingungen
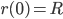
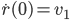
einsetzt, erhältst du
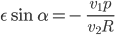
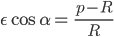
Das kannst du eindeutig auflösen und fertig ist die Theorie! Das ist das 1. keplersche Gesetz.
Max Hmm? Konntest du das denn auflösen?
Lila Ja, ich habe die beiden Gleichungen durcheinander geteilt und habe
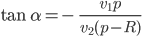
erhalten. Das kann ich nach  auflösen. Danach kann ich eine von den beiden Gleichungen nehmen und nach
auflösen. Danach kann ich eine von den beiden Gleichungen nehmen und nach 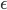 auflösen. Und so kann ich die Ellipse berechnen. Ich habe für den Merkur die Werte
auflösen. Und so kann ich die Ellipse berechnen. Ich habe für den Merkur die Werte
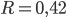
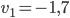
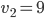
genommen und habe
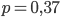
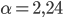
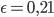
erhalten.
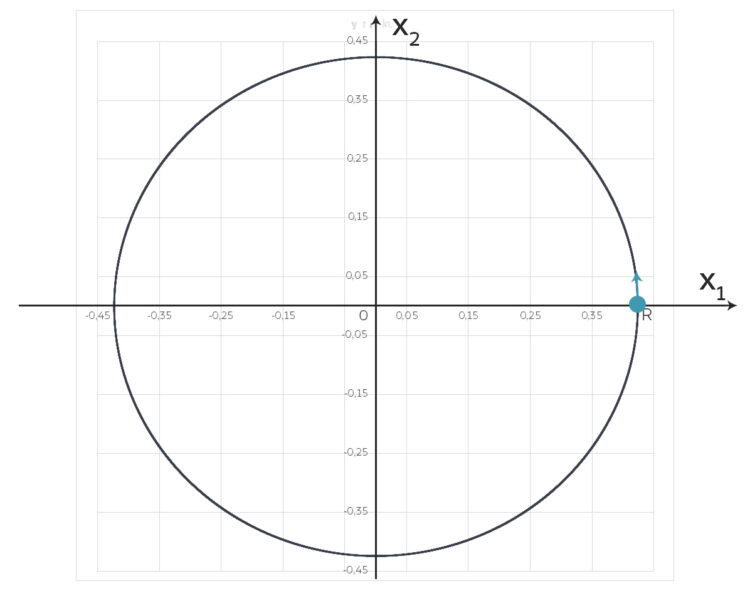
Verifizierung des Modells
Max Aber woher weißt du denn, ob das stimmt? Kannst du denn die beiden Halbachsen berechnen?
Lila Ja, das kann ich, die beiden Hauptachsen 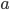 und
und 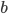 sind
sind
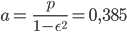
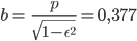
Max Geil! Das stimmt ja! Woher hast du eigentlich den Abstand 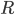 und die Geschwindigkeiten
und die Geschwindigkeiten 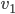 und
und 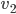 ?
?
Lila Haha! Das verrate ich nicht!
Übungsaufgabe
Versuche, für andere Planeten die Parameter 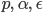 und schließlich die Ellipsenbahn dieses 2D-Modells zu bestimmen.
und schließlich die Ellipsenbahn dieses 2D-Modells zu bestimmen.