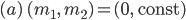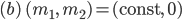Als Lila und Max zusammen kochen und essen, fällt Lila die Weihnachtsgeschichte von Anna Krotofil ein.
Lila Ein Ehepaar kocht und isst gerne zusammen. Beide haben immer großen Appetit. Je mehr sie kochen und je mehr sie essen, umso stärker wird ihr Appetit. Die Frau hat das Gewicht 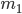 , der Mann das Gewicht
, der Mann das Gewicht 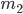 . Je mehr sie essen, umso mehr nehmen sie zu. Sie „feuern“ sich gegenseitig beim Kochen und Essen an. Deshalb ist die Gewichtszunahme bei beiden proportional zu jedem ihrer beiden Gewichte und also auch zum Produkt
. Je mehr sie essen, umso mehr nehmen sie zu. Sie „feuern“ sich gegenseitig beim Kochen und Essen an. Deshalb ist die Gewichtszunahme bei beiden proportional zu jedem ihrer beiden Gewichte und also auch zum Produkt 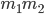 . Das Gewicht der Frau ändert sich genauso:
. Das Gewicht der Frau ändert sich genauso:
DGLn und Anfangswerte
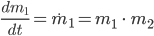
Das Gewicht des Mannes ändert sich viel weniger, es verändert sich nur zu einem kleinen Teil des Produktes:
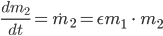
Die Anfangswerte sollen
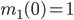
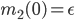
sein. Also, zu Beginn wiegt die Frau 100 kg und der Mann 50 kg, wenn wir 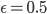 wählen. Dann hat uns Anna Krotofil die Lösung vorgerechnet. Das geht so:
wählen. Dann hat uns Anna Krotofil die Lösung vorgerechnet. Das geht so:
Lösung der nichtlinearen DGL
Du teilst die beiden Gleichungen durcheinander
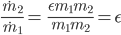
und schreibst dafür
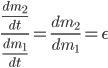
Dann fasst du 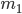 als Veränderliche auf und integrierst das:
als Veränderliche auf und integrierst das:
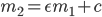
Max Das ist ja ziemlich trickreich!
Lila Yes, you are right. Dann setzt du die Anfangswerte ein und erhältst, dass die Integrationskonstante Null wird:
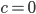
Max Okay.
Lila Also haben wir
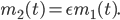
Max Okay. Der Mann wiegt immer halb so viel wie seine Frau.
Lila Yes. Das setzen wir in eine der DGLn ein, nehmen wir mal die erste:
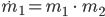
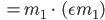
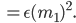
Methode der Trennung der Veränderlichen
Jetzt holen wir alle Terme mit 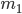 auf eine Seite und kriegen
auf eine Seite und kriegen
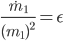
Das schreiben wir auch wieder geschickt mit dem Differentialkalkül
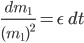
Jetzt können wir das integrieren. Auf der linken Seite ist 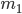 die Veränderliche und rechts die Zeit
die Veränderliche und rechts die Zeit 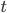 :
:
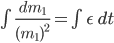
Das ergibt
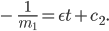
Den Term können wir nach 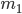 auflösen …
auflösen …
Max Ja, klar,
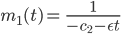
Lila Stimmt! Jetzt nehmen wir wieder den Anfangswert, um die Integrationskonstante zu bestimmen:
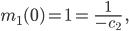
also ist
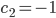
und
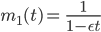
Max Okay, dann kriege ich auch das Gewicht des Mannes heraus:
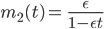
Unfalltod
Lila Right! Du siehst, solange der Nenner positiv ist,
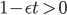

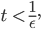
solange sind die Funktionen 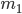 und
und 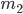 auch positiv. Wenn die Zeit nach
auch positiv. Wenn die Zeit nach
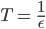
geht, dann „explodieren“ beide Funktionen:
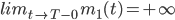
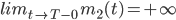
Max Beide essen sich zu Tode, die Frau platzt zuerst?
Lila Ja!
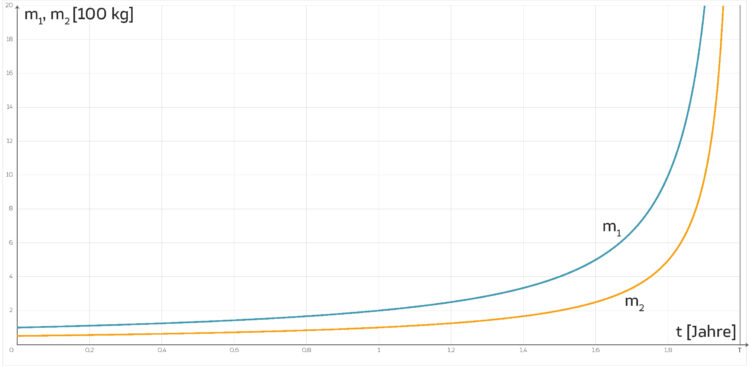
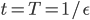
Das Interessante ist, dass das Wachstum anfangs sehr langsam geht, nach der halben Explosionszeit ist noch nicht viel passiert. Deshalb werden solche Systeme gerne für Unfälle genommen, out oft he blue – wie sagt ihr dazu?
Max Wie ein Blitz aus heiterem Himmel.
Lila Yes, wie ein Blitz aus heiterem Himmel ist das Unglück da!
***
Übungsaufgaben
- Bestimme die nichtnegativen Gleichgewichtszustände der DGLn!
- Zeichne den Phasenfluss für positive
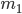 und
und 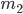 !
!