Lila bereitet sich auf ihre Prüfung vor. Sie arbeitet die Krotofil-Vorlesungen nach. Doch bei einem Problem kommt sie nicht weiter. Sie ist ganz verzweifelt.
Max Was ist denn los?
Lila Ich habe hier so ein Problem, da komme ich nicht weiter! Beim Unfalltod in der Küche ist die Lösung nach endlicher Zeit explodiert, und jetzt sitze ich an einem anderen Phänomen, nämlich dass die Lösung kollabiert. So ein Beispiel will ich numerisch lösen, aber ich kriege es nicht hin.
Max Was heißt kollabiert?
Lila Der Zustand  , den wir beschreiben, hört nach endlicher Zeit auf zu existieren.
, den wir beschreiben, hört nach endlicher Zeit auf zu existieren.
Max Aha!
Lila Stell dir vor, du hast ein Objekt; und das ändert seinen Zustand nach dem Gesetz:
Die „inverse“ Schwingungsaufgabe
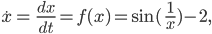
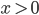
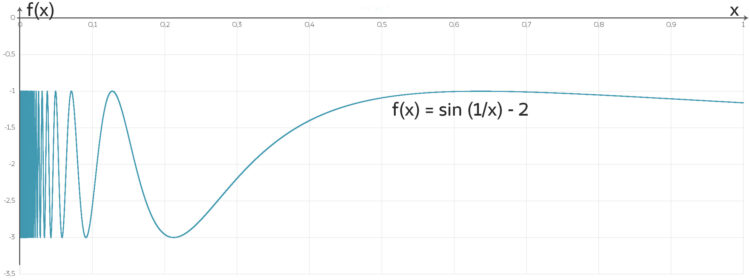
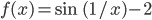 im Intervall (0, 1]
im Intervall (0, 1]Max Hmm, das ist ja eine komische Schwingung!
Lila Na, das ist die ganz normale Sinusschwingung, nur die Veränderlichen werden invertiert, aus großen Werten werden kleine, aus kleinen werden große, bei 1 ist alles unverändert.
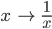
Max Sowas macht ihr an der Uni? Ihr tauscht Mikro- und Makrokosmos?
Lila Haha, ja, so ungefähr. Außerdem gibt es noch eine additive Konstante.
Max Na gut, 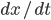 das die Änderung meines Gewichtes? Oder ist das die Änderung meines Kontostandes oder ist das die Geschwindigkeit meines Rollers?
das die Änderung meines Gewichtes? Oder ist das die Änderung meines Kontostandes oder ist das die Geschwindigkeit meines Rollers?
Lila Ja, das sind tolle Beispiele! Der Anfangswert soll sein:
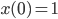
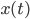 soll den Zustand eines Objektes beschreiben; seine Änderung ist durch diese „inverse Sinusschwingung“ erklärt. Doch je kleiner
soll den Zustand eines Objektes beschreiben; seine Änderung ist durch diese „inverse Sinusschwingung“ erklärt. Doch je kleiner  wird, umso schwieriger wird die Änderung, sie schwingt und schwingt. Wenn ich die Zeitachse in gleichgroße Schritte einteile und das numerisch integriere – wie ich das immer mache – mit der Runge-Kutta-Methode, dann überspringe ich die Stelle, wo
wird, umso schwieriger wird die Änderung, sie schwingt und schwingt. Wenn ich die Zeitachse in gleichgroße Schritte einteile und das numerisch integriere – wie ich das immer mache – mit der Runge-Kutta-Methode, dann überspringe ich die Stelle, wo 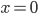 wird und bin plötzlich im Negativen. Schau mal hier: Wir haben die Anfangswertaufgabe
wird und bin plötzlich im Negativen. Schau mal hier: Wir haben die Anfangswertaufgabe
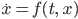
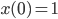
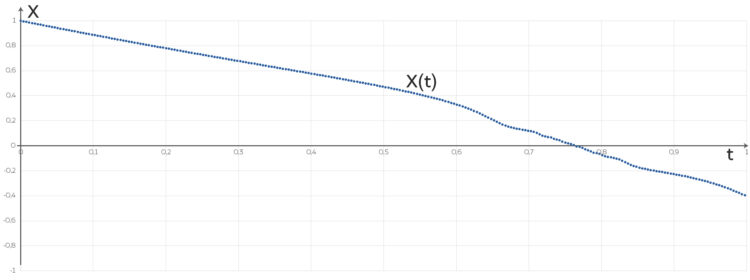
und 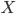 soll ihre numerische Lösung sein.
soll ihre numerische Lösung sein.
Max Wenn 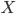 oder
oder  der zurückgelegte Weg mit meinem Roller ist, dann fahre ich quasi zurück – nach Hause? Und werde immer langsamer? Meine Geschwindigkeit geht kurz vorm Ankommen hoch und runter – wie verrückt?Solche Sachen berechnet ihr an der Uni?
der zurückgelegte Weg mit meinem Roller ist, dann fahre ich quasi zurück – nach Hause? Und werde immer langsamer? Meine Geschwindigkeit geht kurz vorm Ankommen hoch und runter – wie verrückt?Solche Sachen berechnet ihr an der Uni?
Lila Haha, ja, es ist wie ein Mikrostottern im Motor. Und ich bin bei meinem ersten Versuch durch dein Haus mitten durchgefahren.
Max Okay, verstehe! Dann musst du mir jetzt nur noch die Runge-Kutta-Methode erklären.
Euler-Vorwärts-Methode
Lila Die Runge-Kutta-Methode ist eine intelligente Einschrittmethode. Einschrittmethode bedeutet, dass ich mit einem Schritt von einem Zeitpunkt tn zum nächsten Zeitpunkt 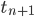 komme. Das einfachste Verfahren dieser Art ist das Eulerverfahren. Wenn wir eine Schrittweite
komme. Das einfachste Verfahren dieser Art ist das Eulerverfahren. Wenn wir eine Schrittweite 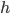 von einen zum nächsten Zeitschritt benutzen:
von einen zum nächsten Zeitschritt benutzen:
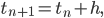
und die Zustände mit Xn bezeichnen
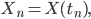
dann können wir die DGL vorwärts diskretisieren:
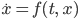
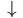
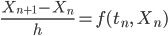
Das kannst du prima nach Xn+1 auflösen!
Max Jawoll, das kann ich:
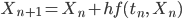
Lila Stimmt! Geometrisch bedeutet das, dass wir vom Anfangswert Schritt für Schritt mit dem Anstieg 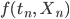 weitergehen.
weitergehen.
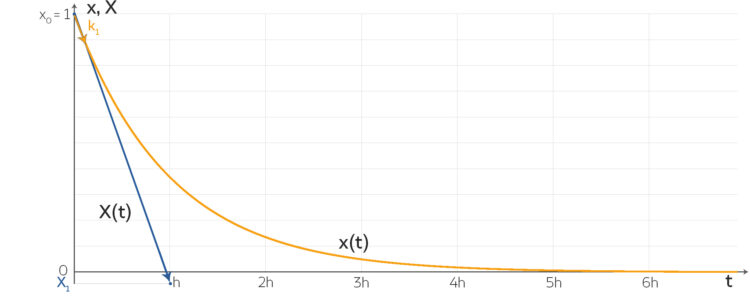
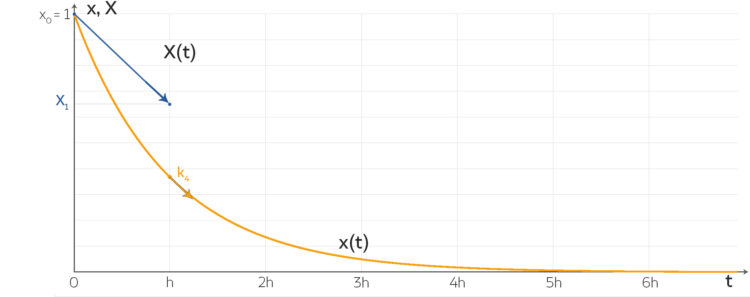
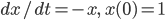 mit der Lösung
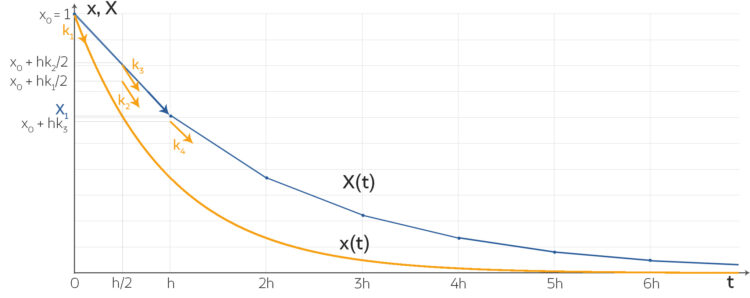
mit der Lösung  lassen sich numerische Methoden gut analysieren. Lilas geometrische Interpretation für diese lineare DGL mit der Euler-Vorwärts-Methode und dem Anstieg
lassen sich numerische Methoden gut analysieren. Lilas geometrische Interpretation für diese lineare DGL mit der Euler-Vorwärts-Methode und dem Anstieg 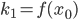 .
.Max Aha! Aber wenn deine Schritte zu groß sind, geht das schief!
Euler-Rückwärts-Methode
Lila Yes! Besser wäre die rückwärtige Diskretisierung:
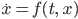
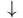
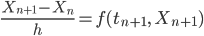
Wenn die Funktion  nichtlinear ist, so wie bei unseren Schwingungen, brauchen wir noch ein Verfahren, um die Gleichung
nichtlinear ist, so wie bei unseren Schwingungen, brauchen wir noch ein Verfahren, um die Gleichung
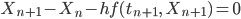
nach Xn+1 aufzulösen.
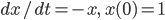 mit dem Anstieg
mit dem Anstieg 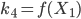
Max Aha! Numerische Nullstellensuche? Hmm. Und das immer wieder?
Runge-Kutta-Methode
Lila Genau! Ein großer Aufwand. Doch das Runge-Kutta-Verfahren berechnet 4 verschiedene Anstiege:
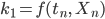
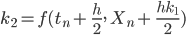
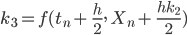
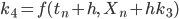
Die numerische Lösung wird dann aus diesen 4 Anstiegen in einem Schritt gemittelt:
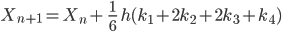
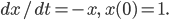
Max Okay, hört sich vernünftig an. Du kannst das programmieren?
Die numerische Lösung der „inversen“ Schwingung
Lila Ja, bis jetzt jedenfalls. Aber nun ist es passiert, dass sich bei einem Zeitschritt von tn nach 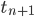 das Vorzeichen der Lösung geändert hat:
das Vorzeichen der Lösung geändert hat:


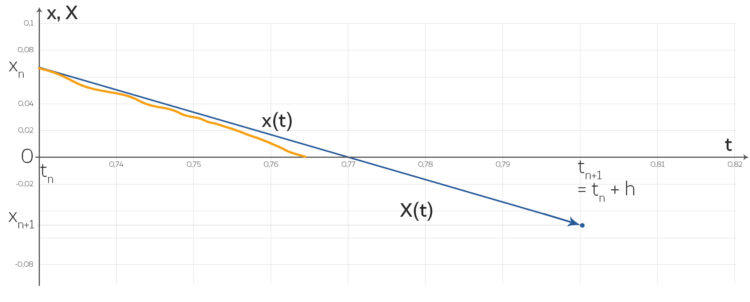
Max Dann mach doch deine Schritte kleiner!
Lila Ja, je kleiner ich sie mache, umso mehr Schritte muss ich machen und das Problem bleibt bestehen, früher oder später springe ich mit einem kleinen Schritt über die Null hinaus!
Max Hmm, kannst du nicht bei jedem Schritt testen, ob der nächste Wert negativ wird? Und dann deinen Schritt so klein machen, bis das nicht mehr passiert?
Lila Max, das ist eine tolle Idee! Es ist dann zwar kein Standardverfahren mehr, aber das müsste klappen!
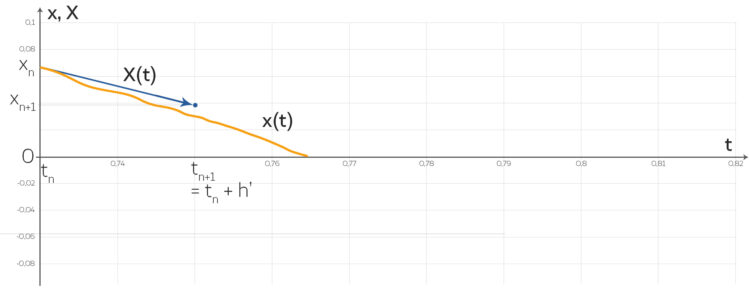
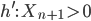
Jetzt muss ich nur noch die Zeit 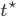 bis zum Kollaps berechnen…
bis zum Kollaps berechnen…
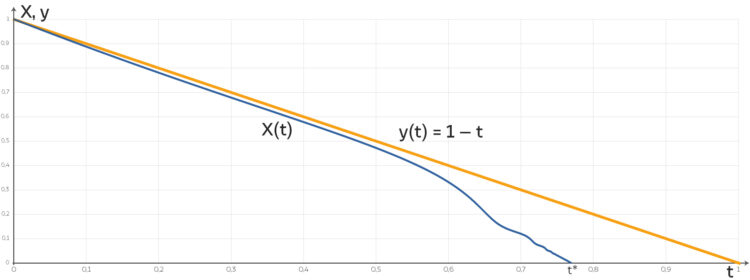
Max Ja mach das, ich teste das dann!
Übungsaufgaben
- Berechne t*!
- Begründe die obere Grenze von
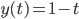
für die Lösung
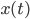 .
.
Lösungen
- 0,76935
- Aus der DGL folgt
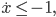
Nach Integration
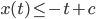
und mit dem AW
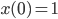
ergibt sich