Als Lila in ihrer Prüfungsvorbereitung für das Fach Gewöhnliche Differenzialgleichungen zur Methode der Trennung der Veränderlichen kommt, fällt ihr auf, dass sie die Aufgabe über die „inversen“ Schwingungen auch damit lösen könnte. Doch eine Schwierigkeit ergibt die nächste. Bloß gut, dass sie Jenny fragen kann, denn Jenny studiert auch Mathe und ist im letzten Semester.
Lila Hi, Jenny, ich bin bei Anna Krotofil an die Aufgabe
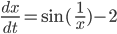
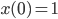
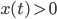
geraten. Als ich in die Nähe von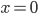 
kam, musste ich immer kleinere Schritte machen, quasi eine Schrittweitensteuerung einbauen. Ich hab‘s wieder mit Runge-Kutta gelöst, das ging ganz gut. So habe ich numerisch herausgefunden, dass die Lösung x bei
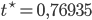
kollabiert.
Jenny Okay! Ich hatte in meiner DGL-Vorlesung nur analytisch lösbare Beispiele. Wir hatten nicht bei Krotofil. Aber was ist dein Problem?
Trennung der Veränderlichen
Lila Jetzt bin ich bei der Methode der Trennung der Veränderlichen angekommen und wende die mal auf mein Problem an, hier:
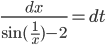
Jetzt integriere ich das, ich starte beim Anfangswert
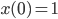
und ende beim Kollaps
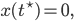
das ergibt
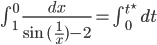
Jenny Okay, die rechte Seite können wir lösen, das ist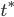 
. Bei der linken Seite integrierst du von rechts nach links? Wollen wir nicht die Grenzen tauschen?
Lila Na gut, dann haben wir
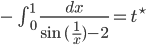
Die Probleme des Integranden
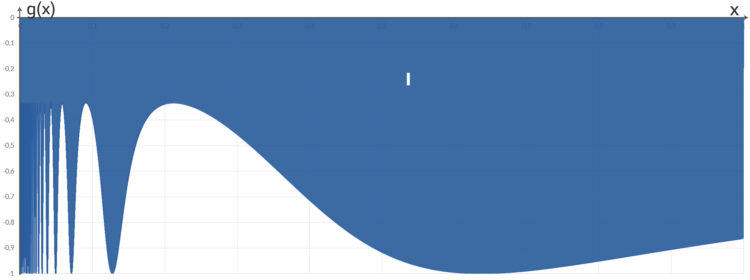
Jetzt brauche ich nur noch das Integral zu lösen. Aber weißt du, der Integrand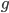 
:
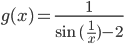
ist nicht stetig bei Null, da gibt es keine Integrationsmethode! Alle fordern stetige Integranden.
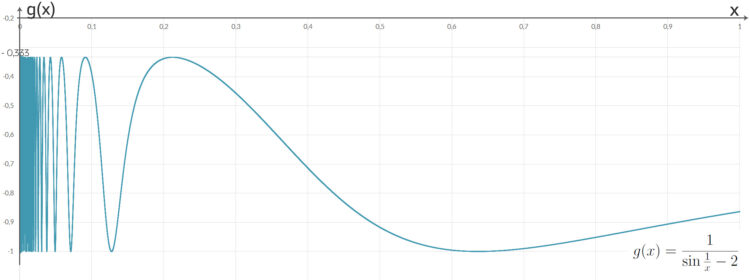
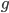, die in 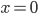keinen Grenzwert hat und die integriert werden soll
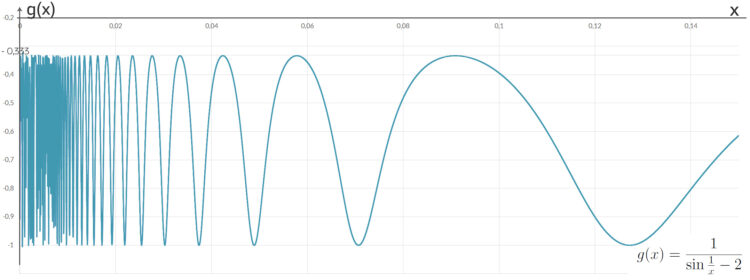
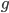
. Er zeigt die numerischen Probleme, zu berechnen.
Jenny Ja, Lila, der Integrand ist nicht stetig, also ist das Integral nicht Riemann-integrierbar. Es gibt keinen gemeinsamen Grenzwert der Ober- und Untersummen, du kannst die Zerlegungen so fein machen wie du willst. Du musst es als uneigentliches Integral auffassen.
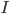
Das uneigentliche Integral
Lila Okay, das haben wir schon gehabt. Wir müssen überlegen, ob der Grenzwert der Integrale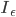 
:
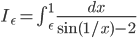
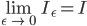
endlich bleibt.
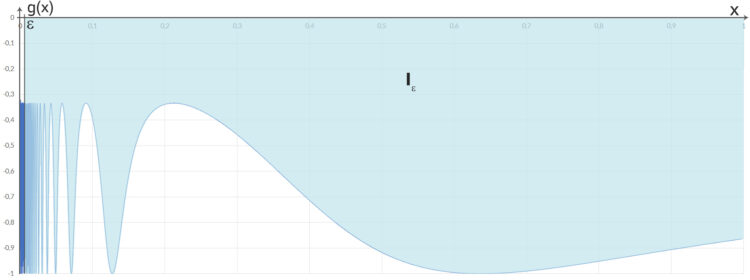
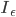
Jenny Wenn ich mir deine Funktion 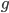so anschaue, dann fällt mir auf, dass die Folge der Teilintegrale 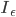von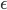 
bis 1 immer kleiner wird, die Integrale sind ja negativ!!!
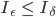
für
.
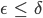Außerdem kannst du alle Teilintegrale durch Rechteckflächen abschätzen:
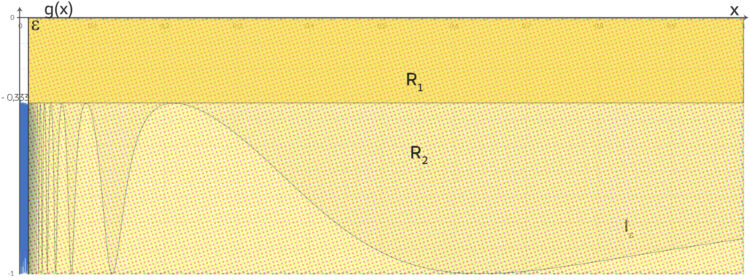
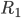liegt innerhalb 
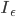und das große Rechteck R2 umschließt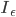 
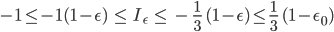
Das heißt, die 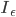bilden eine monoton fallende und beschränkte Zahlenfolge …
Lilas Trapeznäherung
Lila Super, dann haben sie auch einen Grenzwert! Ich kann jedes Teilintegral 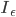durch die Summe von Trapezen 
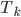beliebig genau nähern:
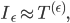
wobei
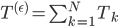
Dafür zerlege ich das Intervall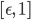 
mit 
Punkten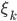 
– nach links hin immer feiner werdend. Jedes 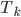berechnet sich nach der Trapezformel:
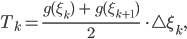
und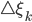 
ist meine Schrittweite:
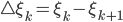
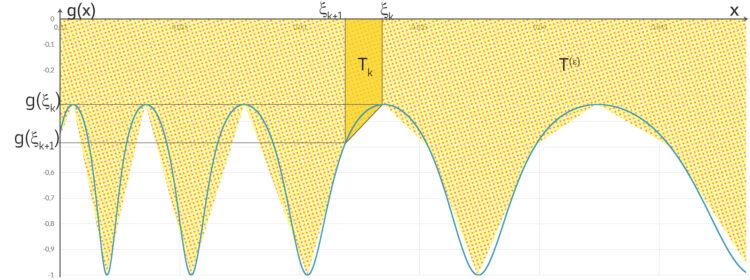
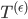(hier im Ausschnitt) ist die Näherung zum Integral 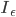.Jenny Hört sich gut an.
Lila Dann sollten meine Trapezsummen konvergieren, wenn die Abstände der 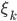immer kleiner werden:
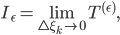
und wenn außerdem der linke Rand nach Null geht:
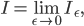
dann habe ich das Integral gelöst!
Jenny Aaah, gleich 2 Grenzwerte!!!
Lila Du kannst bestimmt beweisen, das das korrekt ist.
Jenny Hmm, du hast mir aber erklärt, dass du numerisch gar nicht den Limes machen kannst ….
Lila Yes, 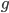ist für 
nahe 10-5 nicht mehr genau, because the Sinus function is hard to calculate, du siehst die Ungenauigkeiten in der Grafik.
Jenny Okay! Ich sehe es.
Lila Deshalb ist es sinnlos, die Schrittweiten noch weiter zu verkleinern. Das heißt, ich kann nicht beliebig genau nach Null gehen. Ich berechne also nur endlich viele Trapeze und mache no Limes, ich teste, wie viel die Summe der 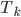von 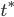abweicht. Wenn mein „Grenzwert“ auf ein paar Stellen nach dem Komma stimmt, wäre ich schon zufrieden.
Jenny Und hast du's geschafft, Lila? Naaaaa???
Lila Warte mal… ruf mich in einer halben Stunde noch mal an!
***
Übungsaufgaben
Versuche, das Integral numerisch zu bestimmen!