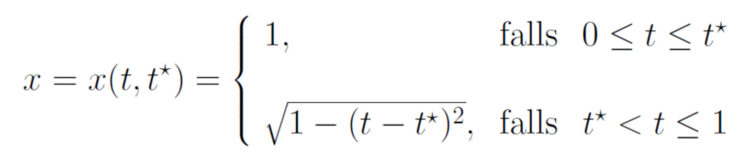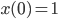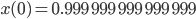Lila hat endlich ihre DGL-Prüfung bestanden und erzählt Jenny davon. Sie ist von ihrer Professorin Anna Kratofil zu nicht eindeutigen Lösungen gefragt worden.
Jenny Hi, Lila! Na, wie wars?
Die Anfangswertaufgabe
Lila Hi, Jenny, nice to see you. Ich habe die Anfangswertaufgabe (AWA)
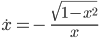
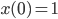
bekommen. Ich habe das gleich numerisch probiert und bin beim Anfangswert
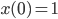
gestartet. Aber leider waren meine Increments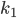 
bis 
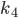immer Null, I couldn’t leave it! Ich bekam immer nur die konstante Lösung
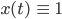
heraus. Ich war ganz verzweifelt. Das ist natürlich eine Lösung…
Jenny Und dann?
Lila Ich saß virtually in der stationären Lösung drin und kam nicht heraus. Und gleichzeitig war die stationäre Lösung der Anfangswert.
Jenny O, Lila! Ich glaube ich kenne das Gefühl, als wenn du in einer S-Bahn an der Endhaltestelle bist – und die Türen gehen nicht auf.
Lila Haha!
Jenny Oder wenn du deinen Lieblingssong in der Schleife hörst und nicht aufhören kannst…
Lila Haha. Oder wie beim Kuss, wenn Max nicht aufhören will?
Jenny Ja, genau!
Lila Dann habe ich die rechte Seite gezeichnet, hier:
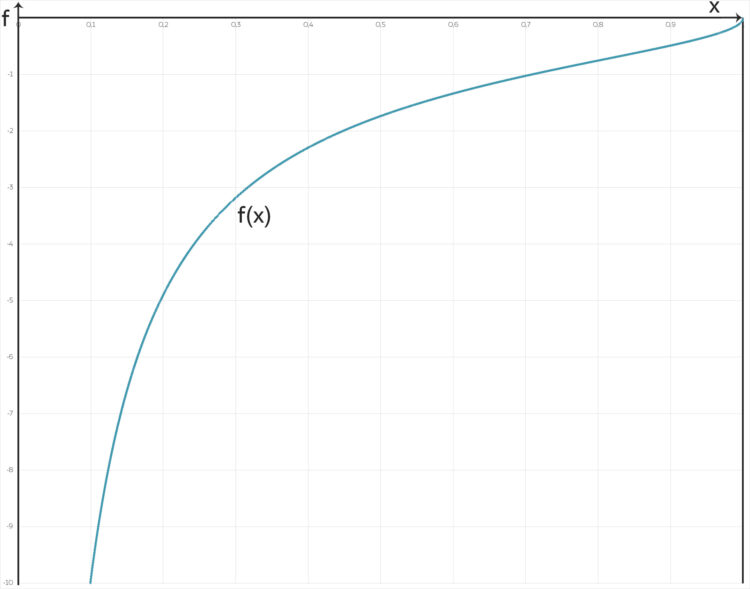
.Jenny Okay, da sieht man, dass die rechte Seite in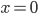 
nicht differenzierbar ist – und in 
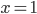ist der Anstieg ja wohl auch 
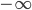. Ja, hmm, dann ist die rechte Seite nicht lipschitzstetig und die Eindeutigkeit der Lösung ist nicht gesichert.
Lila Ja, stimmt. Wir hatten das ja in der Vorlesung und ich hatte zuerst keine Idee, wie ich an weitere Lösungen komme. Dann habe ich my ordinary differential equation of 1st. order in a system of two differential equations 1st. order transformed:
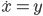
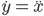
Dazu musste ich die rechte Seite differenzieren und habe bekommen:
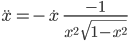
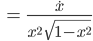
Schließlich habe ich ein System aus 2 Gleichungen erhalten:
Das DGL-System im Phasenraum
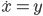
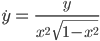
Aus der ursprünglichen Aufgabe geht hervor, dass die rechte Seite für
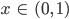
immer negativ ist, also brauche ich das System nur für diese und
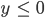
zu betrachten.
Jenny Schön! Die rechte Seite ist noch schwieriger geworden durch das Differenzieren. Außerdem hast du nur einen Anfangswert für 2 Differenzialgleichungen.
Lila Yes! Dann habe ich den Phasenfluss gezeichnet. Zu jedem Punkt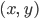 
kann ich 
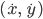berechnen, das ist dann die Richtung, in die sich jeder Punkt bewegt.
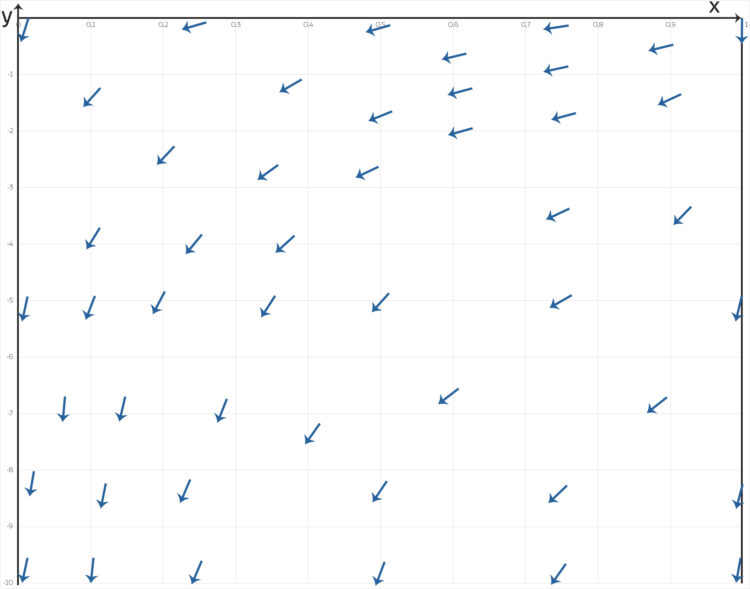
Jenny Lila, du bist so numerisch und so visuell. Hat denn Anna Kratofil das akzeptiert?
Lila Ja, ich glaube schon, sie hat es gewusst, ich habe nämlich versucht, a l l e Aufgaben numerisch zu lösen.
Jenny Aaah, deshalb hast du eine numerisch unlösbare Aufgabe bekommen! Haha.
Die analytische Lösung der AWA
Lila Hmm. Naja, jedenfalls habe ich im Phasenfluss gesehen, dass aus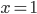 
eine Lösung herausgeht, und die habe ich versucht zu finden. Und – es war gar nicht schwer, du wendest die Methode der Trennung der Veränderlichen an, bringst alles mit auf eine Seite
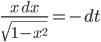
und integrierst dann:
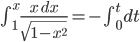
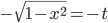
Und das konnte ich auflösen:
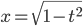
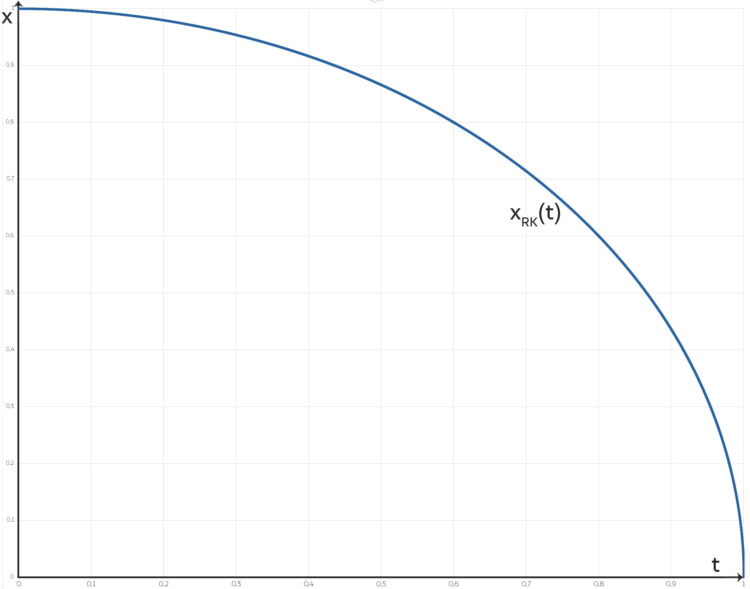
Jenny Okay, gut, dass das so geklappt hat. Und wie sieht die Lösung grafisch aus?
Lila Hier:
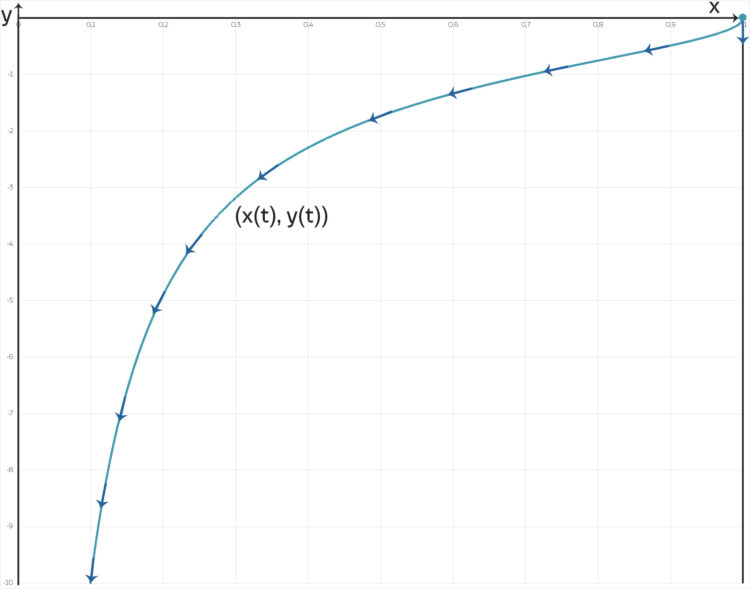
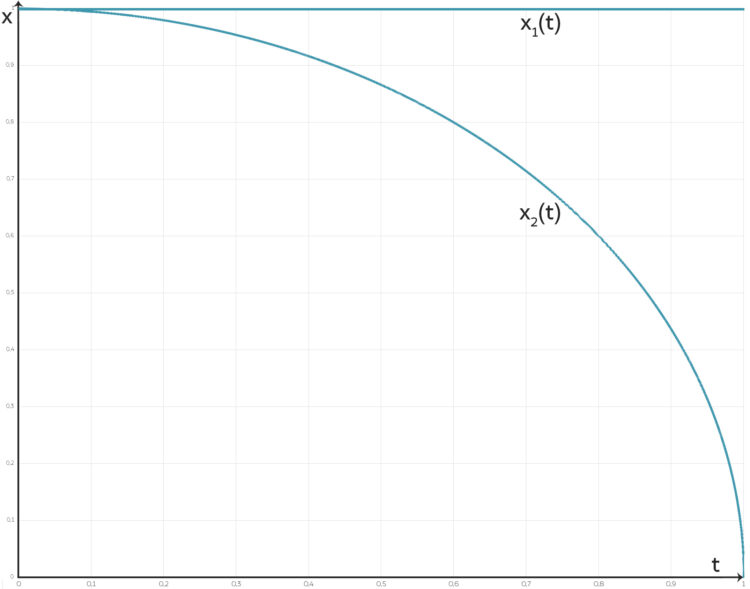
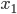und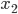 
in Abhängigkeit von der Zeit.
Jenny Okay, dann hast du deine zwei Lösungen. Aber sag mal, gibt es denn nicht noch viel mehr? Die rechte Seite ist ja stetig, dann kann es keine isolierten Lösungen geben. Dann gibt es Lösungsscharen, den Integraltrichter von Kamke…
Lila Richtig, ich habe mir wieder meinen Phasenfluss angeschaut und überlegt, dass die nichttriviale Lösung nicht unbedingt bei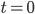 
den Gleichgewichtspunkt 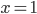verlässt.
Jenny Great!
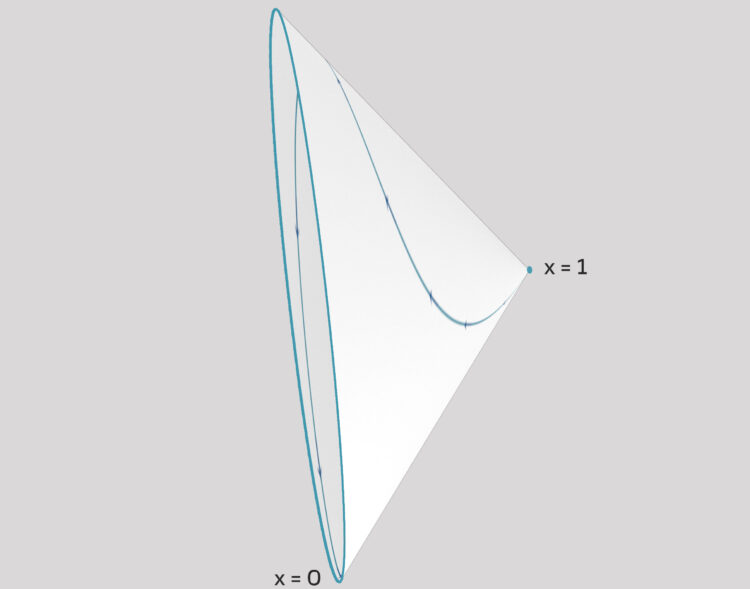
Der Integraltrichter
Lila Okay, also die Lösung könnte ja zuerst im Ruhezustand verweilen und dann später den Ruhezustand verlassen, vielleicht zur Zeit
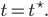
Das packe ich alles in eine Formel:
Ich habe eine ganze Lösungsschar – nur den Namen konnte ich mir nicht merken.
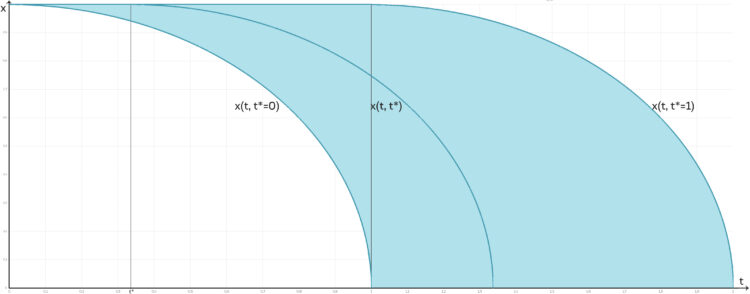
Jenny Ja, genau, das ist der Integraltrichter!
Lila Das hat Krotofil auch gesagt.
Jenny Dein Anfangswert
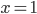
ist ja für das System unterbestimmt. Alle 
-Werte sind zugelassen. Wenn du im Phasenraum diese Kante zu einem Punkt zusammenziehst, erhälst du einen Trichter, einen Funnel, auf dem dann die Lösungen liegen.
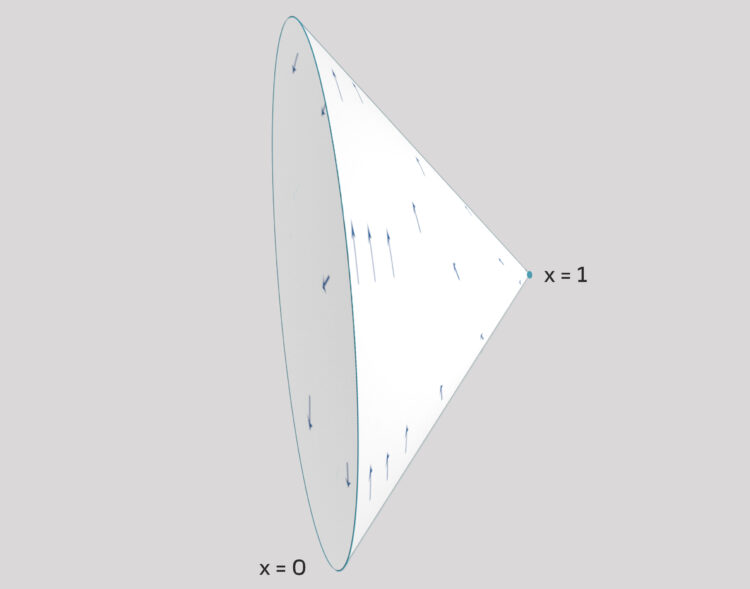
Wenn du im Zeitbereich bist und vielleicht noch mehr Dimensionen hast, dann bilden die Lösungen, die vom Anfangswert ausgehen, auch einen Trichter, einen Funnel, verstehst du, Lila?
Lila Okay, das wäre ja bei mir a very curved funnel?
Jenny Haha, yes.
***
Übungsaufgaben
- Überprüfe, ob die parameterabhängige Lösung die AWA löst.
- Gibt es nicht doch die Möglichkeit, nichttriviale Lösungen numerisch zu berechnen?
- Wie sieht die Lösungsschar auf Jennys Integraltrichter aus?
Lösungen
- Ja, das stimmt.
- Ja, wenn man anstelle des Anfangswertes (und gleichzeitig der Gleichgewichtslösung)
besser
wählt, erhält man mit dem Runge-Kutta-Verfahren die nichttriviale Lösung.
