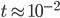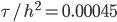Rike fährt zu ihrer Schwester Jule nach Aachen. Die hat ihr Informatikstudium erfolgreich abgeschlossen, hat sich für ein Masterstudium an der RWTH Aachen entschieden und ist nun schon das 1. Jahr dabei. Rike muss einfach mal raus aus Berlin. Sie ist schon lange zusammen mit Ben im Home Office. Sie testet verschiedene Software zur intelligenten und selbstlernenden Mustererkennung für eine spezielle Anwendung. Doch der Auftraggeber hat den Auftrag zurückgezogen und Rike wurde gekündigt. Sie ist ziemlich wütend darüber.
Jule Hi, Rike! Schön, dass du da bist! Wie geht es dir?
Rike Hi, Jule! Ach ja, du weißt es ja schon, ich habe meinen Job verloren.
Jule Hmm. Suchst du schon was Neues?
Rike Ja, ich überlege erstmal, was ich will. Zuerst habe ich mich ausgeruht, bin spazieren gegangen, habe Musik gehört, Youtube geschaut und habe viel nachgedacht.
Jule Schön! Worüber hast du nachgedacht?
Rike Über die Asymmetrie der Zeit.
Jule Okay, spannendes Thema!
Rike Ja, allerdings. Kennst du Wheelers Arbeit Frontiers of Time, sein Urnen-Modell, oder Tenet?
Jule Ja, Tenet habe ich gesehen, aber Frontiers of Time kenne ich nicht.
Rike Das ist sozusagen die wissenschaftliche Grundlage zur Untersuchung, ob Zeit eine sinnvolle physikalische Größe ist und ob sie umkehrbar ist. Wheeler meint, sie spielt nur im menschlichen Denken eine zentrale Rolle, in der Physik oder Natur nicht. Vor allem steht die Zeit für den deterministischen Ablauf von Vorgängen.
Jule Aha! Damit beschäftige ich mich jeden Tag. Ich würde das nicht in Frage stellen.
Die Wärmeleitungsgleichung
Rike Doch! Das musst du! Schau mal, wenn wir zum Beispiel die Wärmeleitungsgleichung nehmen:
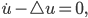
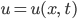 ... beschreibt die Temperatur in einem Objekt. Die Gleichung ist skaliert, die Temperaturverteilung
... beschreibt die Temperatur in einem Objekt. Die Gleichung ist skaliert, die Temperaturverteilung 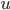 ist bis auf eine additive Konstante eindeutig bestimmt und meine Konstante ist Null.
ist bis auf eine additive Konstante eindeutig bestimmt und meine Konstante ist Null.
Jule ???
Rike Die Gleichung beschreibt, wie sich die Temperaturverteilung eines Objektes mit der Zeit ändert. Wenn du ein Objekt mit sehr unterschiedlichen Temperaturen hast, dann wird im nächsten Zeitschritt ein Ausgleich der Temperaturen stattfinden: nämlich da, wo die größten Differenzen sind.
An diesen Stellen wandern die „heißen“ Teilchen in das „kalte“ Gebiet. Die heißen Anteile werden weniger, die kalten, vor allem an der Grenze zum Warmen, werden wärmer. Vom Gradienten werden nochmals die Differenzen gebildet, eben die 2. räumliche Ableitung. Kurz: Die zeitliche Änderung der Temperatur wird durch die Diffusion beschrieben, das ist das Gesetz, verstehst du?
Jule Na gut, das leuchtet mir ein.
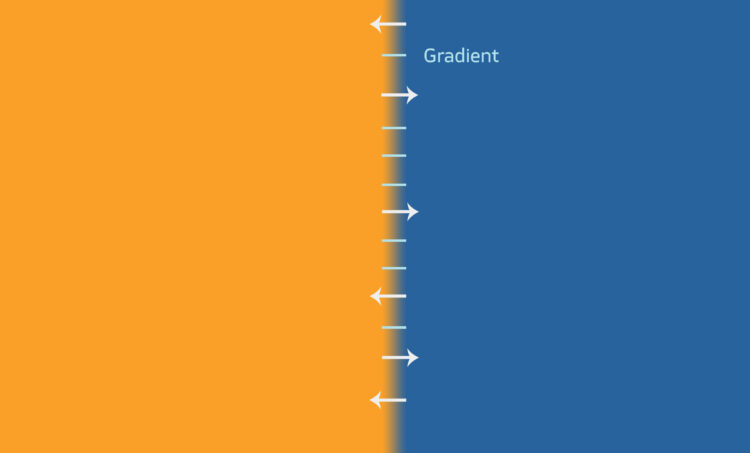
Rike Schön, dann nehmen wir mal nur eine Raumdimension:
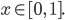
Am Rand des Gebietes fordern wir die allereinfachsten Bedingungen:
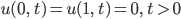
Jule Hey, dann ist es am Rand ja ziemlich kalt!
Rike Ja, das bedeutet, dass das Objekt am Rand konstante Temperatur hat, eben die kälteste. Das Objekt wird am Rand gekühlt.
Jule Okay, hmm, dann wird jede Lösung nach Null gehen, stimmt’s?
Rike Ja, stimmt, Jule. Ich habe eine Dreiecks-Anfangsverteilung genommen, ich wollte unbedingt mit einer nicht differenzierbaren Funktion starten.
Diskretisierung der Wärmeleitungsgleichung
Dann habe ich die DGL. diskretisiert: Im Intervall 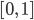 habe ich die Punkte
habe ich die Punkte

betrachtet, mit gleichem Abstand 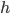 :
:
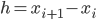 .
.
Die Zeitachse habe ich ebenfalls in gleichlange Teile geteilt:

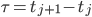 .
.
Jule Schön!
Rike Für die 1. Zeitableitung nehme ich die Änderung der Temperaturverteilung bezogen auf eine kleine Zeiteinheit 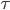 :
:
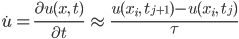
Für die 2. Ortsableitung nehme ich eine geschickte Differenz des Gradienten der Temperaturverteilung:
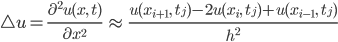
Jule Hmm, das überschaue ich jetzt nicht…
Rike Das passt schon. Die Randbedingungen ergeben die Gleichungen:
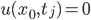
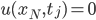
für alle Zeiten 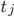 .
.
Jule Klar.
Das explizite Differenzenschema
Rike Wenn wir die Diskretisierung in die Wärmeleitungsgleichung einsetzen, können wir das nach der Funktion 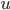 zum nächsten Zeitschritt umstellen und erhalten einen direkten Algorithmus, das explizite Differenzenschema:
zum nächsten Zeitschritt umstellen und erhalten einen direkten Algorithmus, das explizite Differenzenschema:
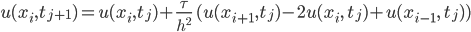
Jule Hört sich überschaubar an. Konvergiert das zur Lösung?
Rike Ja, wir haben die Konvergenz im quadratischen Mittel und für die Stabilität müssen nur die sogenannte Crank-Nicolson-Bedingung erfüllen
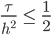 .
.
Jule Okay, dann musst du die Zeitschritt eben recht klein wählen.
Rike Ja, das habe ich gemacht, und es hat gut geklappt. Schau mal, wenn ich mit der Dreiecksfunktion starte, ist die Spitze nach sehr kurzer Zeit abgeflacht.
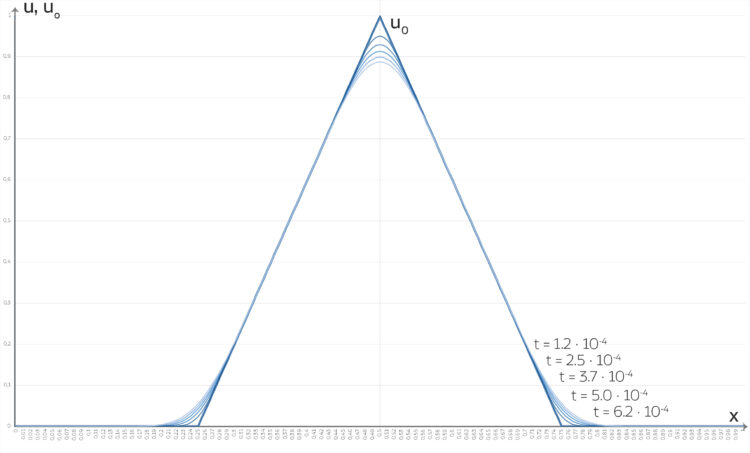
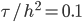 für Zeiten
für Zeiten  . Der Startpunkt ist eine Dreiecksfunktion
. Der Startpunkt ist eine Dreiecksfunktion  , hier in Dunkelblau.
, hier in Dunkelblau.Jule Rike, sehr schön!
Rike Danke. Ich habe mich auch gefreut, dass das so gut geklappt hat.
Jule Konntest du auch das Langzeitverhalten berechnen?
Rike Ja, ich bin mit meinem PC 10² Größenordnungen weitergekommen.
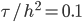 für Zeiten
für Zeiten 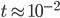
Jule Gefällt mir. Sollen wir das mal an der Uni zu Ende rechnen?
Rike Klar, kannst du machen.
Jule Was ist denn dein Problem?
Die rückwärtige Wärmeleitungsgleichung
Rike Ich wollte prüfen, ob ich aus den Lösungen, die ich zu irgendeiner Zeit 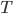 erhalte, die Anfangsbedingungen rekonstruieren kann. Die rückwärtige Wärmeleitungsgleichung eben.
erhalte, die Anfangsbedingungen rekonstruieren kann. Die rückwärtige Wärmeleitungsgleichung eben.
Jule Hört sich ganz wie Tenet an. Ob die Dinge ein Gedächtnis haben? Oder ob man bei einem Zustand entscheiden kann, in welche Richtung er sich entwickelt, hmm, Rike. Wenn du das ausrechnen kannst, dann hast du den Hauptgewinn gezogen!
Rike Haha!
Jule Deine Differenzengleichung geht eben nach vorne. Die Diffusion sollte rückwärts stattfinden? Wie hast du es gemacht?
Rike Du hast es schon gesehen. Wir starten bei einer Zeit

und führen eine neue Zeit
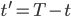
ein. Die neue Zeit 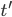 läuft dann „vorwärts“ von 0 bis T, wenn die normale Zeit
läuft dann „vorwärts“ von 0 bis T, wenn die normale Zeit 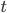 rückwärts von T nach 0 läuft. Ich diskretisiere das neue Zeitintervall:
rückwärts von T nach 0 läuft. Ich diskretisiere das neue Zeitintervall:

Aus der 1. Zeitableitung wird dann:
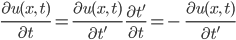 .
.
Damit wird aus der Wärmeleitungsgleichung
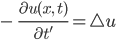
oder
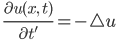
Jule Klar!
Der Rückwärtsalgorithmus
Rike Gut, aus meinem explizitem Differenzenschema wird dann
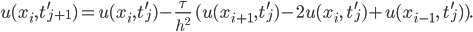
Die Randbedingungen bleiben:
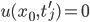
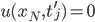
für alle Zeiten 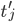 .
.
Jule Okay.
Im Mikrokosmos
Rike Das habe ich numerisch gelöst. Zuerst ist alles schiefgegangen, ich musste den Faktor 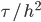 sehr klein wählen und viele Zeitschritte machen, viel mehr als bei der Vorwärtsaufgabe.
sehr klein wählen und viele Zeitschritte machen, viel mehr als bei der Vorwärtsaufgabe.
Jule Aha, der Mikrokosmos in der Zeit. Haha. Welche Größenordnung denn?
Rike 10-2.
Jule Okay. Und dann hast du das Dreieck rekonstruiert?
Rike Ja, hier!
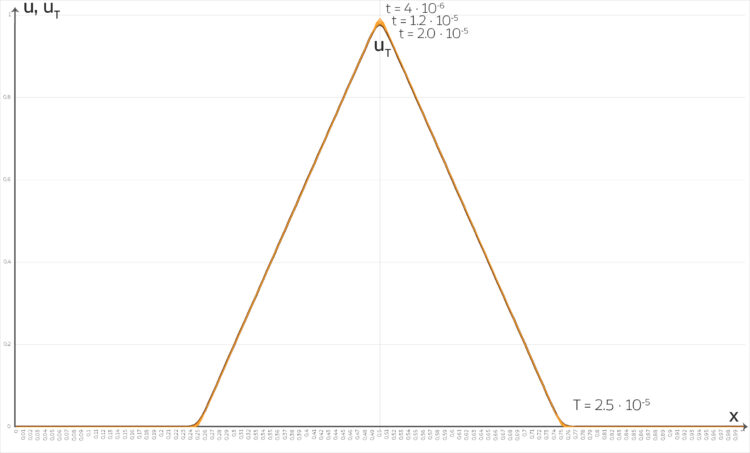
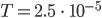 beginnend und
beginnend und 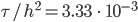 . Der Startpunkt ist
. Der Startpunkt ist 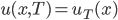 , hier in Braun.
, hier in Braun.Jule Großartig! Du bist super! Meine Schwester!
Im Makrokosmos
Rike Dann habe ich eine Langzeitlösung als Startpunkt genommen, den Faktor 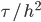 noch mal verkleinert. Aber das war numerisch instabil. Ich habe sehr merkwürdige Lösungen bekommen, sie sehen aus wie Mikroschwingungen, sehr komisch!
noch mal verkleinert. Aber das war numerisch instabil. Ich habe sehr merkwürdige Lösungen bekommen, sie sehen aus wie Mikroschwingungen, sehr komisch!
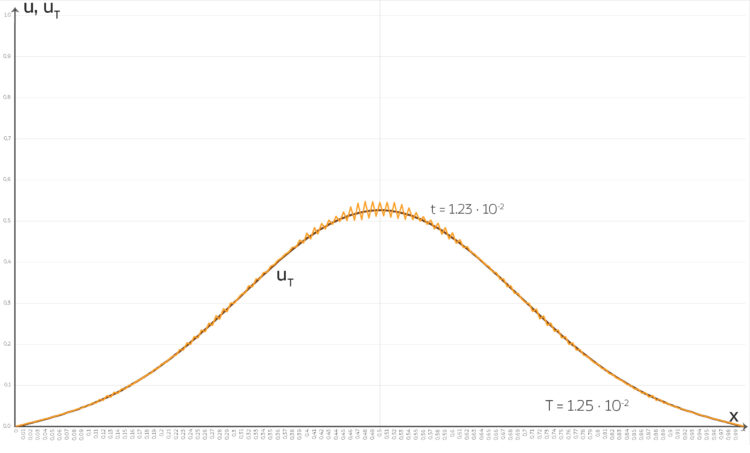
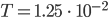 beginnend und
beginnend und 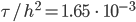
Jule Hmm.
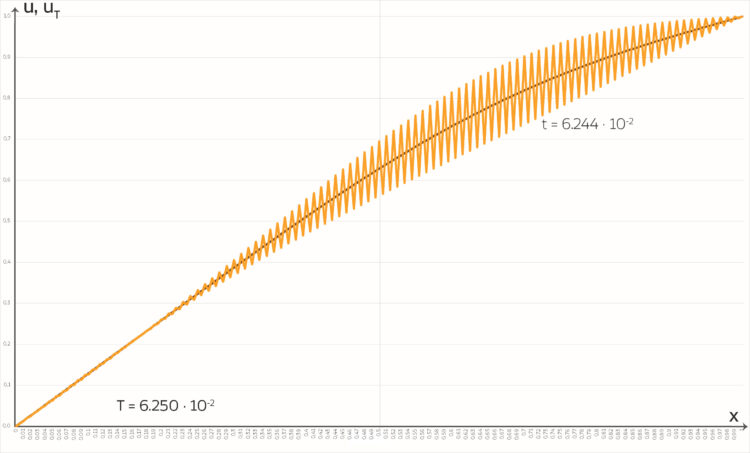
Rike Ich habe erst gemeint, das ist mein Fehler, dann habe ich mit einer anderen Langzeitlösung der Wärmeleitungsgleichung angefangen, eine, wo sich die Temperaturen schon gut verteilt hatten und kein Dreieck mehr zu erkennen war. Aber ich habe nur Blödsinn herausbekommen!
Jule Zeig mal!
Rike Hier! Hier habe ich den Zeitpunkt gezeichnet, wo Oszillationen entstehen, das wird dann immer schlimmer.
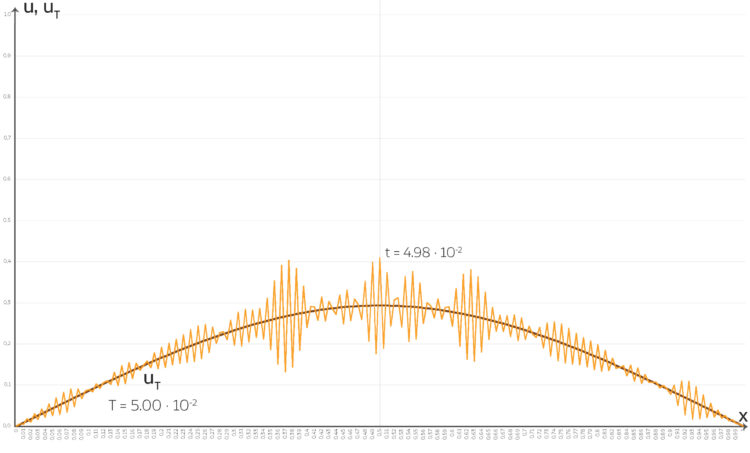
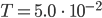 beginnend und
beginnend und 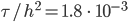 .
.
Fazit
Jule Krass! Hat denn Wheeler eine Erklärung dafür?
Rike Wheeler stellt Anfangswertaufgaben an sich in Frage. Er sagt, die Anfangsbedingungen sind willkürlich gewählt, sie sind sehr unwahrscheinlich und fern vom Gleichgewicht. Das System strebt immer zum Gleichgewicht hin.
Jule Richtig. Das ist bei dir die konstante, triviale Lösung. Aus der kommst du mit deinem Differenzenschema nicht mehr heraus.
Rike Stimmt. Ich komme aus der Null, aus dem Nichts nicht mehr heraus. Jule, das ganze Modell ist falsch, wir sollten die Wärmeleitung als stochastisches System verstehen, die verschiedenen Zustände mit Wahrscheinlichkeiten beschreiben und nicht am zeitlichen Verlauf in die eine oder andere Richtung festhalten.
Jule Hmm. Alles umsonst? Das falsche Modell? Kannst du damit nicht die Wärmeleitung an Außenwänden von Häusern berechnen und – sogar einen Beitrag zum Klimaschutz leisten? Ich meine, die Wärmeleitung wird doch technisch immerzu angewendet?
Rike Ach, Jule, da werden noch viel einfachere Modelle benutzt. Vielleicht kommt der Tag und ich kann etwas Nützliches berechnen, bis dahin haben wir ein großes Nichts, keine Zeit, keine Richtung, wir haben Interaktion, Statistik, Substanz ... Wir sind selbst Teil der Versuche, wir müssen alles testen und messen, doch ich kann nicht mehr.
Jule Gibst du auf?
Rike Ja, ich will nichts mehr ausrechnen.
Jule Nein!
Rike Doch.
Jule Ach, Rike.
***
Übungsaufgaben
- Teste das Langzeitverhalten der Lösungen der Wärmeleitungsgleichung mit demselben Anfangswert wie Rike!
- Wohin streben die Lösungen für andere Randbedingungen, zum Beispiel nichthomogene Dirichletsche:
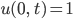
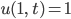
oder
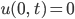
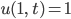
für alle Zeiten
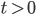 ?
? - Kommt man aus diesen Lösungen mit dem rückwärtigen expliziten Differenzenschema wieder heraus?
Lösungen
- Für die erste konstante nichthomogene Randbedingung erhält man die gleiche Lösung wie im Beitrag, nur die additive Konstante ist 1. Für die 2. Randbedingung streben die Lösungen für ein Langzeitverhalten der Geraden

zu.
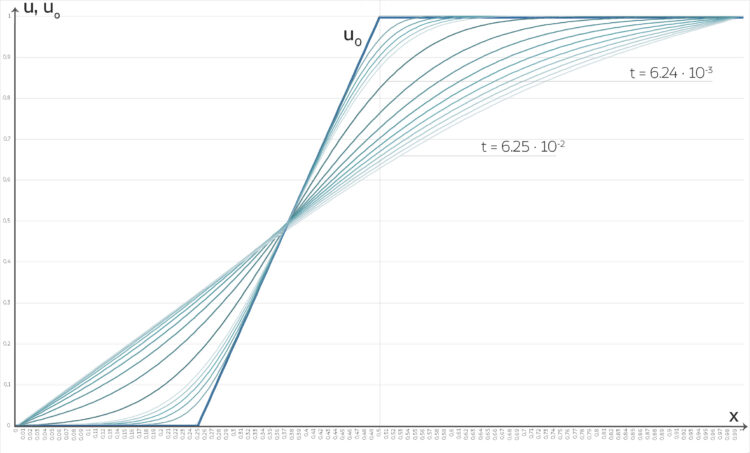
Numerische Lösungen der Differenzengleichungen für die Wärmeleitungsgleichung mit inhomogenen RB und 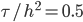 für Zeiten
für Zeiten