Charly besucht Max und Lila in Berlin. Charly fällt gleich auf, dass Lila sehr traurig wirkt.
Charly Hey, Lila, was ist los mit dir?
Lila Hi, Charly, schön, dass du gekommen bist. You know, my grandparents died because of Corona. Jetzt ist auch noch mein Vater erkrankt, immerzu rufe ich zu Hause in Kalkutta an, aber nichts wird besser. Ich muss nach Hause.
Charly I’m so sorry, Lila. Kannst du nicht hierbleiben, ist das nicht besser?
Lila Ich mache mir große Sorgen. Eine Beerdigungsfeier gab es für meine Großeltern leider nicht. Deshalb bin ich hiergeblieben.
Max Lila ist sogar schon geimpft!
Charly Das ist gut! Und dein Studium?
Lila Jetzt im Sommersemester hören wir wieder bei Kubicki Analysis-Vorlesungen, bei Kubicki!
Charly Hmm.
Kubickis klassische PDE-Vorlesung
Lila Ja! Partial Differential Equations, PDEs. Er erörtert, welche PDEs es gibt: Laplace-Gleichung, Wärmeleitungsgleichung, Wellengleichung und erklärt uns Anfangs- und Randbedingungen. Er löst ein paar PDEs und holt ganz weit aus für seine Existenz- und Eindeutigkeitssätze. Ich habe keine Lust dazu. Mir ist das alles zu umständlich. In manchen Fällen gibt es eine Lösung, doch Kubicki beweist nur, dass es eine gibt – genau eine! Zuerst kommen die Existenz- und Eindeutigkeitssätze und dann die Berechnung, hat er gesagt. Wir müssen zuerst das Brouwer Fixed-Point Theorem verstehen, bevor er uns ins nächste Semester lässt.
Charly Ooh! In der Schule machen wir das anders. Das ist ja didaktisch ganz unklug.
Lila Irgendwie kommt der Spaß zu kurz. Als ob man ein dickes Buch nur für den Prof liest, ganz systematisch von vorn nach hinten. Habt Ihr das eigentlich auch so gemacht?
Max Nö, wir haben viel ausgerechnet und viele Projekte gemacht.
Lila Kubicki hängt so an den klassischen Theorien. Dabei gibt es da ganz neue Entwicklungen. Ich habe davon gehört, dass eine Maschine lernt, PDEs numerisch zu lösen, sogar nichtlineare und welche mit Parametern.
Carly Und wie geht das?
Lila Stell dir mal ein Gefäß vor, durch das eine Flüssigkeit fließen soll. Am besten färbt man die mit Mikropartikeln ein, um das Geschwindigkeitsfeld 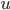 zu beobachten. Links ist eine Quelle, rechts ist das Gefäß offen.
zu beobachten. Links ist eine Quelle, rechts ist das Gefäß offen.
Charly Ach, ja, Navier-Stokes-Gleichungen! Unter dem fängst du wohl nicht an? Lila!
Triviale Lösung
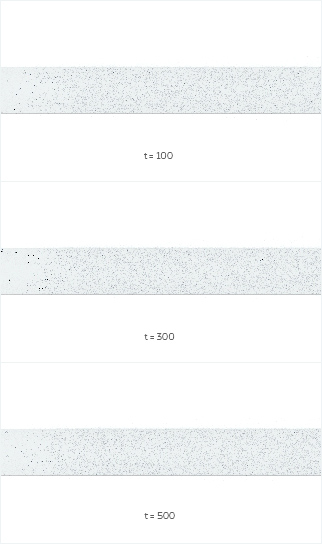
Lila Haha, zur Zeit 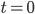 ist das Rohr leer,
ist das Rohr leer,
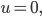
und wir schalten die Quelle ein. Die produziert gleichmäßig die Flüssigkeit und die fließt dann nach kurzer Zeit gleichmäßig durch:
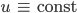
Das ist die triviale Lösung.
Charly Okay.
Nichttriviale Lösungen
Lila Wenn das Gebiet jetzt komplizierter wird, zum Beispiel mit einem Object Of Collision – wie heißt das deutsch?
Charly Kollisionsobjekt.
Lila Klar, Kollisionsobjekt, ein zusammen – ge – setztes Substantiv! So deutsch!
Charly Ist schon okay.
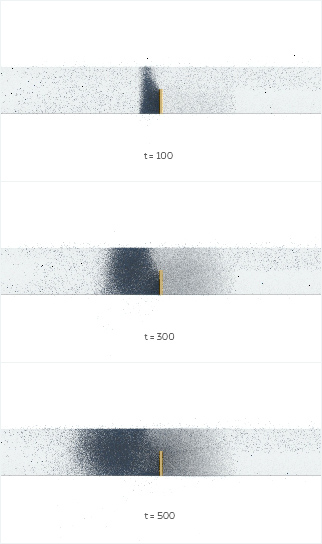
Lila Wenn also an einem Kollisionsobjekt ein Teil der Flüssigkeit abprallt und dabei die Geschwindigkeit abnimmt, dann haben wir schon 2 Parameter und ein ganz anderes Lösungsverhalten. Schaut mal hier:

Charly Okay. Die Flüssigkeit fließt weiter (zeitlich) gleichmäßig durch, aber nicht örtlich gleichmäßig, jetzt nur in der oberen Hälfte.
Lila Ja. Wenn jetzt noch weniger Teile abprallen und deren Geschwindigkeit noch langsamer wird, dann verstopft früher oder später die Röhre. Der Durchfluss wird immer geringer.
Charly Okay, klar.
Lila Da siehst du, dass wir 2 verschiedene Lösungsszenarien haben: Durchfluss und Verstopfung. Bei realen Flüssigkeiten kann es noch zu Turbulenzen kommen.
Charly Stimmt. Kann ich mir vorstellen. Lila, ist es denn nicht auch wichtig, wann die Röhre verstopft?
Lila Ja richtig, ob sie verstopft und wann.
Charly Das kann lebensrettend sein.
Fourier Neural Operator-Methode für PDEs
Lila Stimmt, deshalb will ich unbedingt die Lösungen berechnen. Diese neue Methode, die Fourier Neural Operator Method for PDEs besteht aus einem Teil für Maschinelles Lernen und einem Fourier Transformation Part. Aus den Ausgangswerten, dem Gebiet, den Anfangs- und Randbedingungen, dem Kollisionsobjekt und seinen Eigenschaften lernt die Maschine anhand von einigen Beispielen das Lösungsverhalten. Mit Bilderkennung usw.
Charly Bilderkennung haben wir eben auch gemacht.
Lila Haha. Man testet Minilösungen in ganz kleinen Gebieten und versucht, die Abhängigkeit der Lösung in einen Integraloperator zu packen. Das testet man dann wieder und prüft die Abweichung im quadratischen Mittel im Allgemeinen. Mit diesem Integraloperator faltet man dann die Anfangsbedingungen.
Charly Falten?
Lila Ja, man integriert die Anfangsbedingungen mit einem Gewicht, Convolution heißt das.
Charly Okay. Da steckt aber doch viel Knowhow drin. Da hast du ja doch was bei Kubicki gelernt.
Lila Na! Aber nicht Maschinelles Lernen. Ich musste selbst da durch und versuchen, aus 320 x 180-Pixel-Bildern die Lösungen zu klassifizieren. Die Erfinder der Methode haben da am Caltech sogar nur 64 x 64 Pixel-Bilder benutzt.
Charly Das hast du gemacht?
Lila Yes.
Max Ja, das hat sie. Sie hat ewig drangesessen.
Charly Ooh, Mann! Also du hast mit einer Software Bilder klassifiziert und die Parameter für die Integration gefunden.
Lila Yes.
Charly Aber fehlen da nicht viel zu viele Informationen, um wirklich eine Vorhersage zu treffen. So ein 64 x 64 -Pixel-Bild kann doch nicht viel leisten? Du würdest mich kaum auf so einem Bild erkennen.
Vergleich von „kleinen“ und „großen“ Lösungen
Max Wartet mal! Hier ist Charly auf 64x64 Pixeln!

Lila Haha, klar erkenne ich dich. 64 x 64 Pixel sind eine Menge Information.
Charly Na gut.
Lila Bei den PDEs hängt die Lösung oft sehr sensibel vom Gebiet, der Auflösung und den Parametern ab, manchmal verzweigt sich die Lösung sogar. Doch aus den kleinen Bildern kann man das qualitative Lösungsverhalten erkennen. Jetzt braucht man nur noch eine Methode, um die kleinen Bilder intelligent groß zu rechen.
Max Also, wenn ich so Minibilder von Kunden kriege und die dann groß rechne, sehen die immer so schwammig aus, die Kanten werden unscharf, minimale Unregelmäßigkeiten werden dann zu großen Flecken, es ist ein großer Mist! Eigentlich geht es kaum, weil ja die Informationen von so vielen Pixeln fehlt. Das normale Großrechnen interpoliert ja auch nur.

Lila Stimmt, minimales Rauschen wird groß gerechnet. Genau das muss man verhindern. So sind die Autoren, wo übrigens auch ein Inder dabei ist, darauf gekommen, die Lösungen in ihre Schwingungen zu zerlegen. Die Schwingungen mit geringem Einfluss werden danach aussortiert.
Charly Ach, das ist das Rauschen, das können die aussortieren!?
Lila Yes!
Max Wenn du das auch hinkriegst, kannst du alle Bilder ohne Rauschen hochrechnen. Das wäre super!
Lila Hier zeige ich euch mal den Vergleich von „kleinen“ und „großen“ Lösungen:


Charly Hey, Lila, das ist super! Du bist so cool! Es wäre so schade, wenn du dein Studium nicht beendest. Danach könntest du direkt beim Caltech anfangen!
Max Du musst weitermachen, Lila, hier bei uns in Berlin! Lass uns zusammenbleiben!
Lila Es dauert so lange, bis ich meinen Abschluss habe. Ich weiß nicht.
