Max hat Liebeskummer, denn Lila ist tatsächlich nach Indien zurückgekehrt. Ihr Vater ist an Corona gestorben. Außerdem ist sie von ihrem Mathestudium enttäuscht. Max hat den geplanten Urlaub dennoch genommen und ist in Berlin geblieben. Er versteht die Welt nicht mehr. Bloß gut, dass Charly zu ihm nach Berlin kommt. Auch ihm tut es leid, dass Lila Max verlassen hat. Max und Charly laufen durch Berlin, sie suchen (und finden) die beste Party. Als sie dann irgendwann am nächsten Morgen in Max‘ Küche stehen und Kaffee kochen wollen, fällt Charly die Düsseldorfer Kaffee-Aufgabe ein.
Charly Morgen, Max, wie geht’s?
Max Morgen, Charly, aaaaaach …
Charly Du hast aber eine tolle Kaffeemaschine, ich mache uns mal einen Kaffee. Das hilft. Kennst du schon die Düsseldorfer Kaffee-Aufgabe?
Max Nö!
Die Düsseldorfer Aufgabe
Charly Warte mal, ich suche sie raus! … Hier! Es ist eine Aufgabe über parameterabhängige Exponentialfunktionen. Sie dient der Vorbereitung aufs Abi. Die Schüler sollen die Abkühlung eines Bechers Kaffee bei einer Raumtemperatur von 18 °C durch eine Exponentialfunktion modellieren. Es gibt 2 Messergebnisse:
| Zeit t [min] | Temperatur T [°C] |
| 1 | 71 |
| 10 | 51 |
und den Ansatz
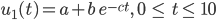
mit reellen Parametern
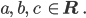
Max Okay. 3 Parameter und 2 Messergebnisse?
Charly Na, die 18 °C eben noch.
Max Na gut. Dann setze ich das eben ein.
Charly Richtig. Die 18 °C werden natürlich erst nach sehr langer Zeit erreicht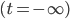 
. Dann kriegt man
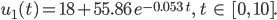
Max Okay, hört sich nicht so spannend an. Wo ist das Problem?
Charly Warte, es geht noch weiter. Nach 10 min soll „kalte Milch zugeführt“ werden und gleich nach 11 min erneut gemessen werden. Dann erhält man mit demselben Ansatz die Lösung
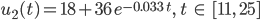
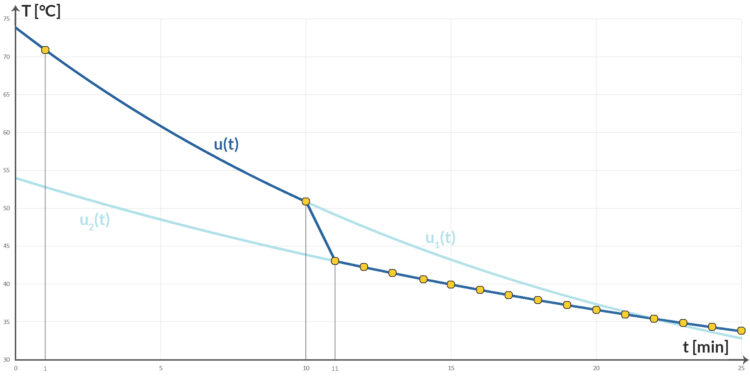
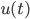(dunkelblau) der Düsseldorfer Kaffee-AufgabeKritik
Eine Schülerin hat das zu Hause nachgemessen und die Werte bezweifelt. Dann habe ich den Physiklehrer unserer Schule gefragt, was er dazu meint, der hat nur gelacht.
Max Die Messwerte liegen alle auf einer Kurve? Sollen wir das mal messen? Warte, ich hole ein Thermometer.
Charly Ja, das machen wir. Hast du noch Becher?
Der Versuchsaufbau von Max und Charly
Max Klar, ich habe 3 verschiedene Becher. Wir füllen alle mit einer Doppeltasse aus meiner Maschine und messen dann.
Charly Gut, ich schreibe das Protokoll!
Max Hey, Charly, die Temperatur ist nicht konstant innerhalb des Bechers, sie schwankt sehr stark, je nachdem wo ich messe.
Charly Dann nimm doch immer den gleichen Punkt – am besten den Mittelpunkt.
Max Klar! Mache ich. Das Temperatur kann ich aber nur am Mittelpunkt der Oberfläche messen, ich habe kein Innenthermometer.
Charly Ja, ich weiß.
…
Ihre Messergebnisse
Max Charly, die Temperatur fällt nicht exponentiell! Manchmal fällt sie gar nicht! Sogar nach der Zugabe von Milch! Wie kann das sein?
| t [min] | T [°C] 1. Becher | T [°C] 2. Becher | T [°C] 3. Becher |
| 0 | 55.6 | 61.6 | 59.1 |
| 1 | 52.5 | 56.1 | 56.2 |
| 2 | 50.8 | 56.0 | 55.2 |
| 3 | 49.3 | 54.8 | 53.6 |
| 4 | 48.8 | 53.6 | 51.8 |
| 5 | 46.0 | 51.7 | 51.6 |
| 6 | 46.6 | 49.4 | 51.3 |
| 7 | 41.7 | 49.8 | 48.2 |
| 8 | 44.2 | 46.6 | 47.5 |
| 9 | 46.3 | 48.4 | 46.0 |
| 10 | 39.8 | 46.6 | 49.2 |
| 11 | 41.6 | 46.7 | 47.8 |
| 12 | 37.6 | 43.5 | 44.4 |
| 13 | 38.2 | 40.4 | 43.6 |
| 14 | 37.3 | 43.0 | 41.2 |
| 15 | 38.3 | 41.0 | 43.1 |
| 16 | 39.0 | 33.7 | 42.4 |
| 17 | 36.5 | 40.3 | 39.3 |
| 18 | 37.6 | 38.7 | 41.5 |
| 19 | 36.5 | 36.6 | 38.5 |
| 20 | 36.0 | 38.7 | 40.1 |
| 21 | 34.0 | 37.0 | 37.2 |
| 22 | 33.8 | 35.5 | 36.0 |
| 23 | 36.1 | 33.7 | 37.2 |
| 24 | 33.2 | 36.3 | 37.0 |
| 25 | 32.5 | 34.5 | 36.4 |
[Diese Werte sind bei einer sich ändernden
Außentemperatur von 17.7 - 18.8 °C
gemessen worden; die Milch hatte 12 °C.]
Probleme des Temperaturmessens
Charly Hey! Max! Du hast ja selbst gesagt, die Temperatur ist nicht konstant im Becher. Da finden Wärmeleitungs- und Konvektionsprozesse statt, ja, und auch noch Wärmestrahlung, sagt unser Physiklehrer. Es wäre besser, die m i t t l e r e Temperatur des Kaffees zu messen.
Max Haha! Das kann ich nicht. Die Messergebnisse sind unmöglich zu reproduzieren. Ist das nicht verrückt, Max?
Charly Ja, es ist verrückt. Schau mal, wie die Messwerte aussehen.
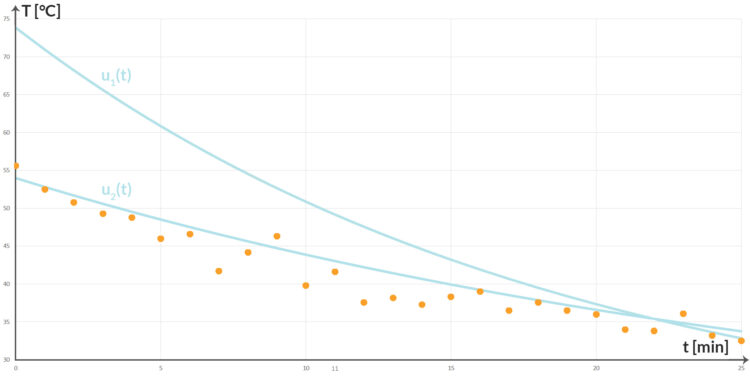
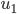und 
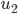der Abi-Aufgabe (hellblau)Max Es geht auf und ab, doch im großen Ganzen sinkt die Temperatur. Eventuell kannst du gar keine E-Kurve durch alle Punkte legen, Charly! Sollen wir nur die beiden Messwerte für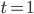 
und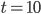 
nehmen? So ist doch die Intention der Aufgabe?
Charly Ich glaube, es ist keine gute Idee, nur 2 von 11 Messwerten zu berücksichtigen. Lass uns mal eine E-Kurve finden für die Zeit bis "zur kalten Milch" und eine danach. Jede Kurve soll halbwegs nahe bei den Messpunkten sein.
Max Okay. Ist das nicht etwas schwierig für Abiturienten? Kommen die auch auf solche Ideen?
Charly Willst du wirklich die Kaffeetemperatur-Kurven an die Mathe-Themen anpassen? Kein Raum für Kreativität oder für Wahrheitssuche? Immer nur mit dem Taschenrechner die Welt verstehen?
Max Ist ja gut, Charly, war nicht so gemeint. Mathe war für mich immer etwas schwierig, erst mit Rike habe ich Vieles besser verstanden. Gut, wir versuchen's mit deinem Vorschlag!
Charlys Ansatz: Die Methode der kleinsten Quadrate
Charly Schön. Wir nehmen denselben Ansatz:
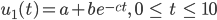
mit den Parametern
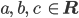
und vergleichbaren Werten
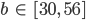
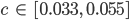
Max Alles klar!
Charly Die Messwerte kriegen die Bezeichnungen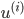 
, also zu jedem Zeitpunkt 
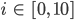haben wir den Messwert 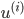. Dann rechnen wir die Differenz der Messwerte von der Funktion 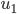zur Zeit 
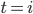aus:
.
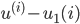Die Differenz müssen wir quadrieren, wir nehmen am besten die Methode der kleinsten Quadrate, so:
.
.
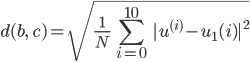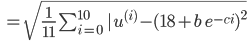Max Was jonglierst du da?
Charly Das ist die berühmte Methode der kleinsten Quadrate. Jeder punktuelle Fehler wird quadriert, damit sich positive und negative Differenzen nicht aufheben, alle diese Fehler, bei uns sind es 11 für die 1. Funktion, werden aufsummiert und durch 11 geteilt, dann haben wir den mittleren Fehler. Zum Schluss noch die Wurzel, damit wir die richtigen Einheiten kriegen und nicht Temperatur zum Quadrat. Übrigens eine Idee von Gauß.
Max Soso! Von Gauß! Na gut.
Charly Diese Differenz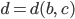 
soll minimal werden:
Max Aha! Eine Funktion mit 2 Parametern!
Grafische Suche des minimalen Fehlers
Charly Lass uns die mal zeichnen. Okay, warte …
Max Ja, die hat ein Minimum. Kannst du das genau herausfinden?
Charlys Lösung
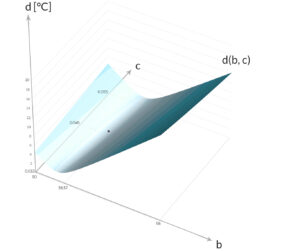
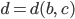als Fläche mit einem Minimum bei 
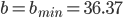und 
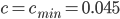bei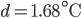 
.Charly Ja, klar, bei
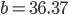
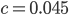
haben wir dann ein Minimum von
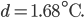
Max Okay. Dann haben wir die Kurve mit der minimalen Abweichung für den gelben Becher, ich versuch‘s mal:
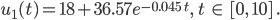
Charly Okay. Das müssen wir noch einmal für die 2. Funktion machen.
Max Richtig.
Charly Warte, …, ja, wir kriegen
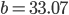
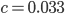
Das Minimum ist hier bei
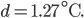
Max … Also dann haben wir die 2. Funktion vollständig bestimmt:
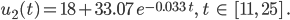
Jetzt können wir die beiden Funktionen zusammensetzen, zeig mal, wie die aussehen!
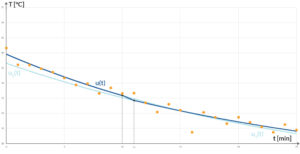
Charly Hier!
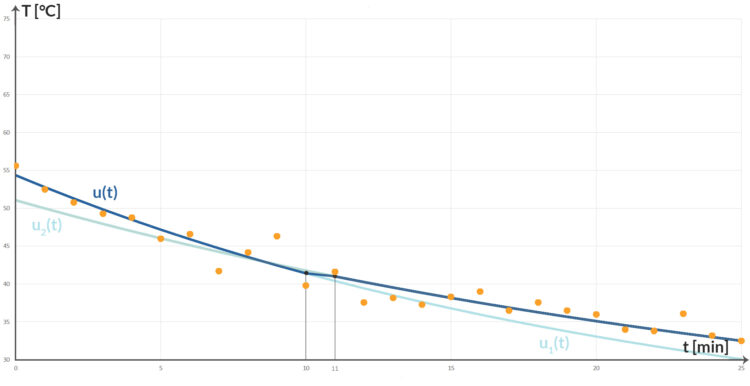
für den 1. Becher mit 2 Exponentialfunktionen, die minimal im quadratischen Mittel von den Messwerten abweichen.Max' Fazit
Max Hmm. Erstens: Anfangs kühlt der Becher den Kaffee auf 56 °C ab, zweitens haben wir nicht reproduzierbare Messwerte, drittens hat die kalte Milch keine Abkühlung gebracht und viertens liegt der mittlere Fehler unserer Messwerte im Vergleich zum Ansatz bei ca. 1.5 °C. Vielleicht ist der 1. Becher nicht so gut geeignet und die Abkühlung muss mit intelligenter Physik modelliert werden? Wärmeleitung, Strahlung, Konvektion usw. – wie dein Physiklehrer meinte. Aber deine Idee mit der Gauß-Methode funktioniert super! Is' echt geil.
Charly Max, haha, you got it!
Übungsaufgaben
- Finde selbst die Lösungen für den 2. und 3. Becher.
- Interpretiere die Ergebnisse.
Lösungen
- Für den Pappbecher erhalten wir mit den Messwerten aus der Tabelle folgende Lösung:
Lösung für den 2. Becher.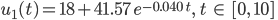 
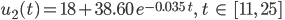
Wir haben dann ein Minimum von
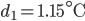
bzw.
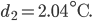
Für den (dickwandigen) Porzellanbecher erhalten wir
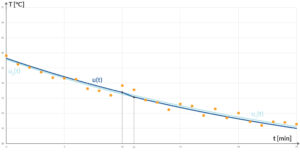
Lösung für den 3. Becher.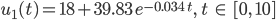 
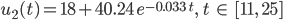
mit den Minima von
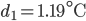
und
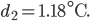
- Der Kunststoffbecher hat den Kaffee anfangs am meisten abgekühlt. Die Hinzugabe von kalter Milch ändert das Abkühlungsverhalten nicht wesentlich. Im 3. Becher kühlt der Kaffee am ehesten nach dem Exponentialgesetz mit negativem Exponenten ab. Der mittlere quadratische Fehler ist hier am geringsten: 1.2 °C.
