Rike hat 2 Schwestern: Jule und Paula. Beide sind sehr Informatik-affin. Paula studiert Games Engineering. Als Schülerin hatte sie Effi Briest mathematisch analysiert – mit Rikes Hilfe. Nun treffen sich beide in München und diskutieren eine spezielle Kurve im Zusammenhang mit dem RSA-Algorithmus.
Paula Hi Rike, wie geht es dir? Schön, dass du gekommen bist.
Rike Hi Paula, schön hast du es hier. Wie geht es dir?
Paula Eigentlich ganz gut. Ich bin gut durch die Corona-Zeit gekommen, durfte die Rechner der TU benutzen. Erinnerst du dich an die Effi-Briest-Geschichte?
Rike Hey! Und ob! Das war toll!
Wörter beim RSA-Algorithmus
Paula Jetzt habe ich wieder mit Wörtern zu tun!
Rike Echt? Krass! Erzähl‘ mal!
Paula Es geht um den RSA-Algorithmus – sagt dir das was?
Rike Haha! Den habe ich mal Max erklärt. Aber was hat das mit Wörtern zu tun? Wir haben nur Zahlen chiffriert.
Paula Siehst du! Also, bei uns in München geht das so: Wir wollen Wörter chiffrieren. Die bestehen aus Buchstaben aus einem endlichen Alphabet.
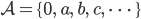
mit der Länge  . Die Null brauchen wir, um Wörter in einheitlich lange Blöcke zu packen. Wenn du das Wort
. Die Null brauchen wir, um Wörter in einheitlich lange Blöcke zu packen. Wenn du das Wort

hast, ist es dasselbe wie
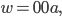
aber nicht dasselbe wie
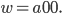
Rike Klar, verstehe, 1 ist ja auch nicht dasselbe wie 100. Aber ihr rechnet doch nicht wirklich mit Zeichenketten?
Paula Haha, nein, wir vergleichen keine Zeichenketten und rechnen nicht mit Zeichenketten. Wir wandeln die Wörter ganz schnell in Zahlen um.
Rike Aha! Und wie?
Paula Zuerst erklären wir eine isomorphe Abbildung  von
von 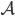 in die Restklasse
in die Restklasse 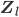 :
:

Dh., wir ordnen jedem Buchstaben eine Zahl von 0 bis  zu, so:
zu, so:
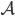 | 0 |  | 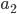 |  | 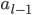 |
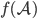 | 0 |  | 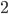 |  |  |
Abbildung von Buchstaben/Zeichen aus dem Alphabet auf Zahlen in 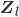
Wörter im l-Stellenwertsystem
Bei Wörtern machen wir das buchstabenweise: Aus

wird
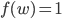
und aus
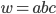
wird
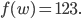
Allgemein wird aus
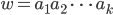
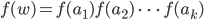
Diesen Koeffizienten 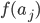 gebe ich gleich mal eine Bezeichnung:
gebe ich gleich mal eine Bezeichnung:
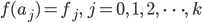
Rike Okay, und dann?
Paula Diese Wörter 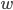 , die jetzt Zahlen
, die jetzt Zahlen 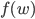 sind, verstehen wir als Zahlen im Stellenwertsystem zur Basis
sind, verstehen wir als Zahlen im Stellenwertsystem zur Basis  . Von denen berechnen wir den Wert
. Von denen berechnen wir den Wert 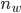 in der Dezimaldarstellung:
in der Dezimaldarstellung:
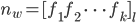
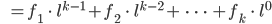
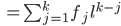
Rike Hmm, nicht schlecht. Aber was ist, wenn ihr mehr als 10 Buchstaben in eurem Alphabet habt? Dann sind die Koeffizienten 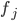 doch zweistellig?
doch zweistellig?
Paula Ach ja, das haben wir uns beim Hexadezimalsystem abgeguckt:
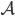 | 0 | 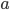 | 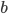 |  | 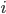 | 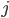 |  |  |  |  | 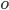 |
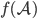 | 0 |  | 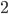 |  | 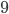 | 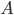 | 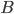 | 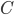 | 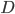 | 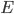 | 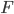 |
Abbildung von Buchstaben/Zeichen aus dem Alphabet mit 15 Buchstaben und der Null auf einstellige Zahlen/Symbole in 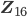 – wie beim Hexadezimalsystem
– wie beim Hexadezimalsystem
Rike Okay, nicht schlecht, ihr nehmt Sonderzeichen für die zweistelligen Zahlen.
Paula Ja, A steht für 10, beim Umrechnen in das Dezimalsystem benutzen wir anstelle des A natürlich die 10.
Rike Ja, ja, B steht für 11 und immer so weiter.
Bezug zum RSA-Algorithmus
Paula Außerdem brauchen wir für die eigentliche Chiffrierung eine Zahl  , die möglichst groß ist und Produkt von zwei verschiedenen Primzahlen ist:
, die möglichst groß ist und Produkt von zwei verschiedenen Primzahlen ist:
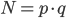
Rike Ja, ich weiß.
Paula Nehmen wir mal für den Anfang
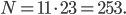
Dann können wir 253 verschiedene Wörter chiffrieren. Wir rechnen nämlich im Restklassenring 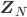 modulo
modulo  .
.
Rike Gut, das ist der RSA-Algorithmus. Doch welche Wörter lasst ihr zu?
Paula Rike, das ist genau der Punkt, den ich dir erzählen will. In Abhängigkeit von  berechnen wir die Blocklänge
berechnen wir die Blocklänge  für die Wörter. Pass auf, nehmen wir mal zu
für die Wörter. Pass auf, nehmen wir mal zu
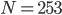
das kleinstmögliche Alphabet, das nur aus der Null und einem Buchstaben besteht. Das transferiere ich in das Binärsystem:
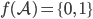
Rike Schön, schön.
Paula Dann haben wir
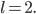
Wegen
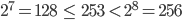
können wir 128 7-stellige Wörter aus 2 Zeichen bilden oder 256 8-stellige. Bei den 8-stelligen Wörtern hätten wir mehr Wörter als unser Raum 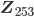 zulässt, also nehmen wir nur 7-stellige, und zwar:
zulässt, also nehmen wir nur 7-stellige, und zwar:
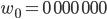
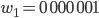
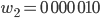

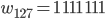
Rike Verstehe, erinnert mich irgendwie an Turing.
Berechnung der Blocklänge k und der Anzahl m darstellbarer Wörter
Paula Haha. Jetzt kommt mein Problem: Die zulässige Blocklänge  kannst du berechnen durch
kannst du berechnen durch
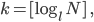
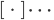 ist der ganze Anteil einer reellen Zahl. Außerdem soll die Variable
ist der ganze Anteil einer reellen Zahl. Außerdem soll die Variable 
für die Anzahl der Wörter stehen, die man mit der Blocklänge  aus dem Alphabet mit der Länge
aus dem Alphabet mit der Länge  berechnen kann:
berechnen kann:
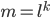
Hier im Beispiel ist
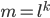
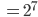
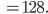
Rike Okay, verstehe. Nur ist das Alphabet mit 2 Zeichen sehr kurz und der Wortschatz aus 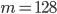 Wörtern ist sehr klein, es ist ungefähr die Hälfte von
Wörtern ist sehr klein, es ist ungefähr die Hälfte von 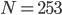 . Bei Effie Briest waren die häufigsten 128 Wörter fast nur Füllwörter und die Namen der Hauptpersonen, damit kann man keine Inhalte vermitteln.
. Bei Effie Briest waren die häufigsten 128 Wörter fast nur Füllwörter und die Namen der Hauptpersonen, damit kann man keine Inhalte vermitteln.
Paula Stimmt. Das binäre System hat sehr wenig mit unserer Sprache zu tun. Also habe ich bei festem
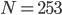
das Alphabet immer länger gemacht, ich habe die Blocklänge berechnet und die Anzahl darstellbarer Wörter. Bei der Blocklänge 1 habe ich aufgehört.
Rike Okay, dann bestehen die Wörter aus nur einem Buchstaben, ja, da hätte ich auch aufgehört. Zeig mal!
Paula Hier!
Diskussion der Funktionen m(l) und k(l)
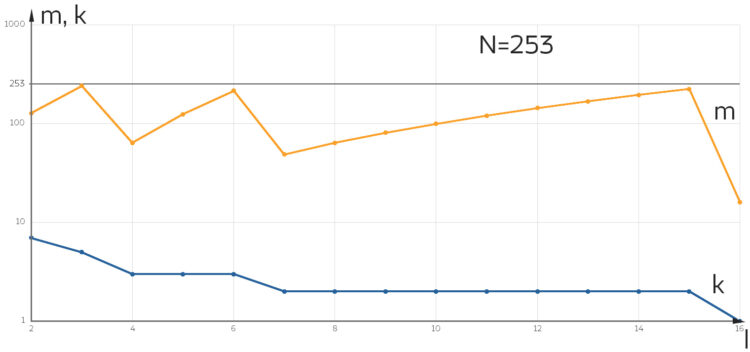
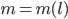 (orange) der Anzahl darstellbarer Wörter in
(orange) der Anzahl darstellbarer Wörter in 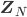 und der Blocklänge
und der Blocklänge 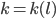 (blau) in Abhängigkeit von der Länge des Alphabets
(blau) in Abhängigkeit von der Länge des Alphabets  .
.Rike Hmm. Da siehst du, dass es gut ist, weitere Alphabete zu testen. Die Anzahl der darstellbaren Wörter wird schon bei 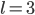 viel größer. Wie groß sind denn diese Maxima?
viel größer. Wie groß sind denn diese Maxima?
Paula Warte, die Werte sind
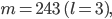
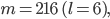
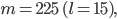
also wenig kleiner als  . Ich finde die Form der
. Ich finde die Form der  -Kurve sehr merkwürdig, ich kann das nicht verstehen!
-Kurve sehr merkwürdig, ich kann das nicht verstehen!
Rike Das ist wohl so ein typisches Diskrete-Mathe-Phänomen!?
Paula ???
Rike Ja, warte mal, zunächst haben wir eure Funktion
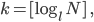
die bildet eigentlich nur die natürlichen Zahlen  , die größer als 1 sind, in die natürlichen Zahlen ab:
, die größer als 1 sind, in die natürlichen Zahlen ab:

Wenn du erstmal mit einer Funktion, na, nennen wir die mal 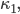 startest, die die Blocklänge für reelle Zahlen
startest, die die Blocklänge für reelle Zahlen  ohne Diskretisierung berechnest:
ohne Diskretisierung berechnest:
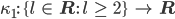
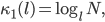
dann kriegst du eine streng monoton fallende und stetige Funktion 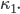
Paula Ich soll mir ein Alphabet mit 2.1, 2.5 oder 2.99 Buchstaben vorstellen? Das ist nicht implementierbar! Weißt du, hier in München sind alle ganz bodenständig, Teile von Buchstaben gibt es hier nicht. Für mich ist die Welt diskret.
Rike Paula, ist ja gut. Bei reellen Funktionen kannst du aber viel besser Stetigkeit, Differenzierbarkeit und Monotonie diskutieren. Außerdem wäre es gut, Funktionen nicht immer sofort zu interpretieren und aus dem Modell heraus zu argumentieren, sondern einfach mal die Funktionen als Funktionen an sich stehen zu lassen.
Paula Na gut, aber nur, weil du meine Schwester bist.
Rike Danke! Wenn wir jetzt  weiterhin reell und größer gleich 2 nehmen und dann den ganzen Anteil von
weiterhin reell und größer gleich 2 nehmen und dann den ganzen Anteil von 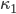 berechnen, das wäre dann die Funktion
berechnen, das wäre dann die Funktion 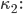
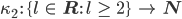
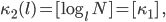
dann haben wir eine unstetige Funktion.
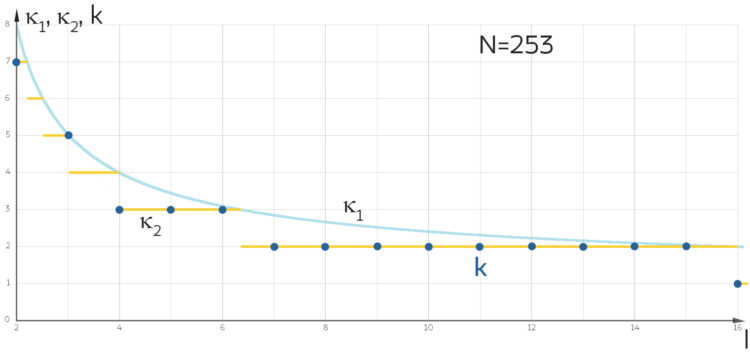
 (blaue Punkte),
(blaue Punkte), 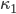 (hellblau),
(hellblau), 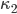 (gelb) für die Blocklänge in Abhängigkeit der Länge
(gelb) für die Blocklänge in Abhängigkeit der Länge  des Alphabets.
des Alphabets.Paula Aber immer noch monoton fallend, wenn auch nicht streng.
Rike Stimmt. Sie hat jetzt ein paar Sprünge und ist stückweise konstant. Wenn wir jetzt die Funktion
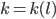
für die natürlichen Zahlen 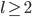 betrachten, dann erhalten wir nur noch diskrete Werte für
betrachten, dann erhalten wir nur noch diskrete Werte für  und
und  . Außerdem werden gar nicht alle Werte angenommen: so für
. Außerdem werden gar nicht alle Werte angenommen: so für 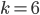 und
und 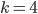 . Das Wesen von
. Das Wesen von 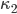 , diese Sprünge und sonst stückweise konstant zu sein, bleibt erhalten.
, diese Sprünge und sonst stückweise konstant zu sein, bleibt erhalten.
Die Potenzfunktion m
Paula Richtig. Wenn wir die Werte für  in die Funktion
in die Funktion
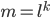
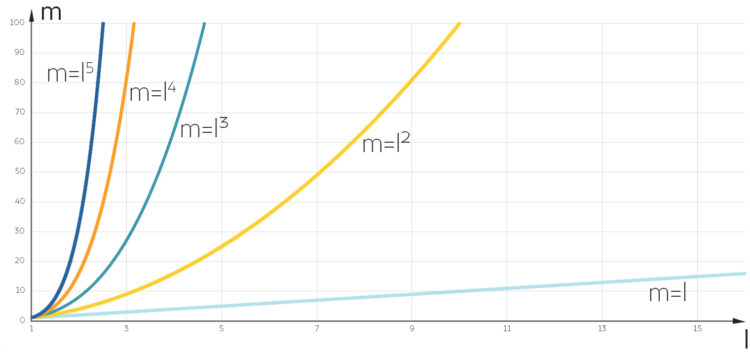
einsetzen, die für festes 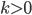 streng monoton wachsend wäre, dann kommen wir zu so dieser merkwürdigen Sägezahnkurve, weil
streng monoton wachsend wäre, dann kommen wir zu so dieser merkwürdigen Sägezahnkurve, weil  zwar positiv, aber nicht konstant ist.
zwar positiv, aber nicht konstant ist.
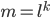 für verschiedene feste
für verschiedene feste  .
.Rike Schau doch mal genauer hin, Paula, solange  sich nicht ändert, wächst die Kurve
sich nicht ändert, wächst die Kurve  . Wenn bei festem
. Wenn bei festem 
 kleiner wird , wird auch
kleiner wird , wird auch  kleiner.
kleiner.
Paula Haha, ich sehe schon, meine Schwester durchschaut alles.
***
Übungsaufgaben
- Berechne die Kurven
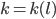 und
und 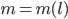 für ein größeres
für ein größeres  .
. - Ist
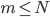 ?
? - Wie groß kann
 sinnvollerweise werden? Was wird aus
sinnvollerweise werden? Was wird aus 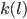 und
und 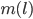 für große
für große  ?
?
Lösungen
1. Für
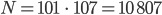
erhält man:
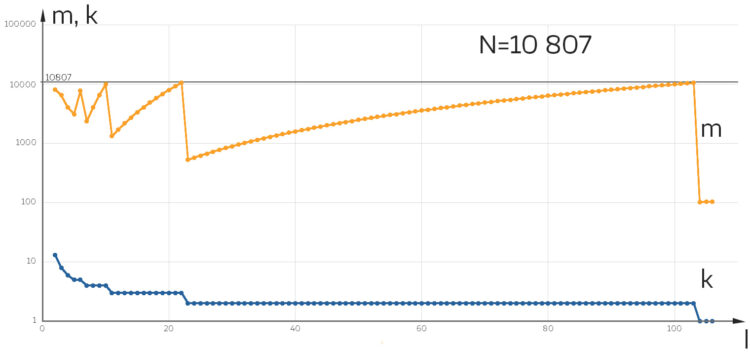
 (orange) und
(orange) und  (blau) für
(blau) für 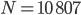 .
.
2. Ja, weil
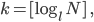
ist
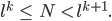
Und weil
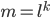
ist, ergibt sich
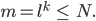
3. Es sollte 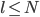 sein. Dann hat für große
sein. Dann hat für große  jedes Wort nur ein Zeichen/Buchstaben. Offensichtlich gelten
jedes Wort nur ein Zeichen/Buchstaben. Offensichtlich gelten
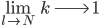
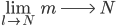
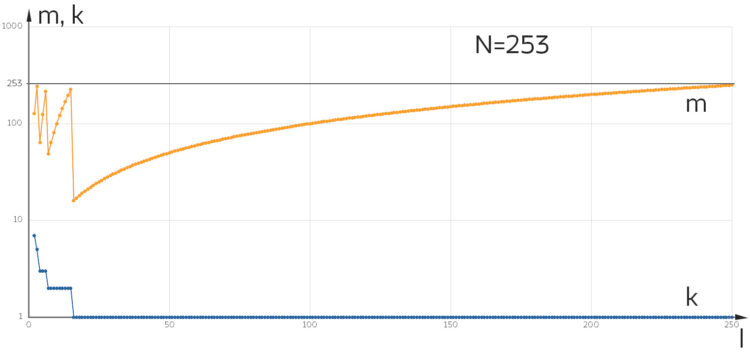
 (orange) und
(orange) und  (blau) für große
(blau) für große  ‘s, dh. für "Alphabete" mit mehr als 20 und bis zu
‘s, dh. für "Alphabete" mit mehr als 20 und bis zu 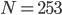 "Buchstaben".
"Buchstaben".
