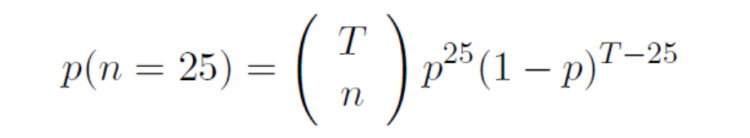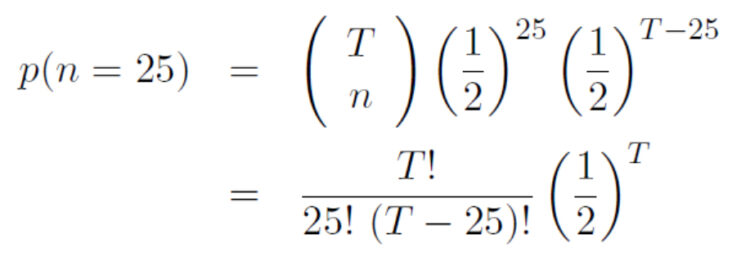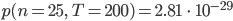Rike hat ein spezielles Roulette für die langen Winterabende am Nord-Ostsee-Kanal vorgeschlagen. Ihre Roulette-Maschine hat 100 Nummernfächer (1 – 100). Außerdem gibt es zwei Urnen mit insgesamt 100 Kugeln, durchnummeriert von 1 bis 100: Eine für Charly mit zufällig ausgewählten 25 Kugeln und eine Urne für Rike mit den restlichen 75 Kugeln. Ben ist heute Croupier und bedient die Roulette-Maschine. Wenn nach dem Werfen der Kugel diese in ein Nummernfach fällt, zB die 17, dann muss die Kugel mit dieser Nummer die Urne wechseln. Es gewinnt, wer die meisten Kugeln hat.
Das Roulette-Spiel

Nach und nach leert sich Rikes Urne, weil es ja viel wahrscheinlicher ist, dass die geworfene Zahl in ihrer Urne ist, und nach und nach füllt sich Charlys. Schließlich haben beide ca. 50 Kugeln. Als Charly mal etwas mehr hat, gibt Rike auf und lässt Charly gewinnen.
Charly Na, so interessant war es auch nicht! Alles strebt zum Gleichgewicht.
Rike Haha, genau das will ich mit euch diskutieren. Ich habe mir überlegt: Das Verhalten kann man gut simulieren: Nennen wir mal  die Zahl, mit der ich außerhalb des Gleichgewichtes starte.
die Zahl, mit der ich außerhalb des Gleichgewichtes starte.
Charly Okay,  ist der Überschuss:
ist der Überschuss:

Rikes analytisches Modell
Rike Ja, richtig, Überschuss oder Surplus-Wert. Er könnte natürlich auch anders sein. Die Wahrscheinlichkeit 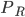 , eine zufällige Zahl von 100 aus meiner Urne zu erhalten, ist
, eine zufällige Zahl von 100 aus meiner Urne zu erhalten, ist
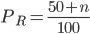
und die Wahrscheinlichkeit, eine Zahl aus deiner Urne zu erhalten, ist
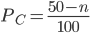
Charly Okay.
Rike Die Änderung des Surpluswertes nach jedem Wurf (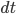 ) ergibt sich aus der Wegnahme einer Kugel mit der Wahrscheinlichkeit
) ergibt sich aus der Wegnahme einer Kugel mit der Wahrscheinlichkeit 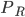 und der Hinzunahme einer Kugel mit der Wahrscheinlichkeit
und der Hinzunahme einer Kugel mit der Wahrscheinlichkeit 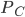 , also:
, also:
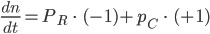
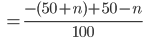
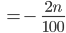
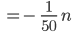
Charly Hey! Ich habe es geahnt! Schon wieder Differentialgleichungen! Exponentielles Lösungsverhalten!
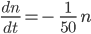
Dann haben wir noch den Vorteilsanfangswert von Rike:
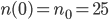
1 - 2 - 3, dann haben wir
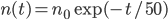
Von diesen Exponentialfunktionen kommen wir gar nicht weg im Augenblick, was?
Rike Haha!
Bens Schritt-für-Schritt-Zufalls-Modell
Ben Ach wisst ihr, ihr habt den Zufall so gar nicht richtig drin. Am Ende kriegt ihr eine deterministische Lösung raus, aber so geht das Spiel gar nicht! Ich programmiere das mal Schritt für Schritt, jeder Wurf eine zufällige Zahl mit einem Zufallsgenerator. Hier schaut mal! Wie viele Würfe wollt ihr denn?
Charly Na, 100?!
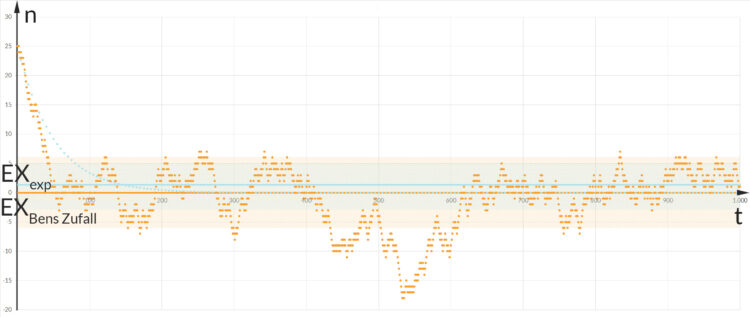
Ben Okay, lasst uns 100 Würfe machen und die beiden Funktionen vergleichen:
 aus der Dgl. in Hellblau und der Schritt-für-Schritt-Zufalls-Verlauf in Orange für jeweils 100 Würfen.
aus der Dgl. in Hellblau und der Schritt-für-Schritt-Zufalls-Verlauf in Orange für jeweils 100 Würfen.Charly Das Ergebnis der Exponentialfunktion geht früher oder später zu Null, aber sie lässt nicht zu, dass  negativ wird, dass ich gewinne. Hmm???? Ben, kannst Du das auch noch länger simulieren? 200 Würfe?
negativ wird, dass ich gewinne. Hmm???? Ben, kannst Du das auch noch länger simulieren? 200 Würfe?
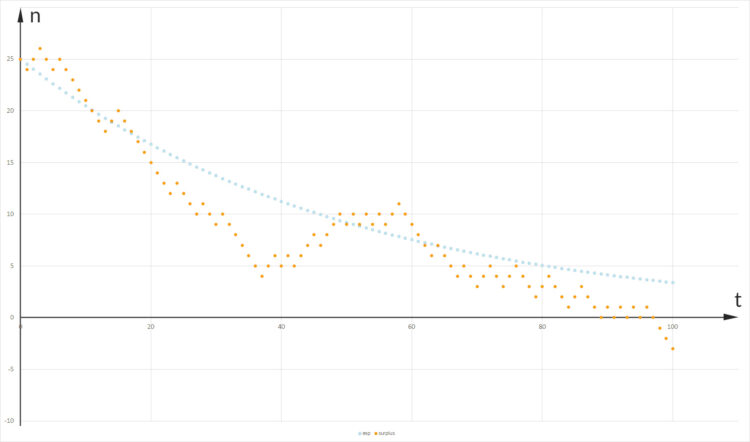
Ben Na klar! Hier!
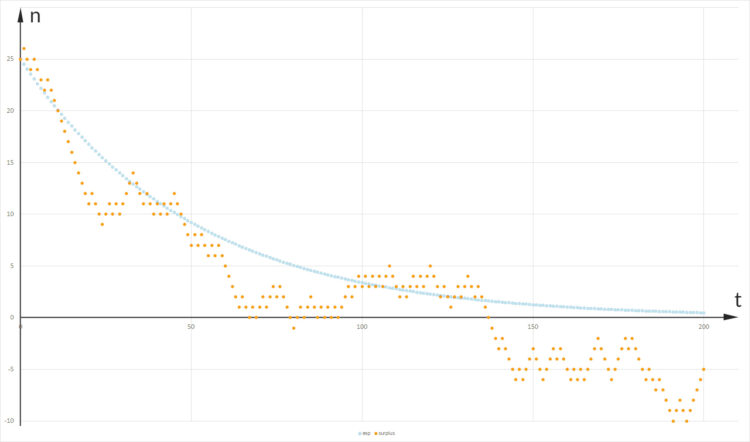
Rike Hmm, die beiden Funktionen sind wirklich verschieden. Die Simulation Schritt für Schritt mit einer Zufallszahl passt besser zum Spiel. Kannst du mal den Mittelwert und die Varianz ausrechnen?
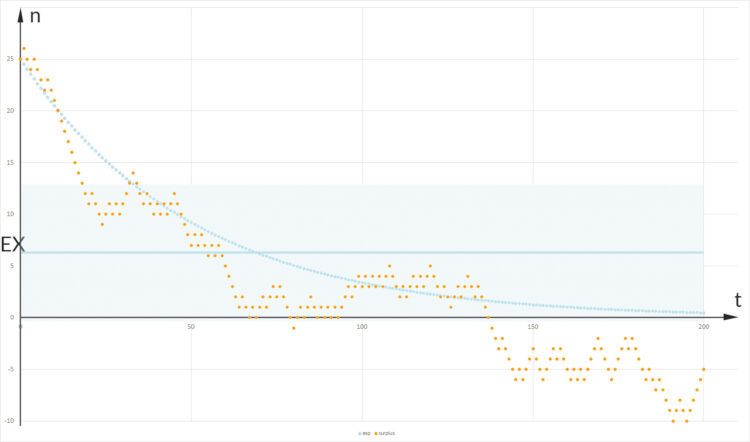
Ben Na klar! Der Mittelwert ist natürlich von der Anzahl der Würfe abhängig. Am Anfang ist  nahe 25, da ist der Erwartungswert für wenige Würfe recht hoch, später wird er kleiner.
nahe 25, da ist der Erwartungswert für wenige Würfe recht hoch, später wird er kleiner.
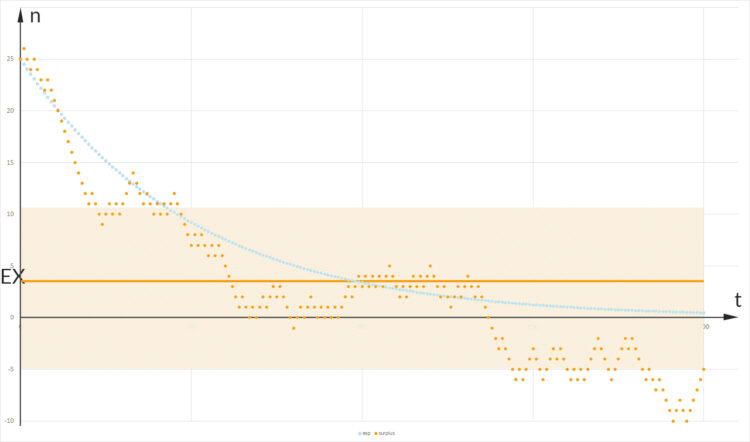
Rike Hmm, bei der Exponentialfunktion bleibt der Mittelwert immer positiv, das passt nicht zum Spiel. Ben, du hast recht.
Bens physikalisch zeitliche Interpretation
Ben Wisst ihr, mit der Zufallssimulation kommen wir nach ca. 100 Würfen zu der Stelle, wo  nahe Null ist. Dann ist die Wahrscheinlichkeit, dass eine geworfene Zahl in einer Urne ist, ca. ½. Das heißt, es ist genauso wahrscheinlich, dass sie in Rikes Urne ist wie in Charlys. Der einzelnen Kugel ist es „egal“, in welcher Urne sie ist. Wenn das jetzt mal Teilchen in einem Volumen wären, wo jedes eine gewisse Geschwindigkeit hätte und die zusammen eine mittlere Geschwindigkeit haben, eine Temperatur letztlich, dann wären die beiden Inhalte nahe des Gleichgewichtes gleich warm. Und mikroskopisch wechselt immerzu die Teilchen aus der einen Urne in die andere Urne. Das wäre kein Problem.
nahe Null ist. Dann ist die Wahrscheinlichkeit, dass eine geworfene Zahl in einer Urne ist, ca. ½. Das heißt, es ist genauso wahrscheinlich, dass sie in Rikes Urne ist wie in Charlys. Der einzelnen Kugel ist es „egal“, in welcher Urne sie ist. Wenn das jetzt mal Teilchen in einem Volumen wären, wo jedes eine gewisse Geschwindigkeit hätte und die zusammen eine mittlere Geschwindigkeit haben, eine Temperatur letztlich, dann wären die beiden Inhalte nahe des Gleichgewichtes gleich warm. Und mikroskopisch wechselt immerzu die Teilchen aus der einen Urne in die andere Urne. Das wäre kein Problem.
Symmetrie der Zeit
Rike Aha! Die Wärmeleitung vom Warmen zum Kalten und umgekehrt?
Ben Ja, genau. Die Temeperatur ist nur ein Mittelwert – die Teilchen selbst haben ganz unterschiedliche Werte. Genauso ist es bei der Urne: Wir haben einen Mittelwert für den Surplus-Wert, aber der augenblickliche Surplus-Wert ist anders. Jetzt lass uns mal überlegen, ob wir aus dem Gleichgewicht nicht nur mikroskopisch wieder rauskommen sondern makroskopisch?
Charly Was meinst du?
Ben Na, ob wir sich Temperatur in einem Gefäß erhöht und im Nachbargefäß wird sie kleiner. Haha! Beim Roulette ist das so: Wir starten jetzt mal mit

das heißt, in jeder Urne sind 50 Kugeln. Wie groß ist die Wahrscheinlichkeit, dass ich nach 100 Würfen zu

komme?
Rike Warte mal, die Wahrscheinlichkeit 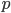 , bei einem Roulette-Wurf eine Zahl zu erhalten, die zu einer Kugel aus Charlys Urne gehört, ist ½:
, bei einem Roulette-Wurf eine Zahl zu erhalten, die zu einer Kugel aus Charlys Urne gehört, ist ½:
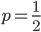
Die Wahrscheinlichkeit, 25 Mal eine Kugel aus Charlys Urne zu treffen, kriegen wir dann mit der Binomialverteilung:
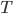 ... ist die Anzahl der Würfe.
... ist die Anzahl der Würfe.
Stimmt's?
Charly Sagt mal, ihr kennt euch aber gut aus? Ich versuche mal, das auszurechen:
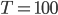
kriege ich dann
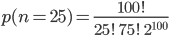
Hmm??? Das kann kein Taschenrechner!
Ben Na hör mal! Taschenrechner! Mit was Anderem kriegst du das doch hin!
Charly Okay, ich kürze geschickt, vielleicht kriege ich das mit Python hin …. okay, … wartet ... – das ergibt
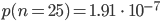
Hey, das ist ja wirklich sehr klein! Wenn das Spiel im Gleichgewicht ist, kommt es niemals zu dem Anfangswert zurück? Wenn Rike und ich das Spiel mit 50:50 starten und eine Milliarde Mal spielen, dann kommt in 191 Fällen 75:25 raus? Sagt mal –?!
Rike Haha, wir spielen das jetzt nicht eine Milliarde Mal! Charly, unser Modell hat einen prinzipiellen Fehler: Unser erster Anfangswert ist so unwahrscheinlich, er ist so unnatürlich! Wir waren so stark aus dem Gleichgewicht, dass der natürliche Prozess vom gleichmäßigen Austausch im Mikroskopischen gestört war. Es macht keinen Sinn, hier von der Umkehrbarkeit der Zeit zu reden.
Charly Hmm, habe ich was nicht mitbekommen?
Ben Haha, wir zeigen dir morgen mal die Arbeiten von Wheeler: Frontiers of Time!
***
Übungsaufgaben
- Berechne
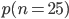 für
für 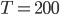 .
. - Berechne die Erwartungswerte und Varianzen für beide Funktionen (die Exponentialfunktion und eine Schritt-für-Schritt-Zufalls-Berechnung für)
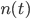 und große
und große 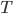 .
.
Lösungen