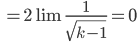Skip to main content


Zutaten: Zucker, Kakaomasse (50%), Milchzucker, Weizenmehl, Vollmilchpulver, Magermilchpulver, Butterreinfett, Sahnepulver, Butter (1,4%)
Kann Spuren von Analysis und Geometrie enthalten.

2020_20-immer-schneller-titel

Wie man mit Mathematik immer schneller wird

Marietta Ehret Analysis, Differenzialgleichungen

Rike, Miriam und Ben sitzen immer noch über der Wellengleichung zusammen.

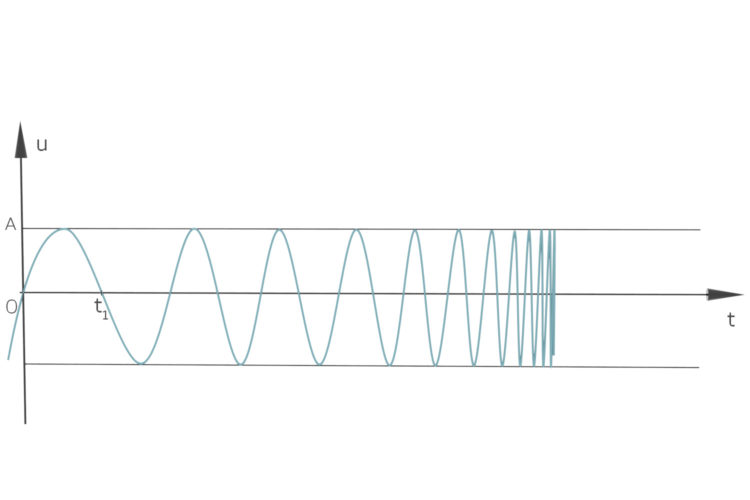
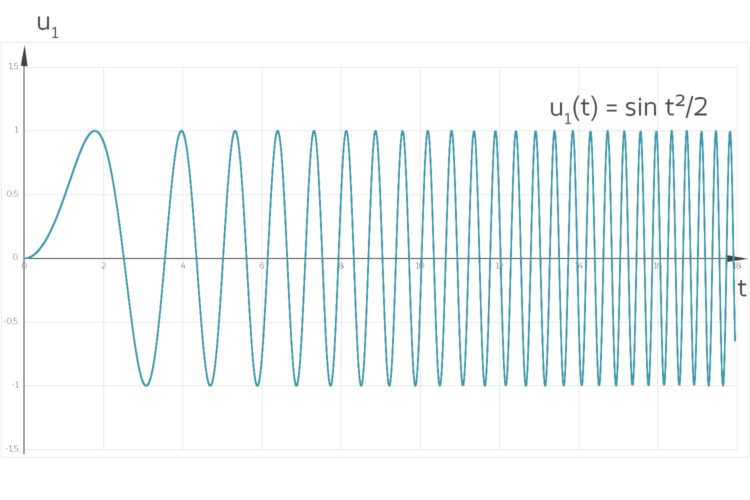
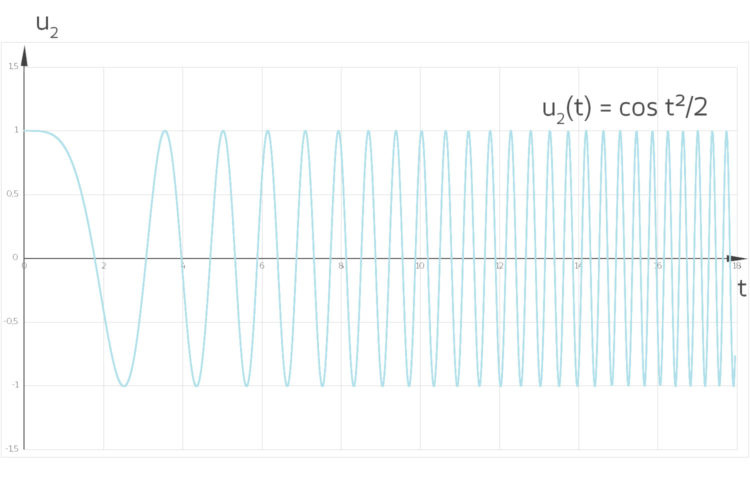
Miriam Mein Freund Ariel hat für mich am Mischpult einen Ton erzeugt, der immer höher wurde, schaut mal, der sieht so aus:

20_sinus_kurve_02_hoeher_arnold_01-11

Da fing mein Interesse an. In Israel habe ich ein paar Leute gefragt, was das für Funktionen sind, aber keiner wusste das. Sie meinten, ich wäre crazy. Doch jetzt bin ich hier in Berlin und hoffe, dass sich das Geheimnis lüftet.

Veränderliche Frequenzen

Rike Wir hatten ja schon die stehenden Wellen, aber Töne, die ihre Frequenz ändern, genügen nicht der homogegenen Wellengleichung ….

Da muss die Frequenz zeitlich veränderlich sein:

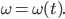
Wie wäre es, wenn wir für den Fall, dass die Frequenz wächst, den Ansatz

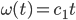
machen? Dann kriegen wir für die zeitlichen Schwingungen

20_sinus_kurve_06_arnold_01-07
okay?

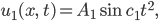
Miriam Okay! Sounds good to me.

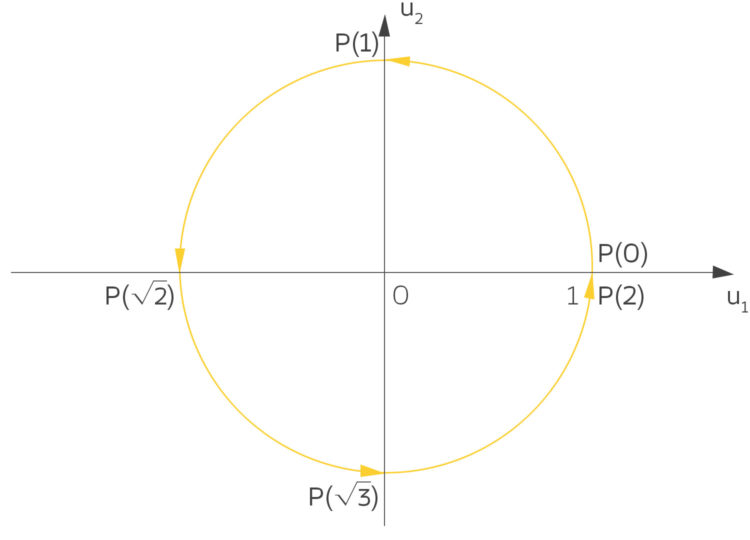
Ben Rike, kannst du nicht Sinus und Kosinus als Kreis betrachten – eben im Phasenraum?

Rike Ja, klar! Ich lasse mal ein paar Konstanten weg und nehme

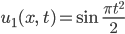
und dazu die spezielle Kosinus-Funktion:

20_cos_kurve_06_arnold_01-07

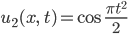
Nullstellen für u1 und u2

Die Nullstellen für u1 sind dort, wo

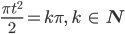
also für

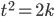
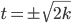
Für u2 sind finden wir die Nullstellen genauso

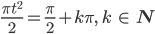
folglich

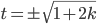
Schwingungen im Phasenraum

Ich habe bei beiden dieselbe Amplitude 1. Lasst mich mal wie vorhin zur Zeit t den Punkt

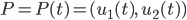
zeichnen. Dann kriege ich wieder einen Kreis:

20_16_cos-sin-keise_06-10

Wenn ich nacheinander ausrechne, wann ich bei den Punkten für 90°, 180°, 270° oder 360° ankomme, so wie bei den Nullstellen (, nach einer Viertelrunde habe ich nämlich

 

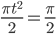
also

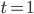
usw.), dann versteht ihr, dass ich für den ersten Viertelkreis 1 Zeiteinheit benötige, für den zweiten 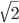, für den dritten 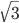und für den ganzen Kreis 2 Zeiteinheiten. Jetzt merkt ihr schon, dass ich immer schneller werde.

Zeit für eine "Runde"

Miriam Wie schnell kannst du denn überhaupt werden? Gibt es eine Grenze?

Ben Eine Art Lichtgeschwindigkeit?

Rike Gute Frage! Ich nehme mal einen vollständigen Kreis vom und zum Punkt (1, 0): Das ergibt 2kπ als Argument und das löse ich nach meiner quadratischen Zeit auf:

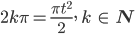
Das ergibt wiederum

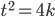
oder

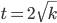
Für die erste Runde brauche ich

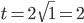
Zeiteinheiten. Für die ersten zwei Runden

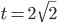
Zeiteinheiten. Für die ersten k Runden

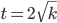
Um die Zeit nur für eine Runde auszurechnen, muss ich die Differenz berechnen, das gibt für die k-te Runde:

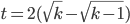
Hmm, das ist schon mal eine Herausforderung. Wenn k sehr groß wird, kriege ich: Unendlich minus Unendlich! Das steht in jedem Analysisbuch, ein paar Standardumformungen, l’Hospitalsches Gesetz, und diese Differenz geht nach Null. Das heißt, für die allerletzte Runde brauche ich gar keine Zeit! Aber das ist ja die Hölle – jetzt mal aus sportlicher Sicht!

Miriam Ich kann es mir nicht vorstellen!

Rike Okay, nehmen wir mal an, ich brauche für die erste Runde eine Stunde – das sind 60 Minuten oder 3.600 Sekunden. Wenn ich immer nach dem Gesetz (u1(t), u2(t)) im Kreis laufe, und ich laufe eigentlich ganz gern, wenn ich nicht Mathe mache, dann brauche ich für die 1-millionste Runde

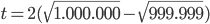
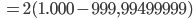
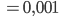
Zeiteinheiten, das heißt ein Tausendstel einer Stunde, das sind 3,6 Sekunden!

Miriam Sehr sportlich!

Ben Hahaha!

***

Übungsaufgaben

  1. Welche Wellengleichung lösen u1 und u2?
  2. Berechne den Grenzwert

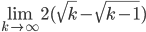
Lösungen

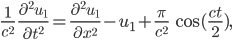
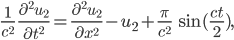
  1. mit

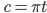
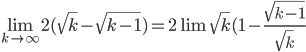
  2. = "0/0" ~ l’Hospitalsches Gesetz ... vereinfachen ...