Rike und Ben haben Miriam in Berlin kennengelernt. Sie kommt aus Tel Aviv und will Tonmeisterin werden.
Ben Hi, Miriam!
Rike Hi, Miriam, wie geht es dir?
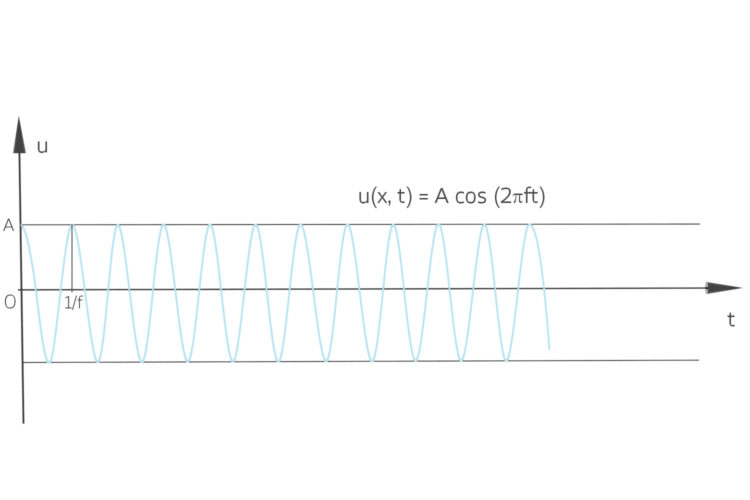
Miriam Hi, Rike und Ben, wie geht es euch? Ben hat mir deine Geschichte vom Sinus erzählt. Wir hatten in Israel auch den Sinus in der Schule. Es stimmt, wir haben nur wenige Werte berechnet. Als mich einmal der Freund der Familie, Ariel, zu einer offenen Probe und Konzert einlud, durfte ich ihm am Mischpult über die Schulter schauen. Da hat er mir different sinus curves gezeigt – o mein Deutsch! Das hat mir gut gefallen, und jetzt haben wir jeden Tag mit Sinus-Funktionen zu tun. Schaut mal, so sieht die Grundschwingung einer Flöte beim Ton A (440 Hz) aus:
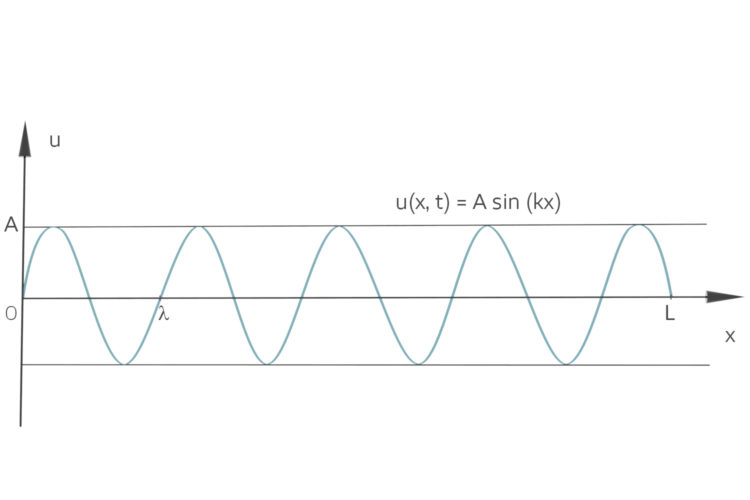
Schwingung in Raum und Zeit für eine Saite der Gitarre
Dazu kommen noch Oberwellen, die die Klangfarbe ausmachen. Wenn ich mit meiner Gitarre das d anschlage, dann habe ich f=146 Hz und mit der Bassgitarre erhält man das tiefe E mit der Frequenz f = 82 Hz. Die Lautstärke wird durch die Höhe der Schwingung, die Amplitude, ausgedrückt. Die Wellenlänge λ kriege ich aus
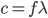
c ist die Ausbreitungsgeschwindigkeit der Welle.
Ich finde es wunderfull, dass Töne messbar sind und kontrolliert generiert werden können, diese Sinus-Funktionen begleiten mich. Ich kann acoustic properties gut verstehen, aber die Mathematik ist nicht einfach für mich. Schwingungen in Raum und Zeit zu verstehen ist nicht einfach. Am Mischpult sehe ich ja nur die zeitlichen Schwingungen mit ihren Frequenzen im Spektrum.
Eindimensionale Wellengleichung
Rike Hey Miriam, gut, dass du hier bist. Das Sinus-Problem ist nicht schwer. Jede Schwingung ist Lösung der Wellengleichung:
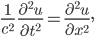
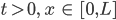
Lösungsansatz
Als Lösung erhält man dann Sinus- und Kosinusschwingungen in Raum und Zeit, x und t:
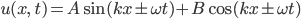
das weißt du ja schon. A ist die Amplitude, ω die Kreisfrequenz, die Tonmeister nehmen immer f statt ω, aber das ist kein Problem:
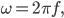
es ist eine Art Skalierung.
Wenn du dann den Ansatz in die Wellengleichung einsetzt, kriegst du die Bedingung
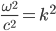
oder
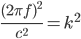
oder
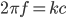
So kriegst du unendlich viele Lösungen, die kannst du nach den Wellenzahlen k oder den Frequenzen f sortieren.
Miriam Okay, aber wir können nicht alle hören.
Randbedingungen
Rike Stimmt, wir sind noch nicht fertig. Wir haben die Länge von Bens Flöte oder der Gitarrensaiten noch nicht benutzt. Also, wenn wir jetzt noch die üblichen Randbedingungen vorschreiben:
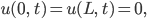
das heißt, am Rand gibt es keine Auslenkung, dann kriegen wir einen Zusammenhang von der Wellenzahl k und der Länge L. Lass mich mal nur die Sinuswellen nehmen, dann hätten wir 2 Lösungen
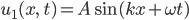
und
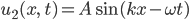
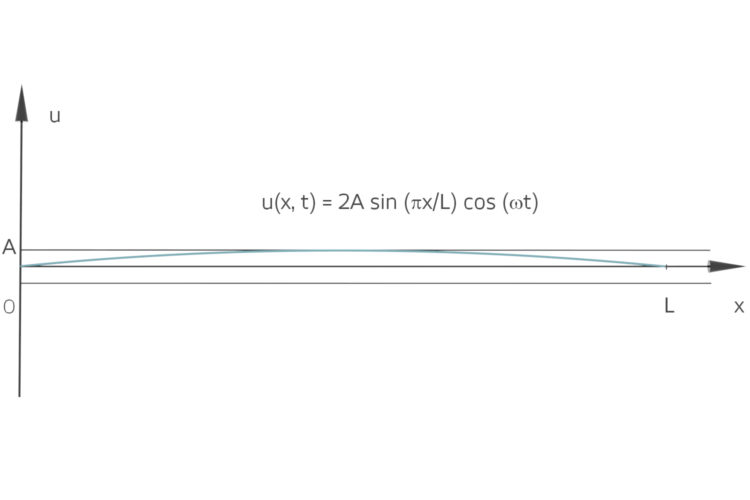
Ihre Summe – also die Überlagerung der beiden Wellen mit derselben Amplitude – ergibt:
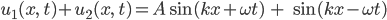
Mit einem Additionstheorem für den Sinus kriegst du dann:
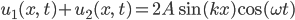
Miriam Hey, das sieht gut aus, für x = 0 wird das Null, und für x = L, warte mal, das kann ich auch:
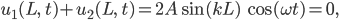
Das funktioniert nur für die Nullstellen des Sinus, hmm, jetzt wird es aber kompliziert...
Rike Schau, die Nullstellen sind bei Vielfachen von π, nehmen wir mal eine neue Variable k' für die natürlichen Vielfachen, also
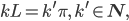
Miriam ????
Wellenzahl k
Rike Das bedeutet, dass
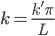
für natürliche k‘ sein muss.
Miriam Jetzt habe ich den Überblick verloren!
Rike Schau, bei der Gitarre wäre
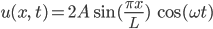
eine Lösung.
Miriam Stimmt – und k' = 1?
Zusammenfassung
Rike Ja, stimmt! Ich fasse Alles zusammen: Wir haben aus den Randbedingungen berechnet, dass
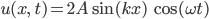
Lösung der Wellengleichung ist, falls
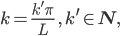
Außerdem können wir aus unserem Ansatz und der Wellengleichung die dazugehörige Frequenz f berechnen
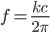
Schlussendlich bekommst du die Wellenlänge λ aus deiner Gleichung für c, λ und f:
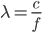
Miriam Okay, alles klar! Vielleicht hätten wir besser partial differential equations im Studium gemacht!
Ben Ja, eigentlich braucht ihr viel Mathematik, du kannst doch bestimmt die PDE-Vorlesung an einer Uni mithören?
Miriam Haha, ja bestimmt könnte ich das! Doch, wir spielen noch Instrumente, singen im Chor und nehmen Musik auf, das wird ganz schön viel!
***
Übungsaufgabe
Teste mit den anderen Schwingungen der Wellengleichungen die Randbedingungen!
