Rike und Ben sind in Urlaub an die deutsche Nordseeküste gefahren. Sie bewundern den weiten Strand. Hier fällt Rike eine Story aus ihrer (mathematischen) Kindheit ein:
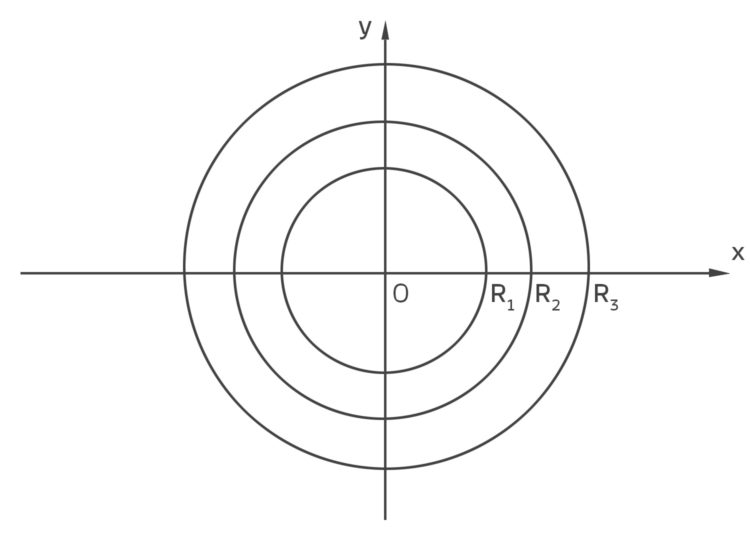
Rike Ich war immer von Kreisen fasziniert.
Die Formel ist
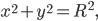
das weißt du ja.
Ben Klar!
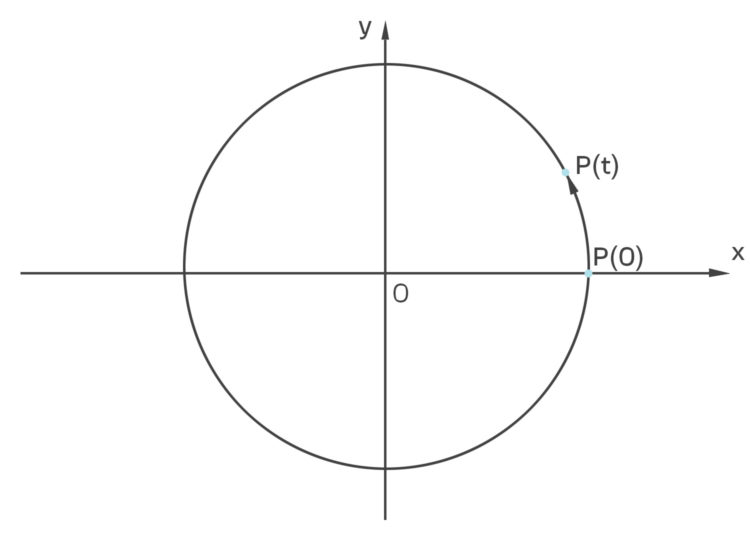
Rike Wenn du auf der Kreislinie entlanggehst mit der Zeit t, dann kommst du früher oder später zur Sinus- und Kosinusfunktion.
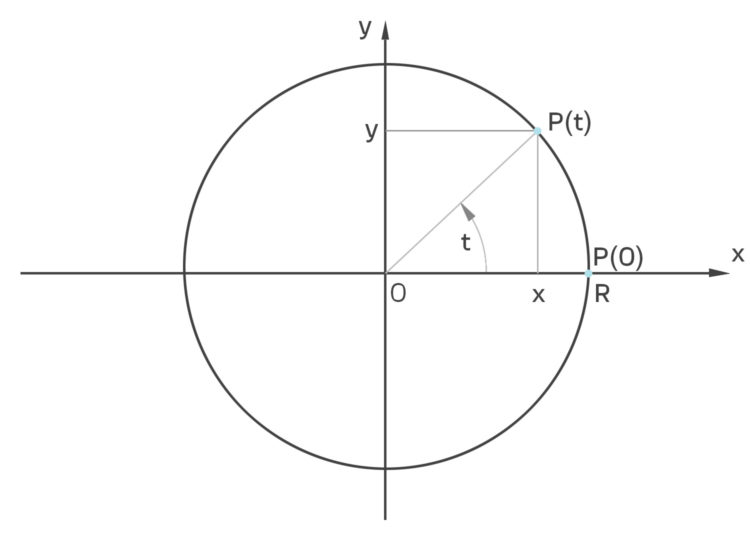
Parameterdarstellung des Kreises
Für einen Punkt P kriegen wir die Koordinaten (x, y), so:
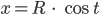
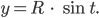
Normalerweise nimmt man für die Wanderung auf dem Kreis statt der Zeit t einen Winkel, doch die Vorstellung, auf der Kreislinie mit der Zeit herum zu laufen, ist großartig. Für einen kompletten Rundgang von
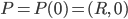
wieder zum Anfangspunkt
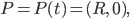
läuft man einmal herum, das sind 360° oder
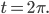
Ben Okay.
Spezielle Werte für den Sinus
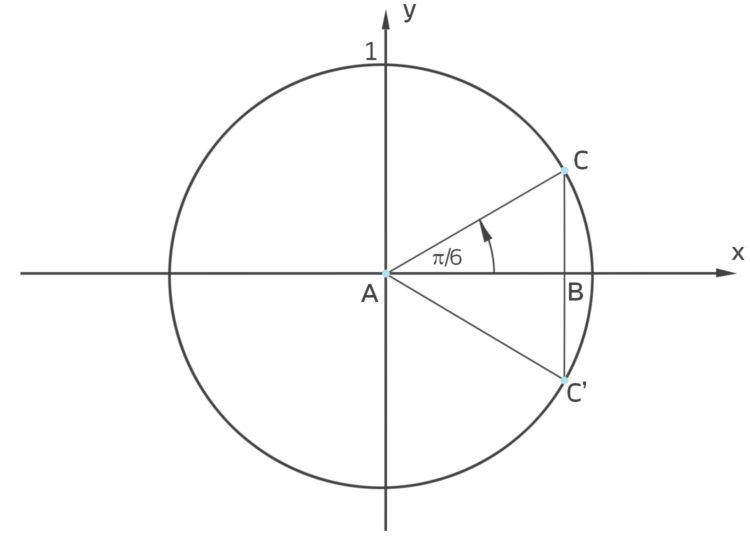
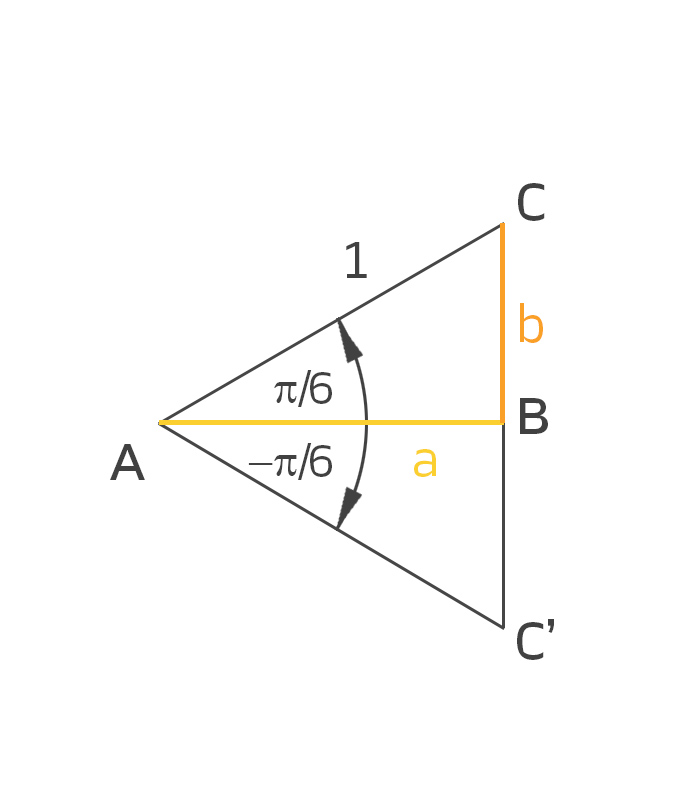
Rike Obwohl die Definition des Sinus und Kosinus mit den Längen von rechtwinkligen Dreiecken im Kreis so einfach ist, ist es schwer, die Werte wirklich zu berechnen. Wir hatten das in der Schule bei Wiezorek; und natürlich habe ich ihn gefragt, wie man das misst. Er hat mir sehr gut erklärt, dass
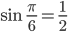
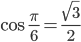
ist, weil nämlich dieses Dreieck ABC‘ ein gleichseitiges ist.
Schau mal:
Für die Seitenlänge
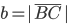
ist dann b = ½:
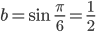
ABC ist ein rechtwinkliges Dreieck, da nehmen wir den Satz des Pythagoras:
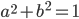
Ben Was ist a?
Rike Das ist die Länge der Strecke AB.
Ben Okay. Und weiter?
Rike Wir setzen b = ½ ein, so
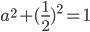
Das stellen wir nach a um:
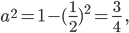
also
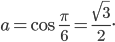
Ben Verstehe.
Sin π/7
Rike Aber für sin π/7 hatte Wiezorek keine Herleitung parat. Er hat gesagt, dass Sinus eine transzendente Funktion sei, die kann man nicht elementar berechnen! Da bin ich nach Hause gegangen, habe eine Sinus-Tabelle in einem uralten Buch gefunden, und da stand
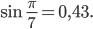
Ben Ja?
Rike Ja! Irgendwie hatte ich so eine Vorstellung von einem Gelehrten in einer Mönchskutte, der da in seiner Kammer sitzt und rechnet, aber leider hat er seine Formel mit ins Grab genommen. Tja, Taschenrechner, Internet! Aber was ist zulässig, da steht irgendeine Zahl, aber stimmt die denn, wenn es ja gar keine Formel gibt?
Ben Hm.
Rike Da habe ich mich an Wiezoreks Definition erinnert und einen Kreis in unserem größten Zimmer auf dem Fußboden gemalt. Mit dem Radius von einem Meter war der Kreis immerhin schon 2 m breit und ich musste fast 4 m² Platz schaffen. Na gut, frag‘ nicht, wie ich den Kreis gezeichnet habe. Also die Ungenauigkeit war schon wegen meiner Konstruktion bei 1 mm. Aber – ich habe für
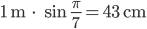
herausbekommen, also genau dasselbe wie die Tabelle:
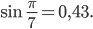
Ben Nicht schlecht! Wie alt warst du damals?
Rike Vielleicht 10, 11? Wie schon gesagt, die Millimeterangabe habe ich nicht hingekriegt. Wenn ich sin π/7 auf 5 Stellen genau bestimmen will, brauche ich eine tausendfache Vergrößerung. Also, mein Kreis sollte dann den Radius von 1 km haben, doch da bin ich mit meinen Eltern und dem Umfeld nicht weitergekommen. Aber hier könnten wir das mal probieren!
Ben Haha!
***
Übungsaufgabe
Gibt es eine Möglichkeit, sin π/7 mit 5 Stellen nach dem Komma zu berechnen?
Lösung
Mit der Potenzreihe für den Sinus
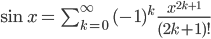
ist
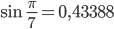
schon bei k=2.