Ben und Rike sind wieder am Nordseestrand. Heute erzählt Ben, womit er sich im Urlaub beschäftigen möchte: Er möchte endlich den Beweis von Heule et al. über die Färbung in 2 Farben der pythagoreischen Tripel in Ruhe durchgehen. Der Beweis verläuft computerunterstützt und hatte 2016 für großes Aufsehen gesorgt. Die Aufgabe geht so: Alle natürlichen Zahlen von 1 bis N werden als Kästchen gezeichnet. Diese Kästchen sollen mit 2 Farben so gefärbt werden, dass die pythagoreischen Tripel nicht einfarbig bleiben.
Rike Moment mal! Da brauchst Du erst mal eine Übersicht über die pythagoreischen Tripel!
Ben Na, für mich ist so ein Tripel eigentlich nur eine Bedingung, die erfüllt ist oder nicht: (a, b, c) ist ein pythagoreisches Tripel, a, b, c ∈ N, wenn
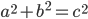
ist. (3, 4, 5) ist wegen
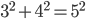
ist das bekannteste Tripel, stimmts?
Rike Okay, das kenne ich! Diese Tripel haben es in sich! Wenn du dieses eine Tripel hast, dann sind Vielfache wieder pythogoreische Tripel. So kannst du allein aus diesem Tripel (3, 4, 5) unendlich viele erzeugen. Die, die nicht Vielfache von anderen sind, heißen primitive pythagoreische Tripel.
Wenn du jedes Tripel für sich alleine nimmst, müsste es ja möglich sein, es mit 2 Farben einzufärben?
Ben Haha! Aber du sollst nicht jedes Tripel für sich nehmen. Das fängt schon bei den primitiven Tripeln an: (3, 4, 5) und (5, 12, 13) sind primitive Tripel, weil
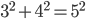
und

ist und sie ja nicht Vielfache voneinander sind. Da siehst du, dass schon die 5 in 2 Tripeln vorkommt. Jetzt kannst du die Farbe für die 5 fest setzen, die Farben von 3, 4, 12 und 13 sind dann abhängig davon.
Primitive pythagoreische Tripel
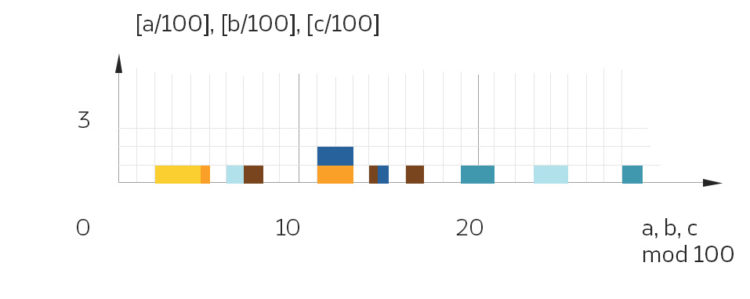
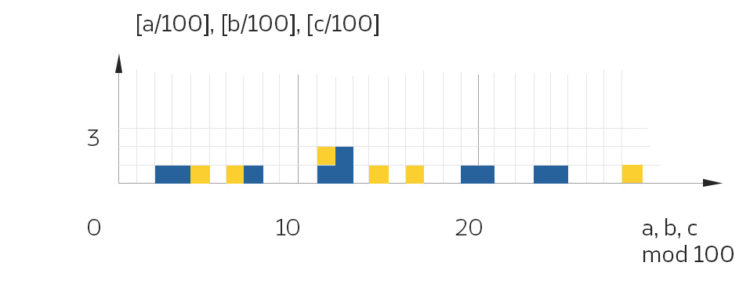
Nichtprimitive pythagoreische Tripel

Rike Aha! Brauchst Du doch wohl nur alle Möglichkeiten auszutesten! Brut-Force heißt das!
Ben Haha! Das sind viel zu viele Möglichkeiten, um sie in praktikabler Zeit zu testen. Mit Parallelrechnern – versteht sich! Heule hat ein intelligentes Verfahren gefunden. Das will ich nun genau ansehen. Und – er hat herausgefunden, dass man für alle N bis N = 7824 die Aufgabe lösen kann, aber für
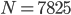
nicht. Da gibt es keine Möglichkeit der Einfärbung mit 2 Farben.
Rike Ist an der Zahl was Besonderes?
Ben Ja, Heule und Kollegen haben herausgefunden, dass die Schlüsselzahl 7825 in 2 Tripeln steckt: (625, 7800, 7825) und (5180, 5865, 7825) und dass die beiden ersten Zahlen a und b nur jeweils gleich, aber gleichzeitig verschieden eingefärbt werden müssen. Das gibt dann einen Konflikt für die dritte Zahl c = 7825. Verstehst du?
Rike Haha, hört sich witzig an!
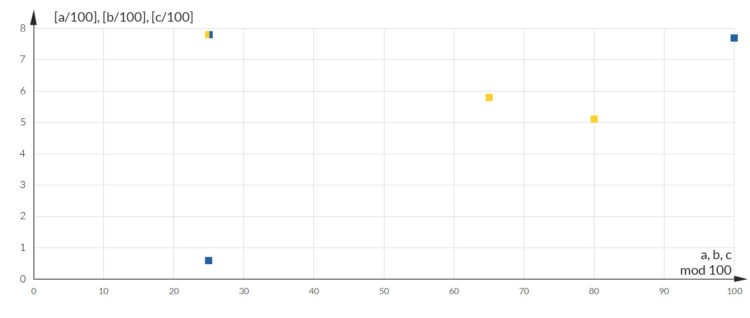
Ben Damit war das Ramsey-Problem gelöst. Ramsey hatte es 1980 ausgeschrieben und 100 USD ausgesetzt. Heule hat 4 CPU-Jahre gerechnet und die 100 USD bekommen!
Rike Hey! 100 USD! Wie geht das mit dem Einfärben?
Boolsche Variablen
Ben Er hat natürlich erst n a c h der Lösung des Problems seine berühmte 2-farbige Zeichnung erstellt. Vorher hat er es formalisiert. Vor allem die Aussage, dass für N = 7825 keine Färbung der Tripel möglich ist, ist sehr aufwendig. Du musst zeigen, dass jede Färbung zum Widerspruch führt.
Rike Und wie hat er das gemacht?
Ben Er hat wie ein echter Logiker gedacht und die Aufgabe in logischen Ausdrücken notiert und in solche umgewandelt. Zuerst nimmt er die Zahlen der Tripel und bezeichnet sie mit boolschen Variablen. Der Wert 0 soll angenommen werden, wenn die Zahl zur ersten Farbe gehört – sagen wir mal Gelb – und 1 für die andereFarbe – Blau. Beim ersten Tripel (3, 4, 5) wäre eine mögliche Zuordnung
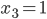
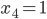
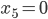
Er prüft dann für alle Tripel, ob
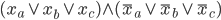
wahr ist, dann wären die Tripel nicht einfarbig. Den Obenstrich kennst du ja, ist die Verneinung.
Rike Moment! Für das Tripel (3, 4, 5) haben wir dann
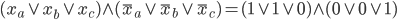
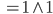
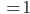
Stimmt! Sie sind nicht einfarbig. Und weiter?
Ben Sie versuchen, das Problem in einer bestimmten Form zu schreiben. Das Erste sind die boolschen Variablen 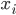 , die nur in 2 Zuständen
, die nur in 2 Zuständen 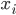 und
und  auftreten können, das Nächste sind Anweisungen.
auftreten können, das Nächste sind Anweisungen.
Rike Was sind Anweisungen in diesem Kontext?
Ben Anweisungen sind endliche Mengen von Zuständen. Wenn eine Anweisung 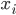 und
und  enthält, heißt sie tautologisch.
enthält, heißt sie tautologisch.
Rike Aha!
CNF-Format
Ben Heuler strebt ein bestimmtes Format von Anweisungen an: das CNF-Format: Formula Conjunction of Clauses. Das sind Vereinigungen von Anweisungen, so wie die Entscheidungsanweisung, die wir eben besprochen haben. Um die vielen Fälle systematisch zu bearbeiten, gibt es Regeln der Umformung, diese sollen natürlich das Ergebnis der Entscheidung beibehalten. So gibt es zum Beispiel die „Auflösung“ von 2 Anweisungen nach einer Variablen:
Auflösung
Wenn du 2 Anweisungen C1 und C2 mit der Variablen x in 2 Zuständen hast:
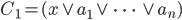
und
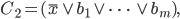
dann heißt die Anweisung C mit
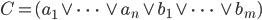
Auflösung von C1 und C2 nach x. Wenn C1 bzw. C2 logisch entscheidbar sind, dann ist auch C entscheidbar.
Rike Verstehe, dann habt ihr bestimmt auch die Addition von Anweisungen?
Erweiterungsregel
Ben Ja, klar, Rike, wenn du eine Formel F mit zwei Variablen a und b hast, dann kannst du die Variable

zu F hinzufügen, so:
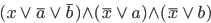
Die Entscheidbarkeit bleibt erhalten.
Unit Propagation
Wenn du eine Menge F von Anweisungen hast, dann kannst du versuchen, alle Anweisungen, die die Variablen  oder
oder 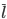 enthalten, wegzulassen. Die Variable l ist die Unit. Die neue Menge F‘ ist mit F SAT-äquivalent, d.h. beide Mengen sind entscheidbar oder beide sind nicht entscheidbar. Das machst du immer wieder, das heißt Unit Propagation.
enthalten, wegzulassen. Die Variable l ist die Unit. Die neue Menge F‘ ist mit F SAT-äquivalent, d.h. beide Mengen sind entscheidbar oder beide sind nicht entscheidbar. Das machst du immer wieder, das heißt Unit Propagation.
Rike Okay.
Ben Das Ganze läuft darauf hinaus, Anweisungen geschickt zu addieren, um einen Konflikt zu erzeugen.
Rike Hey, das erinnert mich an lineare Gleichungen, wo man mit der Determinante oder dem Rang feststellt, ob und wie viele von den Gleichungen linear abhängig sind oder nicht.
Heuristiken
Ben Stimmt! Jetzt bleibt nur noch die große Frage, welche Zustände man addiert. Findet man einen systematischen Algorithmus, wie das Gauß-Verfahren für die Mathematiker, oder geht man eher zufällig vor? Diese Entscheidungen nennt man Heuristiken. Wenn man Heuristiken ausprobiert, wäre es gut, den Erfolg zu messen. Sie haben immer wieder diese Heuristiken getestet: Ist eine Anweisung tautologisch und kann sie weggelassen werden. Bis am Ende der Konflikt mit den 2 Tripeln mit 7825 übrig blieb – mal einfach gesagt.
Rike Hey, das ist clever. Wie geht das genau?
Ben Das geht iterativ – bis i = 4. Zuerst setzt man für jede Variable
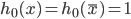
Dann wird in jedem Schritt i ein Mittelwert 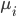 berechnet:
berechnet:
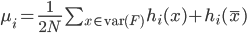
Dieses 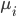 geht als Gewicht in die Formel für das nächste i ein:
geht als Gewicht in die Formel für das nächste i ein:
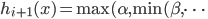
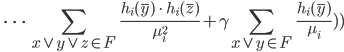
Rike Oh! Und 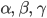 ?
?
Ben Na, sie haben
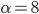
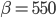
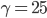
genommen. 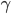 wichtet die binären Zweige oder die negative Zustände,
wichtet die binären Zweige oder die negative Zustände,  wichtet den minimalen heuristischen Wert,
wichtet den minimalen heuristischen Wert, 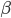 den maximalen. Und das hat funktioniert!
den maximalen. Und das hat funktioniert!
Rike Wow!
***
Übungsaufgaben
- Überprüfe die Heuristik-Bewertung in Einzelfällen.
- Überprüfe, ob die Erweiterungsregel SAT-äquivalent ist.
