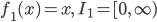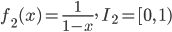Lila erzählt Max von ihren ersten Analysis-Vorlesungen im letzten Wintersemester bei Kubicki. Sie schildert, dass es am Anfang recht schwer für sie war.
Lila Ich saß in der Vorlesung, die ganze Tafel ist voll mit Formeln, und plötzlich merkte ich, dass das was mit mir selbst zu tun hat, dass es nicht nur ums Verstehen geht, sondern das das, was an der Tafel steht, mein Leben verändern kann.
Max Ehrlich? Ich hatte solche Momente eher am Ende des Studiums.
Lila Jetzt erzähle ich dir eine Geschichte, how I became excited about the lecture.
Max Du hast nicht einfach ganz brav die Tafel abgeschrieben?
Satz von Weierstraß
Lila Nein! Ich wusste ja schon von Jenny, dass die Analysis-Vorlesung die erste große Herausforderung ist. Folgen, Funktionen, Differenzieren und Integrieren – und das deutlich über unserem Abi-Niveau in Indien. Prof. Kubicki hat die Analysis-Vorlesung gehalten, das weißt du schon, he loves Functional Analysis, er kam in Turnschuhen und T-Shirt, die älteren Profs mochten ihn irgendwie nicht, wir aber umso mehr. Lively – wie heißt das deutsch?
Max Munter.
Lila Thanks, Max, also munter ging es von einer Vorlesung zur nächsten – bis zum Satz von Weierstraß:
Eine stetige Funktion nimmt auf einem abgeschlossenen, beschränkten Intervall ihr Minimum und ihr Maximum an.
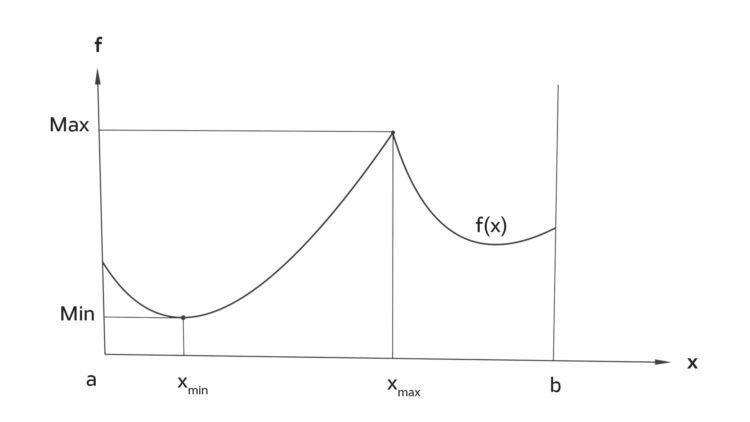 Lilas Versuche, das Gegenteil zu zeichnen
Lilas Versuche, das Gegenteil zu zeichnen
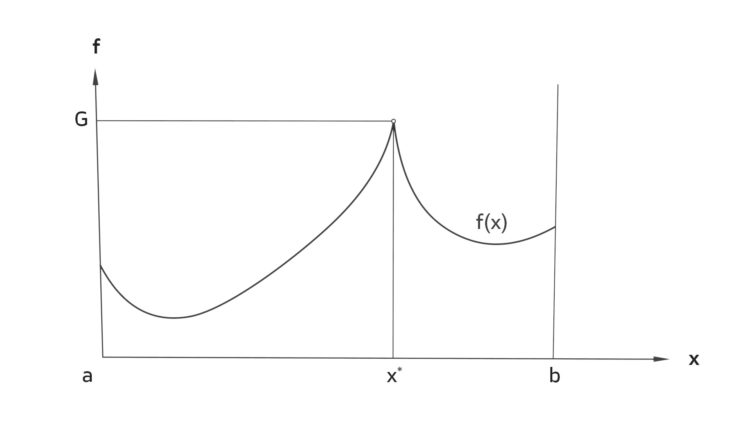
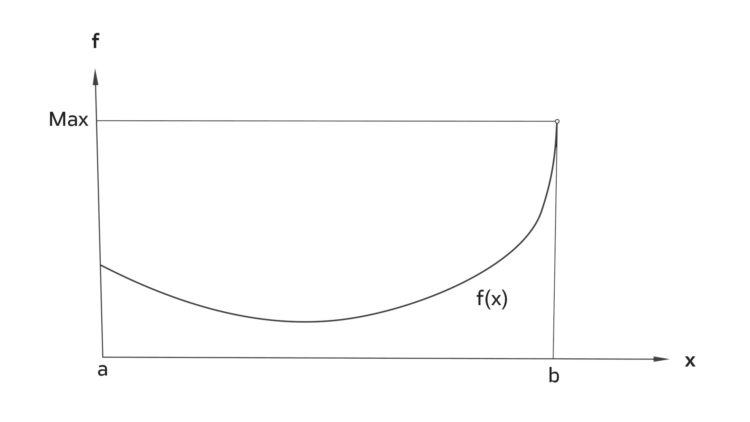
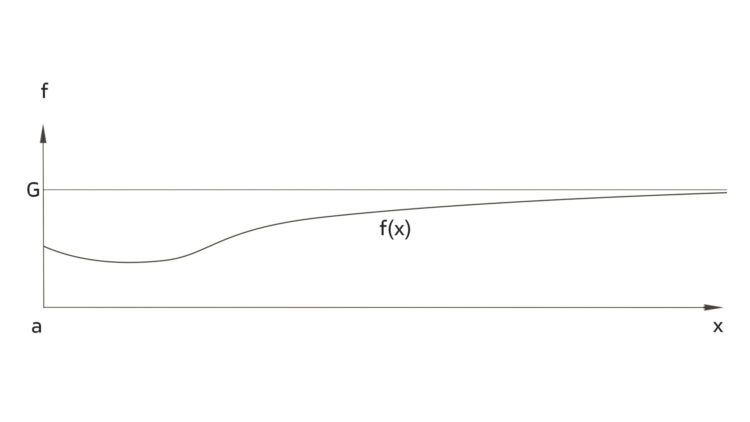
Das sollte indirekt bewiesen werden. Kubicki sagte, now we take for true that the function f ihr Maximum nicht annimmt und G die kleinste obere Schranke sei. Da habe ich versucht, das zu skizzieren und habe gemerkt, dass das nicht geht. Wenn ich eine Funktion f zeichne, die ihr Maximum auf einem abgeschlossenen, beschränkten Intervall n i c h t annimmt, dann ist f entweder nicht stetig,
das Intervall ist nicht abgeschlossen,
oder das Intervall ist nicht beschränkt. You understand.
Max Hmm ???
Kubickis Beweis
Lila Diese Annahme, die Kubicki dann geschickt zum Widerspruch geführt hat, hat er benutzt, in dem er von f dieses G abgezogen hat:
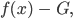
was in meiner Zeichnung an der Stelle x = xmax zu Null wird, und bei ihm ja nicht, bei ihm ist die Differenz positiv; diese Differenz hat Kubicki in den Nenner einer neuen Funktion g gesteckt:
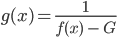
Er hat somit durch Null dividiert, because of his assumption, there is one smallest G for f mit der Eigenschaft:
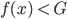
So hat er einen Widerspruch hinbekommen, wenn es dich interessiert, hat er die Formel für g nach f aufgelöst:
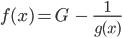
Die Funktion g ist nach seiner Voraussetzung positiv, stetig und somit beschränkt, sagen wir mal durch C:
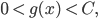
woraus dann
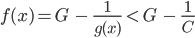
folgt. Damit hat er eine noch kleinere Schranke für f als G bekommen, 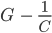 !
!
Max Hey! Indirekter Beweis! Division durch Null! Echt nur für Mathematiker!
Lilas wirtschaftsmathematisches Gegenbeispiel
Lila Genau! Das hat mich ziemlich aufgeregt. Für eine unsinnige Konstellation einen Widerspruch zu kriegen und damit den Weierstraß-Satz beweisen? Ich habe es nicht ausgehalten und mich gemeldet. Da fiel mir sogleich ein nettes Beispiel ein, da dachte ich, I'd dethrone him.
Max Haha! Was hast du gesagt?
Lila Wenn ich nämlich meinen Kontostand als stetige Funktion betrachte, dann sieht der ungefähr so aus:
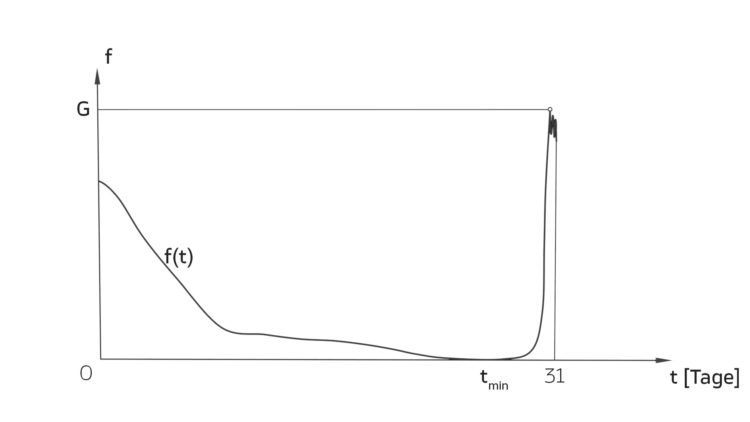
Am Monatsende bekomme ich immer Nachschub. Doch bevor das monatliche Maximum wirklich angenommen wird, wird es mit den Ausgaben der Kreditkarte verrechnet! Niemals erreiche ich das Maximum, leider aber oft das Minimum! Das wäre doch mal ein echtes Beispiel instead of this formal eyewash!
Max Und?
Lila Alle haben gelacht. Kubicki hat geantwortet, dass er nur Analysis mit boolewertigen Wahrheitswerten macht und dass die Wirtschaftsmathematik im anderen Institut wäre.
Übungsaufgaben
- Finde eine stetige Funktion f1:
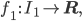
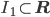 , die sich formelmäßig ausdrücken lässt und die ihr Maximum nicht auf I1 annimmt!
, die sich formelmäßig ausdrücken lässt und die ihr Maximum nicht auf I1 annimmt! - Finde eine unstetige Funktion f2:
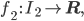
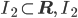 beschränkt, die sich ebenfalls formelmäßig ausdrücken lässt und die ihr Maximum nicht auf I2 annimmt!
beschränkt, die sich ebenfalls formelmäßig ausdrücken lässt und die ihr Maximum nicht auf I2 annimmt!