Rike, Charly und Ben diskutieren Wheelers Arbeit. Dessen größter Kritikpunkt beim Modell aus der DGL. 1. Ordnung ist, dass der Anfangspunkt einer Bewegung dessen Endpunkt komplett bestimmt. So wäre es doch besser, ein neues Modell zu suchen, wo Anfangs- und Endpunkt gleichberechtigt sind. Da bleibt nur eine DGL. 2. Ordnung. Vor diesem mathematischen Hintergrund probieren sie erneut ihr Roulette-Spiel. Sie haben insgesamt 100 durchnummerierte Kugeln, zufällig verteilt in 2 Urnen. Die Roulette-Maschine wirft eine Zahl von 1 – 100. Der- oder diejenige, in dessen Urne die geworfene Zahl ist, muss die Kugel mit dieser Zahl an die oder den Anderen abgeben.
Egal, mit welchem Überschuss (Surplus-Wert 
, das ist die Abweichung von 50) einer oder eine von ihnen startet, sie landen nach einiger Zeit nahe 
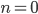. Ben simuliert das Schritt für Schritt, indem er eine Zufallszahl berechnet und die Urnen als Listen organisiert. Nach einiger Zeit bemerken Alle, dass es so eine Art Gleichgewicht um 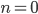herum gibt. Im zeitlichen Verlauf stellen sich Schwankungen um Null ein. Charly meint, dass das Roulette-Spiel wie ein Federschwinger funktioniert. Aber welche Amplitude und welche Frequenz hat er?
Rike Charly, das ist eine tolle Idee.
Federschwinger-DGL
Charly Ja, klar! Zu einem Federschwinger ohne Reibung gibt es die DGL:
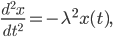
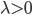
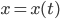ist die Auslenkung vom Ruhepunkt in Abhängigkeit von der Zeit 
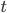. Dann haben wir 2 linear unabhängige Lösungen:
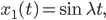
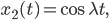
Rike Wheeler wollte unbedingt ein Randwertproblem für das Urnenspiel aufstellen, wenn wir das auch machen, hätten wir:
Randbedingungen
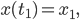
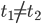. Bei unseren Urnen mit insgesamt 100 Kugeln wären nur Randwerte, die nicht größer als 100 oder nicht kleiner als -100 sind, sinnvoll:
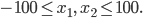
Charly Okay, und weiter?
Ansatz
Rike Wir machen den Ansatz
setzen das in die Randbedingungen ein und kriegen 2 lineare Gleichungen für die Konstanten:
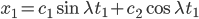
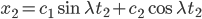
Bens Randbedingungen
Ben Ja, rechnet ihr Beiden mal. Ich arbeite mit einem Zufallsgenerator und simuliere das Spiel. Lasst uns doch mal bei dem Gleichgewicht starten, also
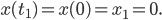
Rike Okay! Ben, was kriegst du denn nach – sagen wir mal – 2000 Würfen raus?
Ben Warte, ich muss nur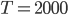 
eingeben, ja, hier, ich kriege
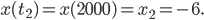
Rikes Determinante
Rike Na schön, dann haben wir ja ein paar plausible Randbedingungen. Dann rechne ich die Determinante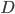 
für das lineare Gleichungssystem aus:
Charly Additionstheorem!
Rike Okay!
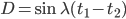
Hmm!
Charly Hey, das Randwertproblem ist nicht immer eindeutig lösbar! Für
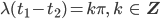
wird unsere Determinante Null! Wie ist das bei uns konkret?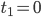 
? Dann bleibt
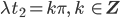
als Bedingung für eine Singularität. Ben, wie schwingt denn dein „Spiel“?
Bens Schwingung
Ben Hmm, schwer zu sagen, ich versuche mal, eine Art Schwingung
hineinzulegen, hier, für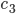 
nehme ich den Mittelwert meiner Würfe , das ist, hmm, Moment, muss ich noch ausrechnen,
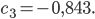
Also, meine Frequenz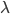 
ist:
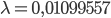
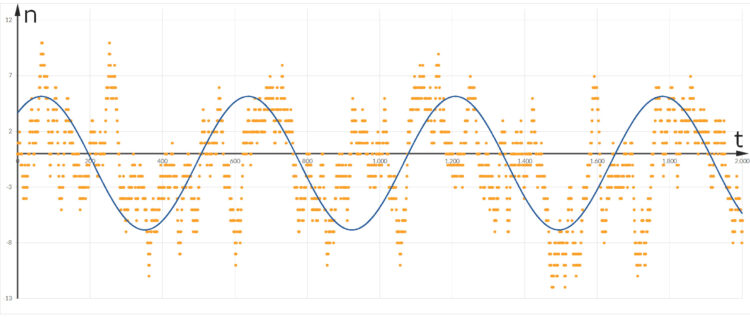
Rikes Lösung
Rike Okay, ich nehme mal dein Lambda. Dann ist
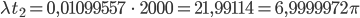
Hey, das kann nicht wahr sein! Es ist fast das 7-Fache von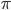 
. Was passiert, wenn ich Bens Frequenz benutze für die Lösung des Pendels? Warte, ich zeichne das mal!
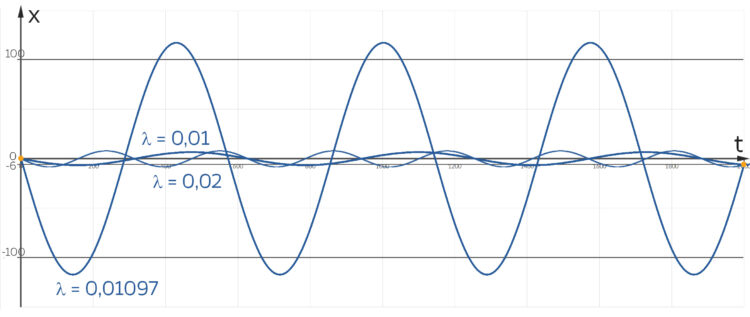
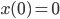und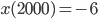 
und verschiedenen Lambdas.
Oh, Mann, für
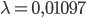
wird die Amplitude schon größer als 100, für Lambda noch näher an Bens Wert wird die Pendellösung singulär, ich kann sie nicht mehr zeichnen, die Amplituden werden riesig: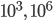 
usw.! Ausgerechnet bei den interessanten Frequenzen funktioniert das Randwertproblem nicht! Da stimmt doch was nicht!
Charly Tja, unser Federschwinger stößt an seine Montierung, fällt runter, schlägt ein Loch in den Boden... Wie haben viel mehr Kugeln als am Anfang – vielleicht 1 000, 1 Million oder noch mehr... – hey Rike, ist das die Kraft der Asymmetrie der Zeit?
Alle lachen.
***
Übungsaufgabe
Was stimmt nicht?
Lösung
Das Spiel ist nicht deterministisch. Es muss mit statistischen Methoden behandelt werden. Siehe nächster Beitrag Roulette und Zufall.