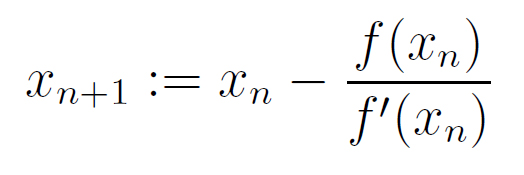Rike hat sich nach dem Abendessen mit dem Newton-Verfahren und seiner Implementierung auf einem wissenschaftlichen Taschenrechner beschäftigt. Sie hat das allerbeste Skipisten-Beispiel überprüft und andere Beispiele untersucht. Schließlich ist sie dann sehr spät nachts zu Charly ins Bett gekrochen. Dann hat sie (wieder einmal) schlecht geträumt. Beim Frühstück erzählt sie Charly ihren Traum.
Rikes Begegnung mit Newton
Rike Ich habe letzte Nacht Newton bei einer Hütte an deiner alpinen Trainingsstrecke getroffen.
Charly Aha, Newton!
Rike Jawoll, ich habe ihn erkannt und angesprochen. Zuerst wollte er gar nicht mit mir sprechen. Doch dann wollte er, dass ich ihm helfe. Er hat den Schlüssel für die Hütte gesucht. Ich glaube, er wollte astronomische Untersuchungen machen. Die Hütte hatte nämlich eine Kuppel.
Charly Und?
Rike Ich habe den Schlüssel besorgt, Schnee rund ums Haus geschoben, sodass die Tür jetzt aufging, die Heizung eingeschaltet, Kaffee gekocht usw.
Charly Haha, wie eine Praktikantin! Und Newton?
Rike Ja, ich habe mich wie eine Praktikantin gefühlt. Newton hatte sehr schlechte Laune. Wir mussten auf die Dunkelheit warten, er hat sich die Geräte angesehen und sich über die neue Technik gewundert. Da habe ich ihm von meinen Untersuchungen zum Newton-Verfahren erzählt. Vor allen Dingen habe ich ihm erzählt, dass sein Verfahren zur Bestimmung einer Nullstelle eines Polynoms jetzt in Rechnern für die Schule implementiert ist. Man braucht nur die Gleichung einzugeben, einen Startwert festzulegen und auf SOLVE zu drücken. Das Verfahren funktioniert jetzt auch für andere Funktionen f(x), differenzierbare natürlich. Voraussetzung ist, dass für die Startwerte x0 die 1. Ableitung der Funktion nicht verschwindet:
f' '(x0) ≠ 0.
Da wurde er sehr wütend: Er wurde nicht gefragt, andere verdienen damit Geld. Ich habe ihm auch noch erzählt, dass sein Verfahren manchmal nur Newton-Verfahren heißt und es irgendetwas anderes macht, sogar Lösungen findet, die mathematisch nicht plausibel sind. Da wurde er noch wütender, er wollte es genauer wissen, meinte, ich hätte ja gar keine Ahnung, die 1. Ableitung soll ungleich Null sein? Ich spinne jawohl, mit solchen wie mir gibt er sich eigentlich gar nicht ab!
Charly Ein Genie eben!
Rike Er ist immer wütender geworden, er hat herumgeschrien, er hat getobt. Er hat mich gepackt, ich habe mich gewehrt, aber er war stärker. Er hat mich in die Ecke geworfen, mich mit Füßen getreten. Ich hatte Angst. Die Dunkelheit kam, ich kauerte in der Ecke, Newton stand vor mir, meine Angst wurde immer größer – und dann bin ich aufgewacht.
Charly Ohje, Rike, was für ein furchtbarer Traum! Und das noch von einem ganz Großen! Wie geht es dir jetzt?
Rike Es ist okay.
Charly Willst du mir denn von deinen Untersuchungen zum Newton-Verfahren auf wissenschaftlichen Taschenrechnern erzählen?
Rikes Beispiel
Rike Ja, klar. Ich habe das Standardbeispiel gewählt, das ist in jedem Mathebuch und bei Wikipedia steht:
f(x) = x² – 2
Charly Aha, das kenne ich! Das hat 2 Lösungen:
x(1) = +√2,
x(2) = –√2.
1. Fall: Startwerte rechts von der positiven Wurzel
Rike Richtig. Für alle Startwerte x0:
x0 ≥ x(1) = √2
sind die Voraussetzungen des Satzes zur Konvergenz der Folge (xn) des Newton-Verfahrens
für konvexe Funktionen f(x):
f ∈ C2[a, b],
f(a) < 0,
f(b) > 0,
f konvex,
f(x0) ≥ 0,
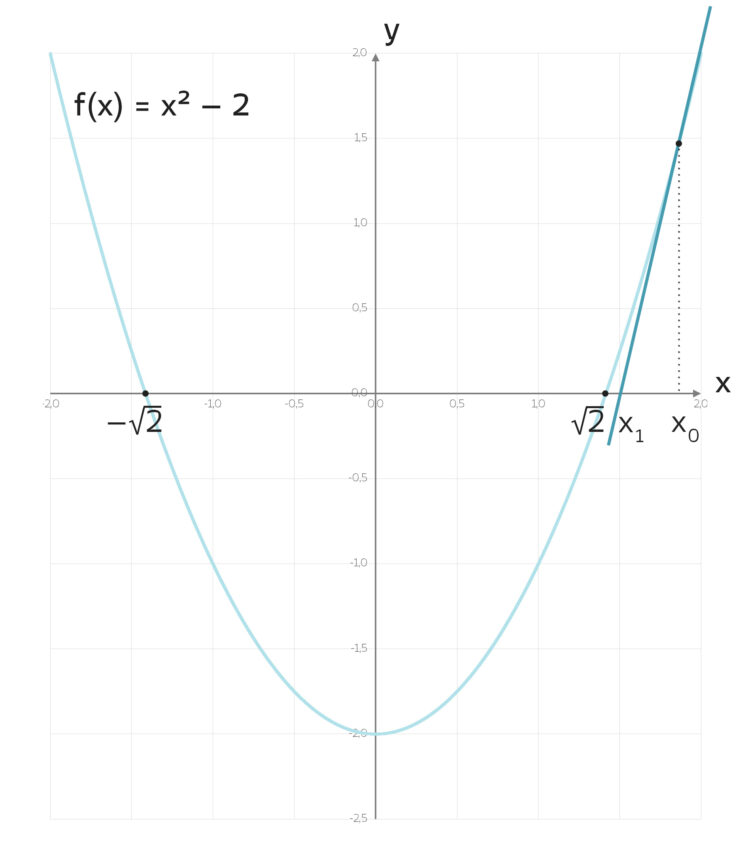
Sogar monoton fallend.
erfüllt. Weißt du noch, das haben wir an der allerbesten Skipisten-Aufgabe besprochen? Die Folge (xn) konvergiert dann monoton fallend gegen x(1).
Charly Ja, ich weiß. Alles klar. Und was ist mit den anderen Anfangswerten?
2. Fall: Positive Startwerte links von der positiven Wurzel
Rike Für alle Startwerte x0:
x0 ∈ (0, √2)
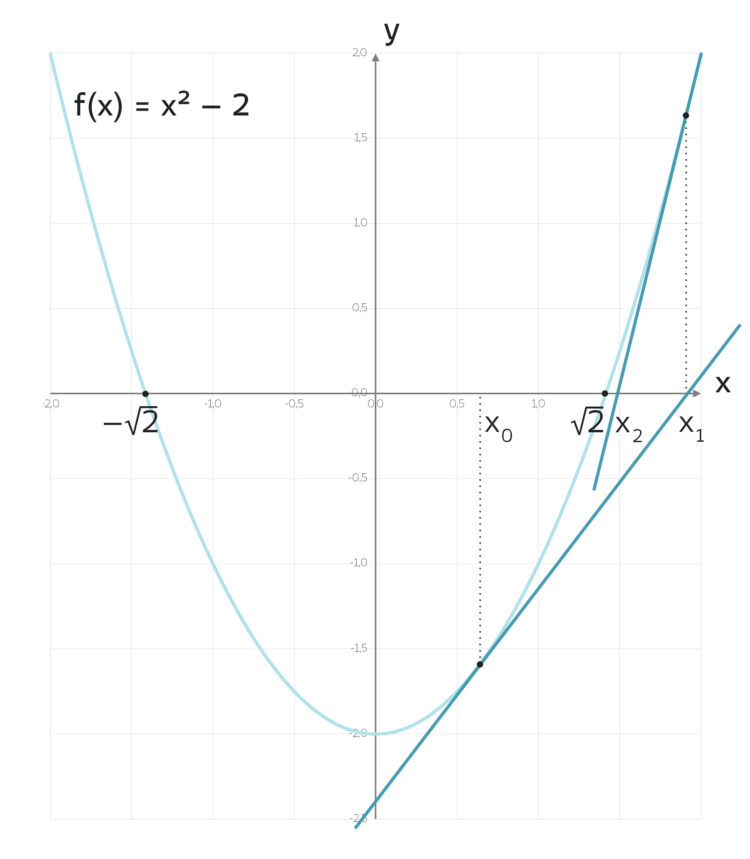
kannst du eine Tangente an die Parabel f(x) legen und der Schnittpunkt x1 dieser Tangente mit der x-Achse liegt rechts von der positiven Wurzel!
x1 > √2
Charly Okay! Und dann sind wir wieder im 1. Fall gelandet und das Verfahren konvergiert gegen √2 !
Rike Genau!
3. Fall: Startwert x0 = 0
Charly Jetzt fehlt noch der Fall x0 = 0! Das funktioniert aber nicht, da verschwindet die 1. Ableitung!
f '(0) = 0.
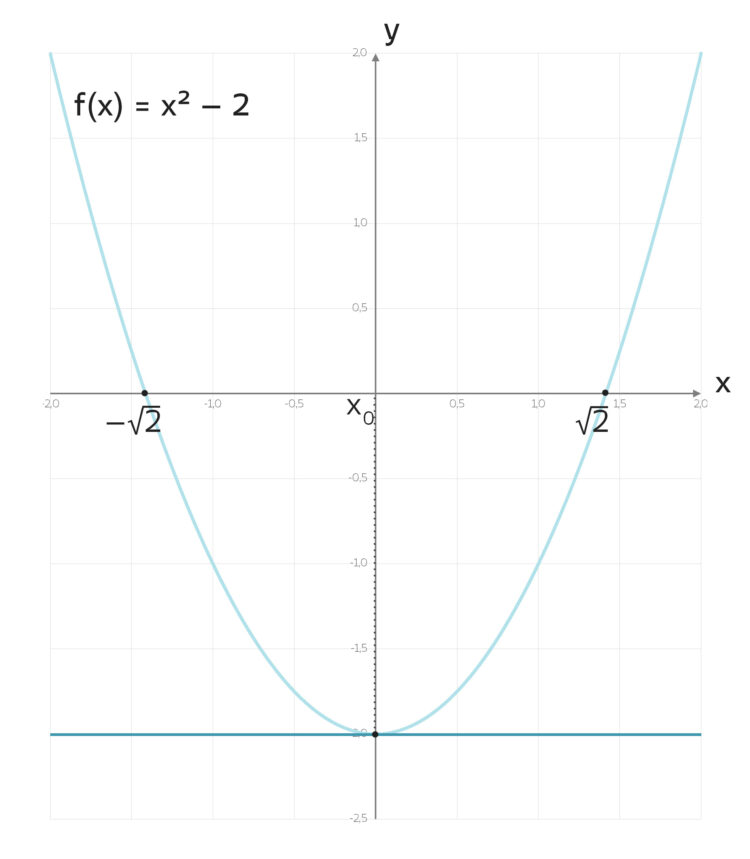
Einzugsbereiche der Nullstellen
Rike Genau. Habe ich dich nun überzeugt, dass für alle positiven Startwerte x0 die Folge (xn) gegen die positive Wurzel konvergiert?
xn → √2 für alle x0 > 0.
Charly Ja, du hast mich überzeugt.
Rike Gut. Für alle negativen Startwerte x0:
x0 < 0
kann man dasselbe machen:
xn → –√2 für alle x0 < 0.
Wir haben herausgefunden, dass das Ergebnis des Verfahrens stetig vom Startwert x0 abhängt. Man kann sogenannte Einzugsbereiche für die Nullstellen des Polynoms definieren. Die Nullstellen wirken wie Attraktoren auf die Startwerte, sieh mal, grafisch sieht das auch eindimensional toll aus:

Charly Gut. Das hast du gut gezeichnet. Wie du mir eben erklärt hast: für die positiven Startwerte gehen die Folgen nach √2, für die negativen nach –√2. Bei Null ist der Scheidepunkt.
Konvergenz des Newton-Verfahrens mittels CASIO
Rike Genau! Genau das habe ich nun mit dem CASIO getestet – also mit dem fx-991DE X-Emulator. Im Manual steht, dass das SOLVE-Tool das Newton-Verfahren benutzt.
Charly Stimmt. Hast du etwa nicht dasselbe rausbekommen?
Rike Bei den meisten Startwerten x0 klappt das gut. Aber weißt du, was beim Startwert
x0 = 0
herausgekommen ist?

Charly Da müsste eine Fehlermeldung erscheinen! Schließlich kann dieser CASIO sehr wohl differenzieren und sehr wohl die Ableitung an der Stelle x = 0 ausrechnen!
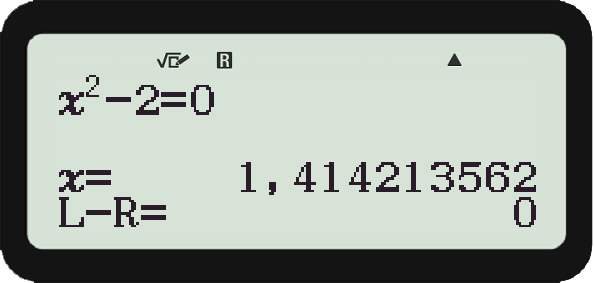
Rike Nö! Der CASIO hat irgendwas anderes gemacht!
Charly Das kann nicht sein! Das muss ich mir ansehen!
Rike Klar, tu das. Dann habe ich negative Startwerte x0 getestet, z.B.
x0 = –0.001:
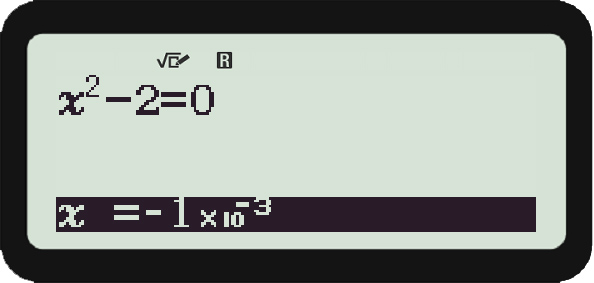
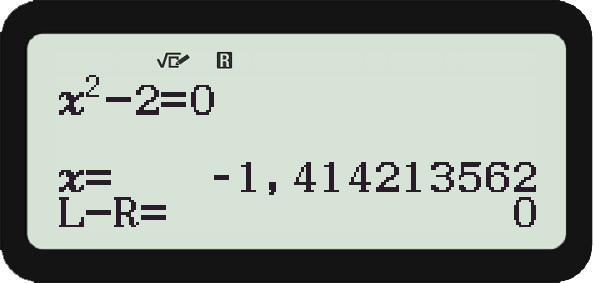
Ich habe das korrekte Ergebnis
x = –1.414213562
erhalten.
Charly Soweit so gut.
Rike Dann habe ich noch verschiedene Werte probiert, um die Stelle zu finden, wo sich die Einzugsbereiche der Attraktoren trennen. Ich habe für den kleinsten Startwert x0:
x0 = –0.0004:
gefunden, für den die Folge (xn) nach √2 strebt.
Charly Das kann nicht sein! Ein negativer Startwert führt zu einer positiven Lösung! Das muss ich mir ansehen!
Rike Hier!
Rikes kritischer Startwert
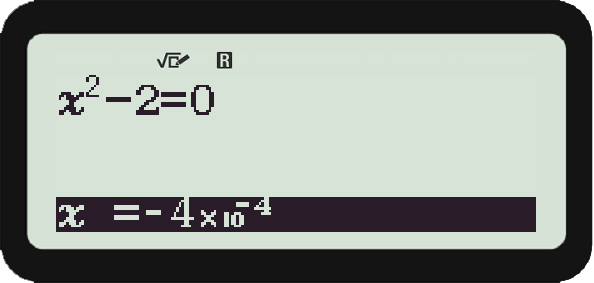

Rike Jetzt bist du ziemlich wütend, Charly! Wollen wir mal eine Pause machen?
Charly Nein, mach weiter!
Rike So habe ich durch diskrete Versuche die Einzugsbereiche der Nullstellen getestet. Sie scheiden sich bei
x0 = –0.0004.

Charly O nein, alles ist verschoben! Vielleicht das Sekanten-Verfahren?
Chaos im Nahbereich des kritischen Wertes
Rike Das habe ich mir auch gedacht und überprüft. Aber schließlich habe ich noch einige Werte zwischen –0.0004 und 0 überprüft. Ich habe gefunden, dass manche Werte zur positiven Nullstelle konvergieren und manche zur negativen – unabhängig von ihrer Lage zueinander! Die stetige Abhängigkeit des Ergebnisses von den Startwerten konnte ich nicht verifizieren! Hier sind meine Ergebnisse:
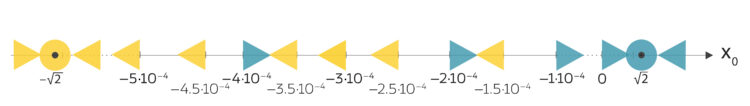
Charly Jetzt bist du aber wütend!
Rike Stimmt, ich bin wütend. Ich hätte gern gewusst, welches Verfahren nun wirklich im CASIO benutzt wird. Ich habe es nicht herausgefunden.
Charly Du hast schon sehr viel herausgefunden. Toll, Rike! Für die Schule und das Abi, wo wir diesen Rechner benutzen, ist das weniger toll! Wir wissen gar nicht, wie der CASIO rechnet! Ich bin gespannt, was meine Kollegen und Schüler dazu sagen.
***
Übungsaufgaben
Teste selbst Näherungen der Wurzeln von
x² – 2 = 0
und versuche, Rikes Ergebnisse zu verifizieren!