Max und Lila sind in Berlin zusammen – an einem dieser Abende, wo sie lieber ins Kino oder zur Party gegangen wären. Außerdem ist Winter, ein eisiger Wind weht. Lila hat ihr 3. Semester an einer Berliner Uni fast geschafft. Sie hat die meisten Vorlesungen an ihrem Rechner verfolgt. Die Vorlesung über gewöhnliche Differenzialgleichungen hat ihr von Anfang an Spaß gemacht. Sie hatte eine neue junge Dozentin: Anna Krotofil. Die hat die Vorlesung mit ein paar motivierenden Beispielen gestartet und das Interessanteste war ein System von DGLn über die Ausbreitung ansteckender Krankheiten, das Kermack-McKendrick-Modell. Davon erzählt sie heute Abend Max.
Lila Das Modell geht so: Man überlegt, wie sich die Anzahl von Infizierten 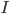 , von Susceptibles
, von Susceptibles 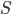 – wie heißt das Deutsch? …
– wie heißt das Deutsch? …
Max Susceptibles - das sind die Anfälligen, in den Medien heißen die heute die Gefährdeten.
Lila Also gut, die Gefährdeten 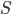 , das sind die, die an der ansteckenden Krankheit erkranken können und die Removed
, das sind die, die an der ansteckenden Krankheit erkranken können und die Removed 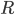 – wie sagt ihr dazu?
– wie sagt ihr dazu?
Max Meinst du die Gestorbenen?
Lila Ja! Also die Gestorbenen 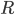 . Du überlegst, wie sich die Anzahl von
. Du überlegst, wie sich die Anzahl von 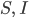 und
und 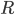 ändert. Wenn die Gefährdeten erkranken, werden sie Infizierte, je mehr es von beiden gibt, umso stärker verringert sich die Anzahl
ändert. Wenn die Gefährdeten erkranken, werden sie Infizierte, je mehr es von beiden gibt, umso stärker verringert sich die Anzahl 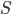 , das heißt
, das heißt
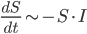
Den Proportionalitätsfaktor haben die Erfinder 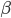 benannt, er steht für die Ansteckungsrate, also
benannt, er steht für die Ansteckungsrate, also
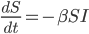
Und genauso ist es mit den Infizierten, dort ist der Zuwachs 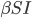 und außerdem sterben einige Infizierte mit der Sterberate
und außerdem sterben einige Infizierte mit der Sterberate 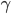
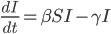
Mit derselben Rate 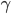 nimmt die Anzahl von
nimmt die Anzahl von 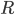 zu:
zu:
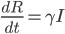
Das Kermack-McKendrik-Modell über die Ausbreitung einer ansteckenden Krankheit
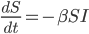
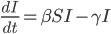
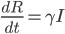
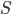 … ist die Anzahl der Anfälligen (Susceptibles), also solche, die die Krankheit noch nicht hatten und nicht immun sind
… ist die Anzahl der Anfälligen (Susceptibles), also solche, die die Krankheit noch nicht hatten und nicht immun sind
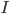 … ist die Anzahl der Infizierten
… ist die Anzahl der Infizierten
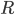 … ist die Anzahl der übrigen (Removed), also solche, die tot, isoliert oder immun sind
… ist die Anzahl der übrigen (Removed), also solche, die tot, isoliert oder immun sind
 … Ansteck- bzw. Sterberate
… Ansteck- bzw. Sterberate
Max Wow!
Lila Ja, so hat es Anna Krotofil dargestellt.
Gleichgewichtszustände
Es sind nichtlineare DGLn und eigentlich kaum zu lösen, aber sie sind eins der ersten Modelle für die Ausbreitung ansteckender Krankheiten – von 1927! Obwohl ich nicht ganz das Mathetalent bin, konnte die Herleitung von Anna Krotofil verstehen.
Dann haben wir die DGLn noch mal angeschaut und herausgefunden, dass
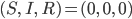
eine Lösung ist.
Max Ja, toll! Das ist die Lösung, die alle anstreben! Keine Epidemie!
Lila Ja, richtig. Außerdem sind
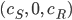
weitere zeitlich konstante Lösungen.
Max Okay, wenn es keine Infizierten gibt, ändert sich nichts.
Lila Richtig. Sinnvolle Anfangswerte sind
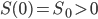
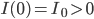
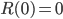
Max Okay, verstehe.
Qualitative Eigenschaften von Lösungen nichtlinearer DGLn
Lila Außerdem haben wir überlegt: Wenn es eine Lösung dieses Anfangswertproblems gäbe und 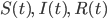 wären immer nicht negativ, genauer:
wären immer nicht negativ, genauer:
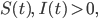
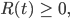
dann wäre für diese Lösungen der DGLn
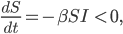
das heißt die Anzahl der Gefährdeten nimmt immerzu ab,
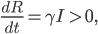
die Anzahl der Gestorbenen nimmt dauernd zu. Aber bei 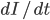 können wir Wachstum oder auch ein Abnahme haben, je nachdem ob:
können wir Wachstum oder auch ein Abnahme haben, je nachdem ob:
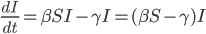
positiv, negativ oder Null ist. Wenn
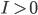
ist, dann bleibt nur das Vorzeichen von
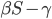
zu untersuchen.
Szenario 1
Krotofil hat gesagt, eine Epidemie erkennt man daran, dass die Anzahl der Infizierten bis zu einer Zeit 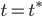 anwächst und danach wieder abfällt. Wenn ich also schon bei den Anfangsbedingungen
anwächst und danach wieder abfällt. Wenn ich also schon bei den Anfangsbedingungen
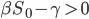
wähle, dann wächst 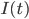 , ich weiß nur nicht, ob die Anzahl auch mal wieder fällt.
, ich weiß nur nicht, ob die Anzahl auch mal wieder fällt.
Szenario 2
Wenn ich
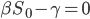
wähle, dann ist
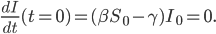
Weil 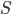 aber immer fallend ist, wird sofort
aber immer fallend ist, wird sofort
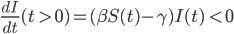
und es kommt nicht zu einer Epidemie.
Szenario 3
Als letztes bleibt nur,
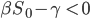
zu wählen, dann fällt 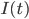 sofort und es gibt ebenfalls keine Epidemie.
sofort und es gibt ebenfalls keine Epidemie.
Max Na gut! Aber ihr wisst ja noch gar nicht, ob es überhaupt zeitlich veränderliche Lösungen gibt!
Lilas numerische Lösung
Lila Stimmt! Dazu kommen wir erst später. Aber ich habe einfach mein Notebook herausgenommen und wollte das überprüfen. Ich hatte ja schon einmal mit Jenny numerisch die Gleichungen für das Pendel mit der Methode von Runge-Kutta implementiert …
Max Was hast Du?
Lila …. Ich habe das alte Programm ein bisschen angepasst und dann habe ich mir Berlin, Kalkutta oder eine Insel vorgestellt, habe mir Ansteck- und Todesraten überlegt und habe mit nur einem Infizierten ausprobiert, ob es mit diesem Modell zu einer Epidemie kommen kann!
Max Und was hast Du herausgefunden?
Lila Ich bin die 3 Szenarien mit nur einem Infizierten
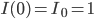
durchgegangen und haben die Kurven berechnet, hier schau mal:
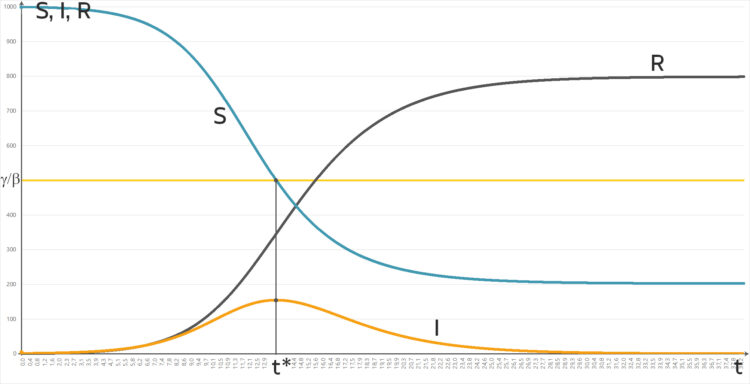
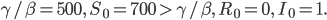 Das Maximum der Infizierten tritt bei
Das Maximum der Infizierten tritt bei 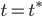 ein, genau dann, wenn
ein, genau dann, wenn 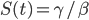
Max Bei nur einem Infizierten sterben 800 Leute?
Lila Ja! Und 200 überleben. Außerdem hat meine numerische Lösung das Epidemie-Kriterium
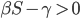
bestätigt. Als
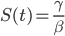
wurde, war gerade der Höhepunkt der Infektionen erreicht, bei 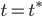 .
.
Max Aha! Lila, du bist ja unglaublich!
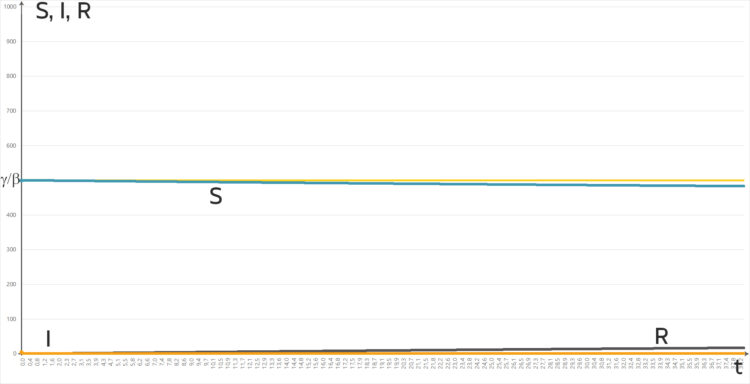
 Keine Epidemie.
Keine Epidemie.
Lila Beim 2. Szenario fiel die Zahl der Gefährdeten sehr langsam, und die Zahl der Infizierten stieg nicht an.
Max Sehr gut!
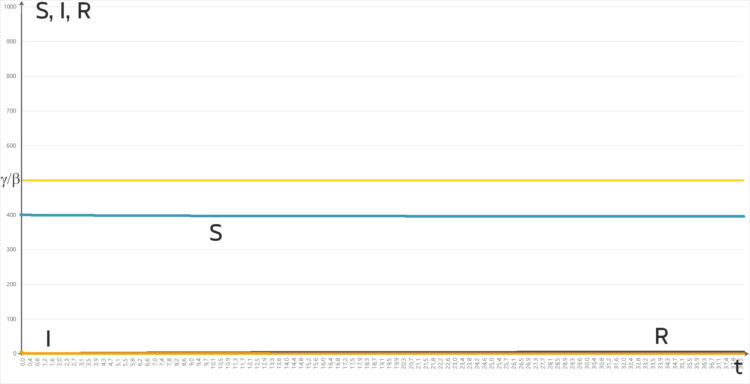
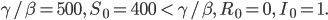 Keine Epidemie.
Keine Epidemie.
Lila Und beim 3. Szenario war es ebenso.
Max Aha! Dann hast du herausgefunden, wenn die Anfangszahl der Gefährdeten 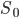 groß genug ist:
groß genug ist:
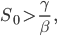
dann kommt es zu einer Epidemie.
Lila Ja, das ist die einzige Bedingung.
***
Übungsaufgabe
Überprüfe, dass die Summe Aller konstant bleibt: