Rike, Charly und Ben diskutieren immer noch das 2-Urnen-Spiel. Ben ist aufgefallen, dass sie bei ihren Betrachtungen zur Zufallsverteilung der Überschusswerte die zeitliche Entwicklung des Spiels ganz außer Acht gelassen haben.
Brownsche Bewegung
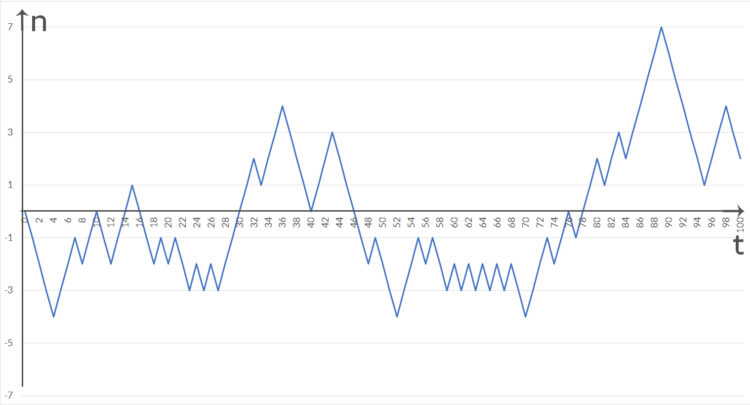
Ben Diese Funktionsverläufe der Surplus-Werte kommen mir merkwürdig bekannt vor.
Charly Na klar! Haha! Das sehe ich jeden Tag!
Ben Ja, klar! Es ist so präsent, dass ich es verdränge.
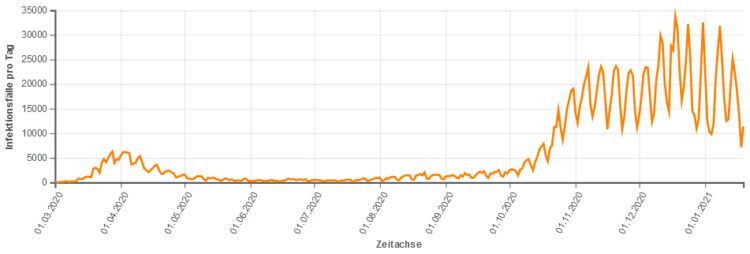
Charly Ölpreise, Infektionsgeschehen ...
Ben Aber was für ein Modell steckt dahinter?
Charly Das ist die brownsche Bewegung! Die beschreibt die zufällige Geschwindigkeit eines Teilchens in einem Volumen oder auch die Preisentwicklung oder die Anzahl der Corona-Infizierten und vielleicht die Surplus-Werte in einer von den beiden Urnen.
Ben Aha! Die brownsche Bewegung?! Ein Random Walk? Wie können wir das prüfen?
Charly Warte, hier: Das allgemein anerkannte mathematische Modell ist der Wienerprozess. Der wird seit 100 Jahren untersucht und ist ein schönes Modell, nicht zu einfach, ja, schon anspruchsvoll, Norbert Wiener hat das vorangetrieben. Jetzt ist es ein aktuelles Forschungsthema.
Ben Gut.
Wienerprozess für kleine Fallzahlen
Charly Wir setzen die zeitliche Entwicklung des Surplus-Wertes 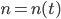 als Wienerprozess an:
als Wienerprozess an:
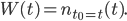
Damit ist die Liste der Surpluswerte aus deinen Zufallszahlen ab dem Zeitpunkt 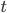 gemeint. Damit es wirklich ein Wienerprozess ist, musst du unter anderem schauen, ob die Differenz
gemeint. Damit es wirklich ein Wienerprozess ist, musst du unter anderem schauen, ob die Differenz
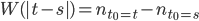
für alle 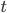 und
und 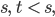 unabhängig, normalverteilt mit
unabhängig, normalverteilt mit 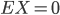 und einer Standardabweichung
und einer Standardabweichung 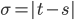 ist. Dann hätten wir ein schönes physikalisches und ökonomisches Analogon, außerdem könnten wir dann ein paar Eigenschaften des Prozesses vorhersagen.
ist. Dann hätten wir ein schönes physikalisches und ökonomisches Analogon, außerdem könnten wir dann ein paar Eigenschaften des Prozesses vorhersagen.
Ben Okay. Ich berechne das mal. Können wir mal für die zeitliche Differenz eine neue Variable nehmen – zum Beispiel
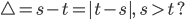
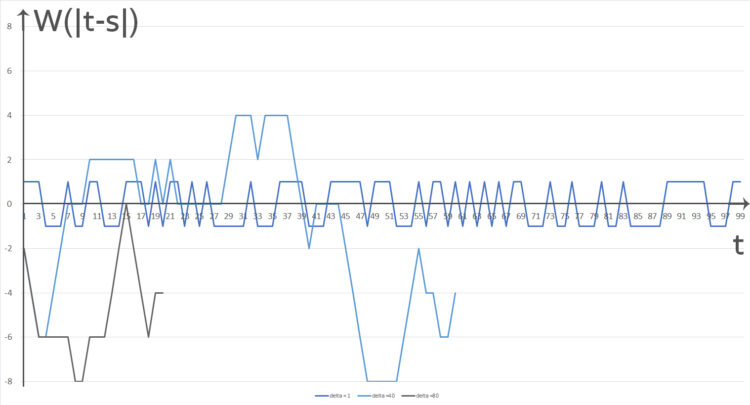
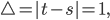 für
für 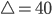 und für
und für 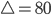 bei 100 Würfen.
bei 100 Würfen.Charly Na klar. Sag mal Ben, diese Differenz  hat so eine seltsame Gestalt: Bei nur einem Zeitschritt, also bei
hat so eine seltsame Gestalt: Bei nur einem Zeitschritt, also bei 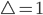 kriegst du nur die Zahlen 1 und -1. Hmm, das muss am Urnenspiel selbst liegen. Warte mal, wenn eine Kugel aus einer Urne herausgenommen wird, dann ist Änderung des Surplus-Wertes natürlich -1, wenn sie hinzukommt ist sie +1, wenn sie drin ist, wird sie 0. Lass uns nun die zeitliche Änderung
kriegst du nur die Zahlen 1 und -1. Hmm, das muss am Urnenspiel selbst liegen. Warte mal, wenn eine Kugel aus einer Urne herausgenommen wird, dann ist Änderung des Surplus-Wertes natürlich -1, wenn sie hinzukommt ist sie +1, wenn sie drin ist, wird sie 0. Lass uns nun die zeitliche Änderung 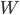 berechnen. Irgendwie wird das jetzt kompliziert!
berechnen. Irgendwie wird das jetzt kompliziert!
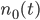 | 0 | -1 | 0 | 1 | 0 | 1 | 2 | 1 | 2 | 3 | … |
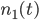 | -1 | 0 | 1 | 0 | 1 | 2 | 1 | 2 | 3 | 4 | … |
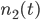 | 0 | 1 | 0 | 1 | 2 | 1 | 2 | 3 | 4 | 5 | … |
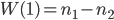 | -1 | -1 | 1 | -1 | -1 | 1 | -1 | -1 | -1 | -1 | … |
Surpluswerte aus Bens Zufallsgenerator, um einen Zeitschritt nach links verschoben, um 2 Zeitschritte, Differenz 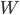 | |||||||||||
Aha! Richtig, 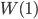 hat nur die Werte
hat nur die Werte 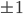 .
. 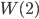 hat nur die Werte -2, 0, 2, usw.
hat nur die Werte -2, 0, 2, usw.
Ben Stimmt. Dann wird dieses 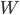 aber kaum eine Chance für die Normalverteilung mit Erwartungswert Null haben.
aber kaum eine Chance für die Normalverteilung mit Erwartungswert Null haben.
Charly Hmm, das haben wir ein Problem.
Chi-Quadrat-Test
Ben Ich teste das mit Rikes Chi-Quadrat-Test.
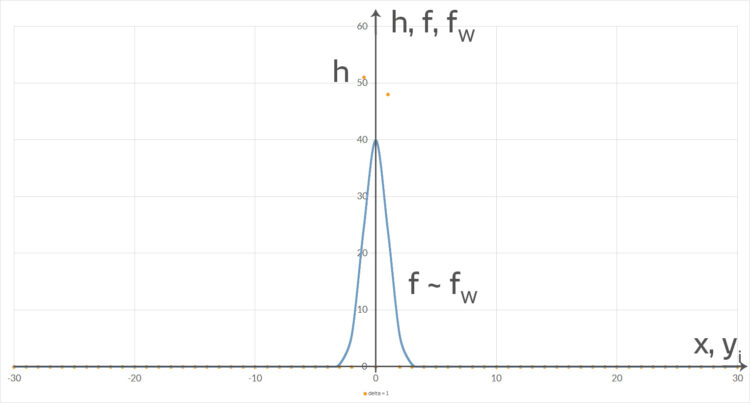
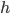 der Zahlen
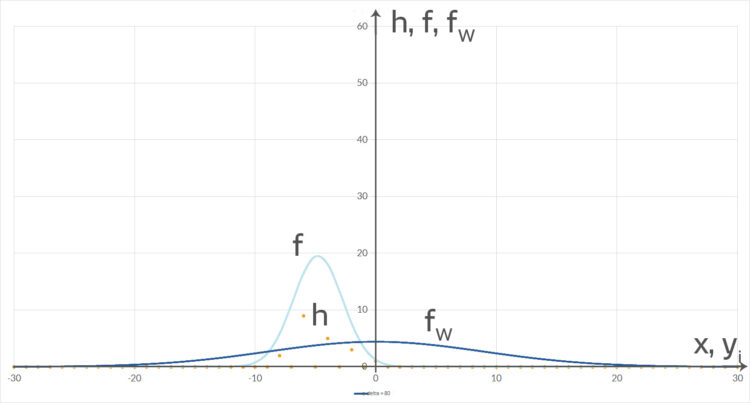
der Zahlen 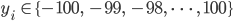 für
für 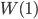 . In Orange für die Häufigkeitswerte für Bens Roulette-Spiel. In Hell- bzw. Dunkelblau (übereinanderliegend) die Normalverteilung
. In Orange für die Häufigkeitswerte für Bens Roulette-Spiel. In Hell- bzw. Dunkelblau (übereinanderliegend) die Normalverteilung 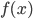 zum Spiel bzw. die Normalverteilung
zum Spiel bzw. die Normalverteilung 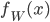 mit
mit 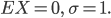 Der Chi-Quadrat-Test ist 95 % erfüllt. N = 100.
Der Chi-Quadrat-Test ist 95 % erfüllt. N = 100.
 mit
mit 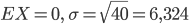 für
für 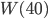 . Der Chi-Quadrat-Test ist erfüllt.
. Der Chi-Quadrat-Test ist erfüllt.
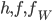 mit
mit 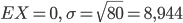 für
für 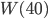 . Der Chi-Quadrat-Test ist erfüllt.
. Der Chi-Quadrat-Test ist erfüllt.
Charly Naja, mit größerer Zeitdifferenz ∆ gehen die Erwartungswerte und die Standardabweichung immer mehr auseinander. Wenn du die Differenz von 80 nimmst, hast du nur noch 20 Würfe zu analysieren. Ist das nicht etwas zu wenig?
Wienerprozess für große Fallzahlen
Ben Okay. Ich kann natürlich auch viel länger testen. Sind 2000 Würfe okay?
Charly Ja, das beweist mathematisch zwar gar nichts, aber wir kriegen ein Gefühl.
Ben Gut. Also hier, wenn wir die Differenz zwischen 2 Würfen betrachten…
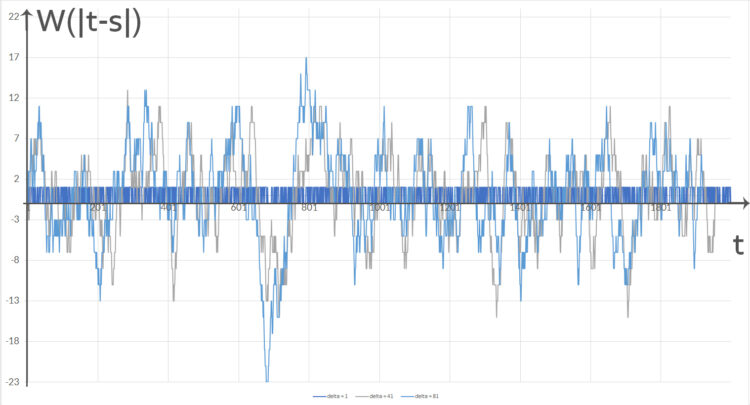
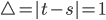 , für
, für 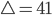 und für
und für 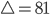 bei 2000 Würfen.
bei 2000 Würfen.… haben wir für 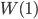 wieder nur die Werte +1 oder -1. Die Null ist nicht dabei. Die Häufigkeiten der 1 oder -1 liegen bei 1000. Das ergibt einfach keine Normalverteilung. Die einzelnen Punkte sind zu weit von der Gaußkurve entfernt. Der Chi-Quadrat-Test fällt negativ aus.
wieder nur die Werte +1 oder -1. Die Null ist nicht dabei. Die Häufigkeiten der 1 oder -1 liegen bei 1000. Das ergibt einfach keine Normalverteilung. Die einzelnen Punkte sind zu weit von der Gaußkurve entfernt. Der Chi-Quadrat-Test fällt negativ aus.
Ben Aha! Welche Wahrscheinlichkeit hast du genommen? 95 %?
Charly Ja! Aber auch bei 50 % ist er nicht erfüllt.
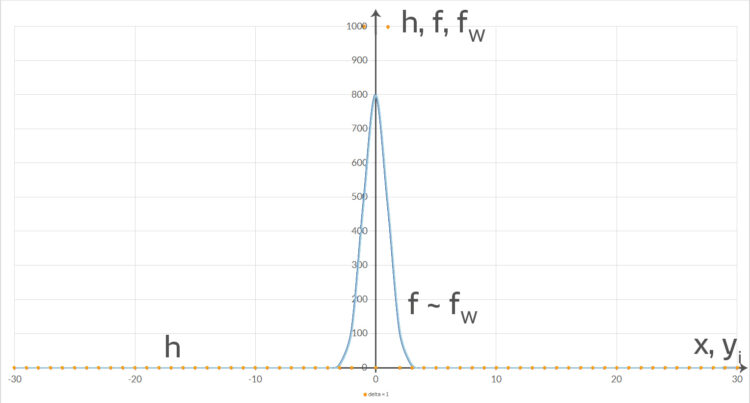
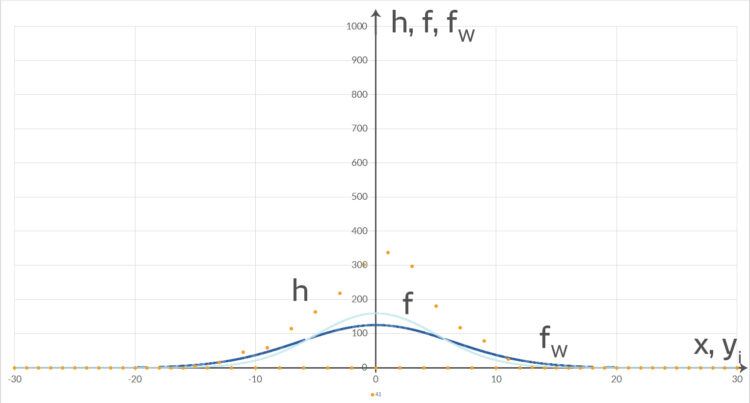
 der Zahlen
der Zahlen 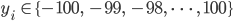 für
für 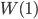 in Orange, in Hell- bzw. Dunkelblau die Normalverteilung
in Orange, in Hell- bzw. Dunkelblau die Normalverteilung 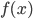 des Roulette-Spiels bzw. die Normalverteilung
des Roulette-Spiels bzw. die Normalverteilung 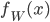 mit
mit 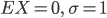 . Hier liegen die beiden Kurven übereinander. Der Chi-Quadrat-Test ist bei 95 % nicht erfüllt. N = 2000.
. Hier liegen die beiden Kurven übereinander. Der Chi-Quadrat-Test ist bei 95 % nicht erfüllt. N = 2000.
 mit
mit 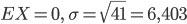 für
für 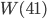 . Der Chi-Quadrat-Test ist nicht erfüllt.
. Der Chi-Quadrat-Test ist nicht erfüllt.
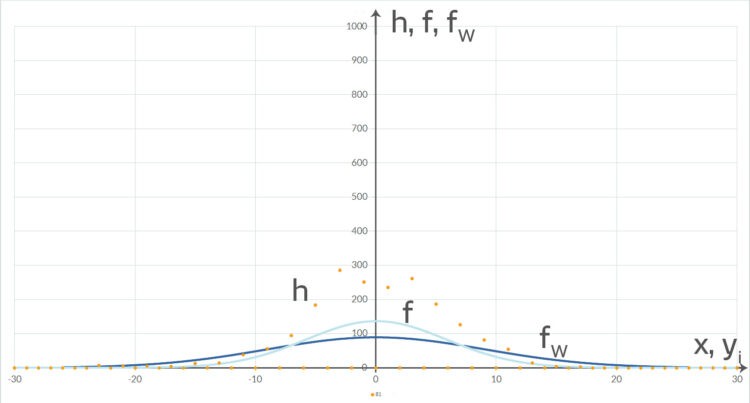
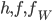 mit
mit 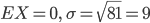 für
für 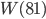 . Der Chi-Quadrat-Test ist nicht erfüllt.
. Der Chi-Quadrat-Test ist nicht erfüllt.
Fazit
Ben Na, schade, auch wenn wir mit unseren Anforderungen noch etwas heruntergehen, ist dieser Wienerprozess beim 2-Urnen-Spiel kein Wienerprozess – obwohl der zeitliche Verlauf der Surplus-Werte den Eindruck machte. Es hat nichts mit zufälligen Wegen von Viren im Volumen, nichts mit den Schwankungen des Rohölpreises zu tun, Charly – shit happens!
Charly Sehr witzig! Viren! Jetzt hast du den ganzen Abend programmiert und meine Vermutung hat nicht gestimmt.
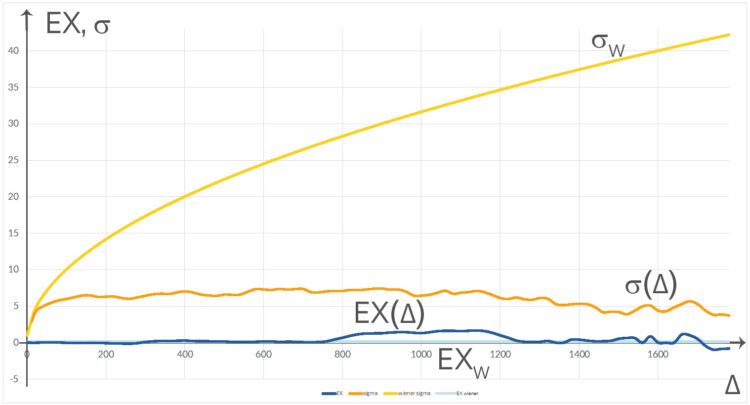
Rike Aber das ist doch nicht schlimm! Wir müssen doch nicht unsere Modelle zu den Erkenntnissen hin verbiegen! Nur um die Selbstähnlichkeit zu kriegen oder ein paar nette topologische Eigenschaften eines Random Walk zu bekommen? Diese Idee des Wienerprozesses, nämlich
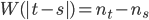
auszurechen, ist doch echt genial. Ihr Beide habt herausgefunden, dass dieses 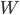 nicht normalverteilt ist, dass der Erwartungswert nahe Null bleibt und die Standardabweichung von
nicht normalverteilt ist, dass der Erwartungswert nahe Null bleibt und die Standardabweichung von 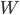 nahezu konstant bleibt. Das ist doch was!
nahezu konstant bleibt. Das ist doch was!
Charly Rike, meinst du, dass die Änderungen beim Roulette immer in der Nähe der Null bleiben und die Standardabweichungen recht klein sind und sich kaum ändern? Das ich also – niemals gewinne?!
Rike Ach, Charly!
***
Übungsaufgaben
Ermittle den zeitlichen Verlauf 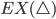 und
und 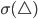 von
von 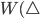 für das 2-Urnen-Spiel.
für das 2-Urnen-Spiel.
Lösung