Charly wundert sich, dass Rikes "seriöse" Lösung der IGA-Abiaufgabe ein anderes Ergebnis als die Musterlösung liefert. Rike hat ein regelmäßiges Muster, das die Anforderung von 6 Blumen pro m² erfüllt, gefunden und damit die gegebene Fläche  zwischen den Kurven
zwischen den Kurven 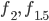 und der
und der  -Achse von knapp 30 m² ausgelegt.
-Achse von knapp 30 m² ausgelegt.
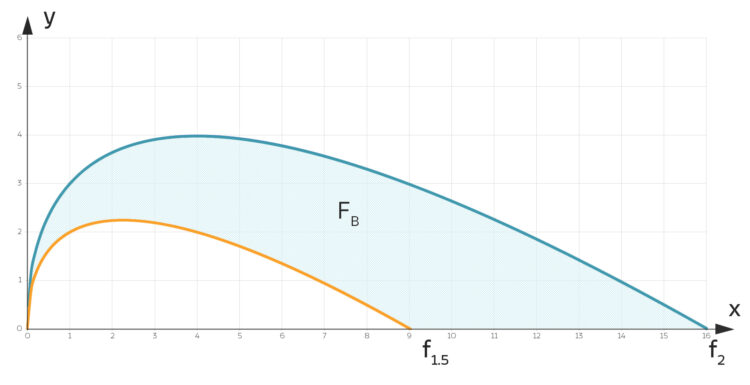
 , die mit Blumen zu belegen ist. Für die Formeln von
, die mit Blumen zu belegen ist. Für die Formeln von  und
und  siehe Beitrag Die IGA-Aufgabe.
siehe Beitrag Die IGA-Aufgabe.Bei der Musterlösung war die Fläche unabhängig von der Geometrie zu bepflanzen – aber eben nur im Mittel.
Man erhielt die Anzahl  von Blumen auf
von Blumen auf  von knapp 180 Blumen, genauer von
von knapp 180 Blumen, genauer von
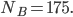
Verschiedene Bepflanzungsmöglichkeiten
Rike hat alles simuliert, berechnet und mit ihrem Muster 176 Blumen auf der Fläche  erhalten. Charly überlegt, dass man Rikes Muster spiegeln könnte
erhalten. Charly überlegt, dass man Rikes Muster spiegeln könnte
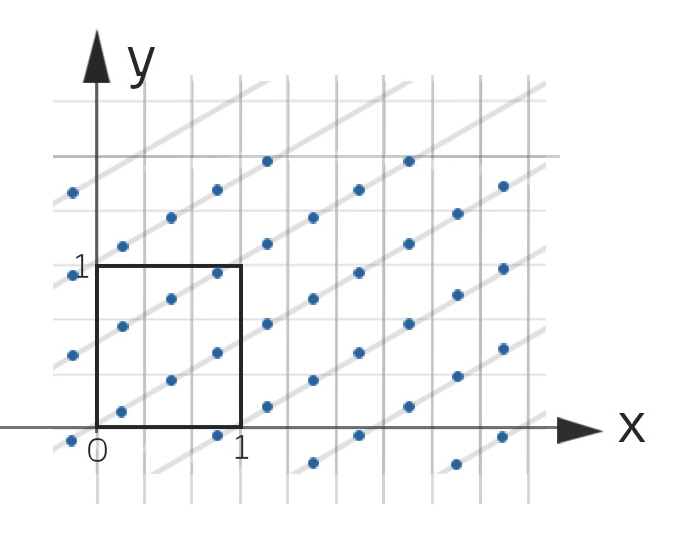
oder wie beim Würfel ein weiteres Muster erhält:
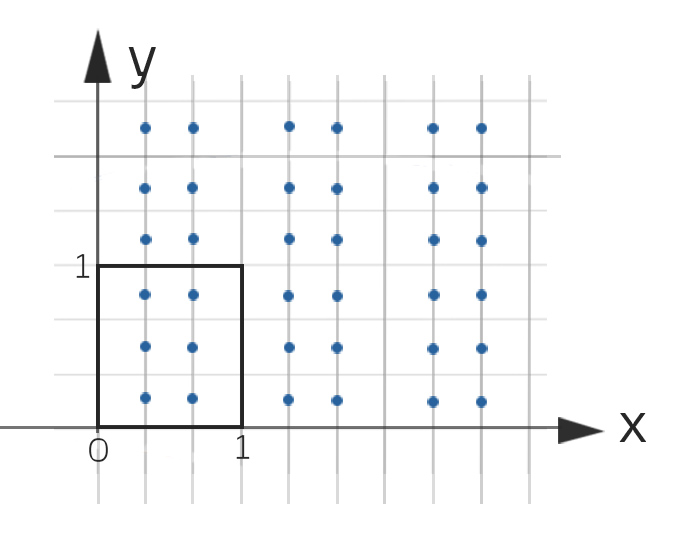
Sicher gibt es noch viel mehr Möglichkeiten. Wegen der gekrümmten Geometrie der Fläche  des Blumenbeetes kann es jedes Mal eine andere Anzahl von Blumen
des Blumenbeetes kann es jedes Mal eine andere Anzahl von Blumen  geben. Doch wie viele Blumenzwiebeln sollen nun bestellt werden? Kann man ein Minimum und ein Maximum berechnen?
geben. Doch wie viele Blumenzwiebeln sollen nun bestellt werden? Kann man ein Minimum und ein Maximum berechnen?
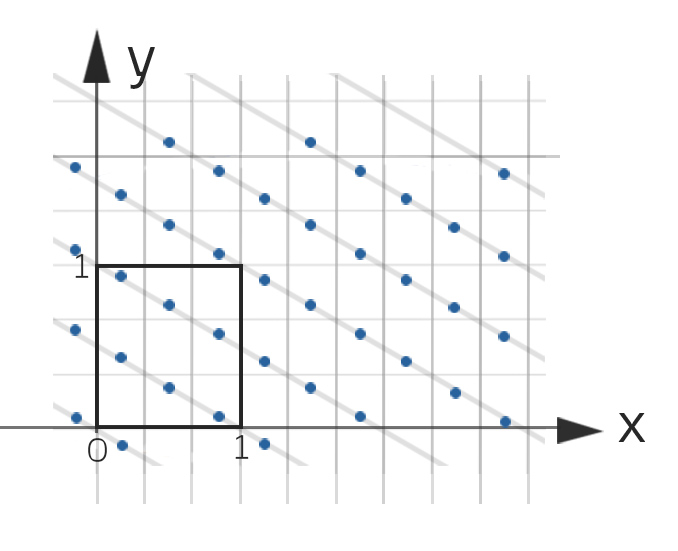
Charlys Zerlegung Z1 der Fläche
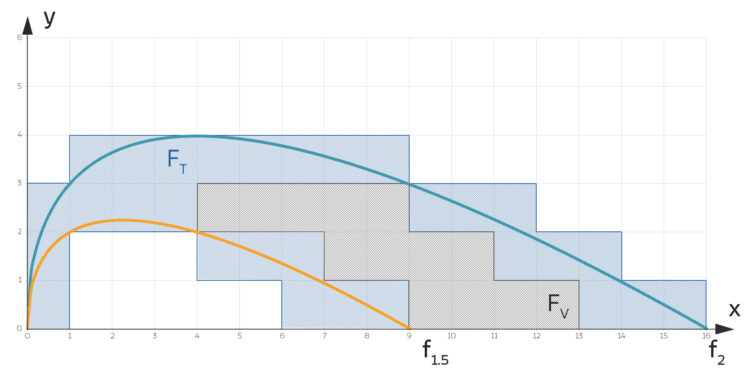
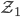 der Fläche
der Fläche  .
. 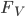 sind die Teile, die vollständig in
sind die Teile, die vollständig in  liegen,
liegen, 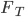 sind die Flächen, die teilweise in
sind die Flächen, die teilweise in  liegen.
liegen.Charly zerlegt die Fläche  in Quadrate von je 1 m² und beginnt am Nullpunkt des gegebenen Koordinatensystems. Auf diese Weise erhält er 13 Quadrate, die vollständig in
in Quadrate von je 1 m² und beginnt am Nullpunkt des gegebenen Koordinatensystems. Auf diese Weise erhält er 13 Quadrate, die vollständig in  liegen und die er zur Fläche
liegen und die er zur Fläche 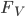 zusammenfasst. Außerdem erhält er 29 Quadrate, die teilweise in
zusammenfasst. Außerdem erhält er 29 Quadrate, die teilweise in  liegen, das ist die Fläche
liegen, das ist die Fläche 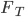 . Auf der Fläche
. Auf der Fläche 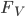 wird jedes Quadrat mit 6 Blumen/m² bepflanzt, und so erhält er das absolute Minimum
wird jedes Quadrat mit 6 Blumen/m² bepflanzt, und so erhält er das absolute Minimum 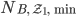 von Blumen, die gekauft werden müssen:
von Blumen, die gekauft werden müssen:
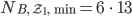
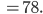
Das Maximum an Blumen 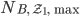
 liegende Quadrat ebenfalls mit 6 Blumen bepflanzt:
liegende Quadrat ebenfalls mit 6 Blumen bepflanzt:
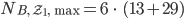
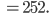
Jetzt kommt Rike dazu.
Rike Hey, Charly, was machst du?
Charlys statistischer Ansatz
Charly Hey, Rike, ich berechne die Anzahl der Blumen für das Beet unabhängig vom gewählten Muster. Ich nehme die Zufallsgröße 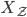 für die Anzahl der Blumen im gegebenen Beet. Für dieses
für die Anzahl der Blumen im gegebenen Beet. Für dieses 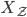 habe ich mit meiner Zerlegung hier herausgefunden, dass
habe ich mit meiner Zerlegung hier herausgefunden, dass
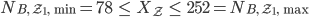
ist.
Rike Ah, also doch ein statistischer Ansatz für die Analysisaufgabe?
Charly Ja, es gibt doch ziemlich viele Lösungen, und irgendwie muss man doch ausrechnen, wie viele Blumen jetzt bestellt werden sollen.
Rike Haha. Jetzt hast du ein ziemlich breites Spektrum! Bei 252 wird es auf einigen Feldern ziemlich voll, stimmt‘s?
Charly Stimmt! Doch dafür ist ja die Statistik da, ich berechne den Mittelwert!
Charlys Mittelwert
Rike Welche Verteilung nimmst du denn?
Charly Naja, ich nehme an, dass jeder Wert 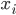 von
von 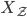 gleichwahrscheinlich ist, also die diskrete Gleichverteilung. Die Wahrscheinlichkeit
gleichwahrscheinlich ist, also die diskrete Gleichverteilung. Die Wahrscheinlichkeit 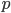 für jeden Wert
für jeden Wert 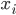
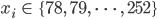
von 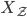 kriege ich, in dem ich 1 durch die Anzahl der möglichen Werte
kriege ich, in dem ich 1 durch die Anzahl der möglichen Werte 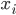 von
von 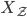 teile:
teile:
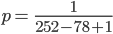
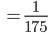
und den Mittelwert 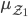 kann ich auch einfach berechnen:
kann ich auch einfach berechnen:
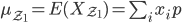
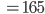
Rikes Fazit
Rike Okay, siehst du, dass der Mittelwert auch nicht zur Musterlösung passt?
Charly Ja, das sehe ich!
Rike Siehst du auch, dass deine Zerlegung 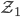 des Beetes ziemlich starr ist?
des Beetes ziemlich starr ist?
Charly Ja, das sehe ich, ich komme mir schon wie ein verblödeter Mathelehrer vor. Bei der Integralrechnung kommen auch Zerlegungen vor?
Rike Richtig. Beim Integral sollte man alle Zerlegungen prüfen.
Charly Gut. Ich habe mir überlegt, dass deine beiden Lösungen, die mit der zufälligen Bepflanzung in jedem Feld und die mit dem schrägen Muster, richtig originell und überzeugend sind und auch honoriert werden müssen.
Rike Bestehe ich jetzt doch das Matheabi?
Charly Haha, natürlich bestehst du das Abi, Rike, du hast es ja längst bestanden. Doch für meine Schülerinnen und Schüler mit solchen Ansätzen und Lösungen würde ich mich einsetzen.
Rike Toll!
***
Übungsaufgaben
- Berechne die Standardabweichung für diese Zerlegung
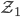 !
! - Welche sinnvollen Zerlegungen
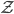 gibt es noch?
gibt es noch? - Welche Ergebnisse für
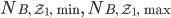 und
und 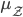 liefern diese?
liefern diese?
Lösungen
- 50.5
- Es gibt 7 verschiedene Zerlegungen eines Einheitsquadrates mit mind. 1 Blume/Teilfläche im Mittel
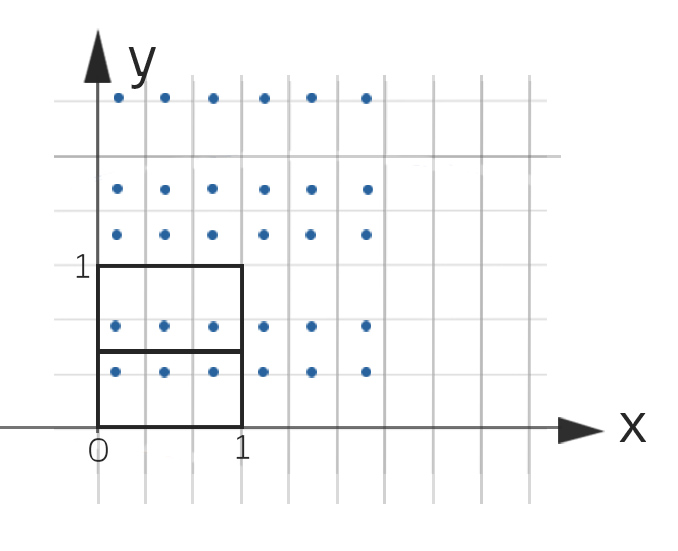
Zerlegung 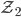 des Einheitsquadrates in zwei waagerechte Rechtecke mit je 3 Blumen pro halben Quadratmeter im Mittel
des Einheitsquadrates in zwei waagerechte Rechtecke mit je 3 Blumen pro halben Quadratmeter im Mittel
Weitere Zerlegung  des Einheitsquadrates in zwei senkrechte Rechtecke mit ebenfalls je 3 Blumen pro halben Quadratmeter im Mittel
des Einheitsquadrates in zwei senkrechte Rechtecke mit ebenfalls je 3 Blumen pro halben Quadratmeter im Mittel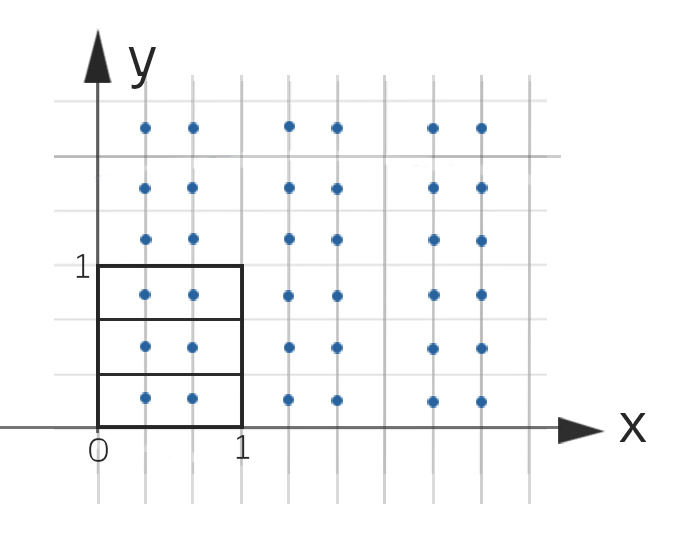
Zerlegung 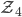 des Einheitsquadrates
des Einheitsquadrates
Zerlegung  des Einheitsquadrates
des Einheitsquadrates...
Außerdem kann die Position der Einheitsquadrate variiert werden.
- Für die Zerlegung
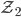 kann man die Flächen
kann man die Flächen 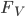 und
und 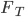 bestimmen:
bestimmen:
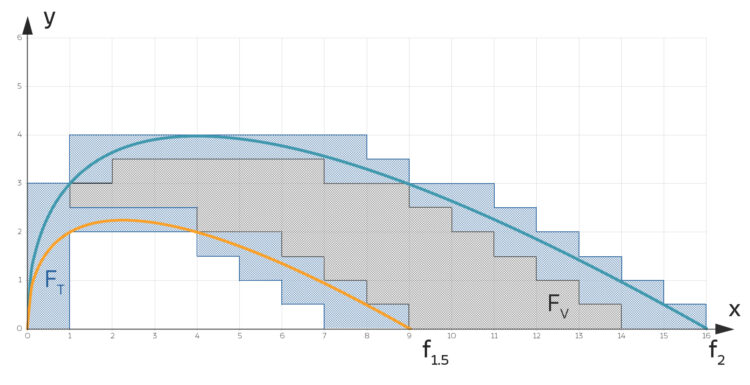
Flächen 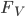 und
und 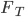 für die Zerlegung
für die Zerlegung 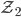
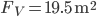
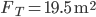
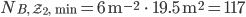
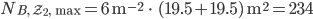

Das heißt, wie auch immer man die Blumen zu 3 Blumen je halben Quadratmeter pflanzt und das Beet in halbe Quadratmeter-Kästchen wie
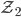 aufteilt, muss mindestens 117 Blumen und höchstens 234 Blumen kaufen. Im Mittel wären das 175.5 Blumen. (Die Originalaufgabe hatte 175 als Lösung)
aufteilt, muss mindestens 117 Blumen und höchstens 234 Blumen kaufen. Im Mittel wären das 175.5 Blumen. (Die Originalaufgabe hatte 175 als Lösung)
