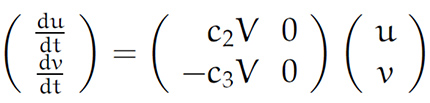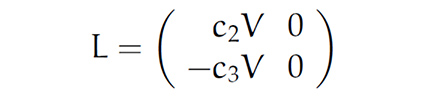Rike hat schwer mit der Hitze in Bielefeld zu kämpfen und kann nachts nicht schlafen. Sie surft ein bisschen im Netz und findet Artikel über gesperrte Badestrände wegen Blaualgenbefall. Das findet sie merkwürdig, sie hat das noch nie selbst erlebt. Sie recherchiert ein wenig und findet diese Blaualgen oder Cyanobakterien recht eigenwillig. Die haben mehrere Stoffwechsel: Nicht nur einen viel besseren als die gewöhnlichen Feld-, Wiesen und Nutzpflanzen, nein sie können sogar Licht mit noch ganz anderen Wellenlängen „verarbeiten” und nachts können sie Stickstoff „verarbeiten“. Den Stickstoff können sie aus der Luft verwenden und mit Phosphaten, die sie im Wasser des 21. Jahrhunderts finden, umsetzen. So sind sie sehr effizient und anpassungsfähig. Bei Wassertemperaturen ab 16°C geht ihr Stoffwechsel richtig los.
Rike stöhnt als sie auf der Seite des ZDF liest, dass diese Blaualgen sich „explosionsartig” fortpflanzen. Sie versucht, ein einfaches mathematisches Modell für das Wachstum der Blaualgen zu formulieren.
Blaualgenmodell mit den 2 Funktionen u und v
Da nimmt sie
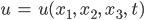
als (volumen- oder massemäßige) Konzentration von Blaualgen im Wasser und
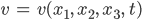
für die Konzentration aller Nährstoffe der Blaualgen im Wasser, beispielsweise der Phosphate.
Jetzt überlegt sie, wie sich die Konzentration der Blaualgen in einer kleinen Zeiteinheit ändert:
Sie nimmt durch Fortpflanzung zu, da könnte sie ein lineares Wachstum annehmen, das heißt, dass pro Zeiteinheit ein zur augenblicklichen Konzentration proportionaler Anteil hinzukommt. Das ist beim radioaktiven Zerfall so, siehe Dgln. für die 10. Klasse. Man hätte dann einen linearen Zuwachs, doch Rike möchte lieber einen nichtlinearen Zuwachs und wählt
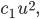
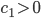. Außerdem gibt es einen Zuwachs an Blaualgen proportional zur Konzentration der Nährstoffe und proportional zur Konzentration der Blaualgen, das heißt, je mehr Blaualgen, je mehr gedeihen durch Futter, je mehr Futter, umso mehr Blaualgen, das ist ein typischer Räuber-Beute-Ansatz:
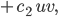
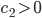. Beim Futter geht eben das verloren, und nur die Konstante kann anders sein. Je mehr Blaualgen, je weniger Futter, je mehr Futter, umso stärker die Abnahme:
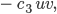
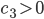. Rike denkt sich, dass die Blaualgen im Wasser diffundieren, mit einem Diffusionskoeffizienten 
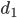und ebenso die Nahrung mit dem Diffusionskoeffizienten 
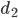. So kommt man zu einem System von partiellen Dgln:
Partielle Dgln. für Blaualgen
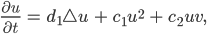
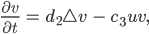
steht für die Summe der zweiten partiellen örtlichen Ableitungen.
Rike denkt, na gut, gibt‘s denn da Gleichgewichtslösungen?
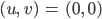
ist eine Lösung denkt Rike, keine Nährstoffe, keine Blaualgen, das passt. Gleichgewichtslösungen sind solche, die zeitlich konstant sind, also im Gleichgewicht. Gibt es noch andere? Ja, für
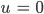
ergibt das System aus den 2 pDgln.
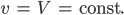
Nun betrachtet Rike das System ganz lokal in der Nähe dieser Lösung
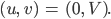
Dazu vernachlässigt Rike die Diffusion und bestimmt den linearen Anteil in der Nähe der Gleichgewichtslösung
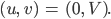
Lineare gewöhnliche Dgl. für Blaualgen
So erhält Rike die linearen Dgln:
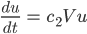
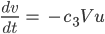
oder in Matrixschreibweise:
Instabilität des Systems nahe (0, V)
Die Matrix L:
hat die Eigenwerte
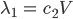
und
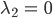
Für eine Stabilität des nährstoffhaltigen, aber Blaualgen-losen Zustandes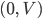 
müssten beide Eigenwerte negativ sein. Daraus folgt, dass der Gleichgewichtszustand, für den Rike nur 
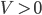zulässt (positive Werte der Nährstoffkonzentration), nicht stabil ist. Das System wird sich bei der kleinsten Änderung aus diesem Zustand heraus bewegen. Das heißt, wenn sich eine kleinste Anregung 
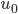von Blaualgen im nährstoffhaltigen Wasser findet, reagiert das System darauf durch Blaualgenwachstum und -vermehrung. Rike freut sich, dass sie so ein einfaches System gefunden hat, welches wesentliche Eigenschaften der Blaualgen widerspiegelt.
Anfangsanregung
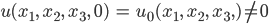für einige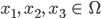 
Randbedingungen
Sie muss noch das Verhalten der Funktionen auf dem Rand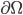 
des betrachteten Gebietes 
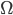beschreiben.
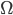) zur Wasseroberfläche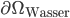 
Wie wäre es, wenn wir einen großen See betrachten.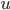 
sollte an der Wasseroberfläche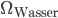 
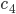) Abstoßung und eine teilweise (
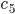) tangentiale Verteilung der Blaualgen hätten?
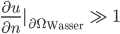
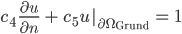
Und die Nährstoffe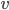 
? Die werden von den Rändern des Gebietes senkrecht reflektiert:
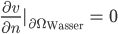
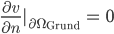
Rike fragt sich, ob man so ein Verhalten gut mit einem Partikelsystem simulieren kann und probiert es aus.
Übungsaufgabe
Welche Aspekte sind gut simuliert, welche nicht?
Lösung
+ … nichtlineares (quadratisches) Wachstum pro Zeiteinheit
- … Temperaturabhängigkeit fehlt