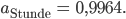Dgln in der 10. Klasse - mathezartbitter

Max und Rike sind in den Osterferien an die Nordsee gefahren. Beim Beachvolleyball haben sie einen neuen Freund kennengelernt: Charly (30). Er hat Sport studiert und arbeitet als Animateur. Doch jetzt will er als Quereinsteiger Mathe/Sportlehrer werden. Außer Sport mag er Kinder und Mathe. Er hat sich alle Matheschulbücher besorgt, geht sie durch und wundert sich. Heute diskutiert er mit Rike und Max eine tolle Aufgabe über Halbwertzeit.

Wachstums- und Abnahmeprozesse

Charly Rike, hier habe ich eine Aufgabe zu Wachstums- und Abnahmeprozessen:

Bei der Reaktorkatastrophe von Fukushima im Jahre 2011 gelangten die radioaktiven Stoffe Iod 131, Cäsium 134 und Cäsium 137 ins Meer.

Iod 131 ist sehr kurzlebig und hat eine Halbwertszeit von rund 8 Tagen. Berechne jeweils den Abnahmefaktor pro Tag und Stunde.
…

Max Ist denn Halbwertszeit erklärt?

Charly Ja, hier:

Halbwertszeit: Zeitspanne, in der die Ausgangsmenge durch Zerfall auf die Hälfte gesunken ist.

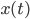
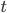
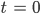
Rike Ist ja stark! 10. Klasse? Warte mal, ich muss kurz überlegen, okay. Lass uns mal als Bezeichnung für die Anzahl der Ionen zur Zeit nehmen. Bei lassen wir den Zerfall starten.

Charly Okay, machen wir.

Aufstellen der Dgln

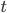
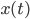
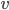
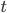
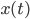
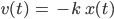
Rike Die Anzahl der Iod-Atome verringert sich proportional zu ihrer Anfangsanzahl, denn in 8 Tagen haben wir ja nur noch die Hälfte, egal, wie viel das ist. Und weil Du in jedem Augenblick die Ionenanzahl als neue Anfangsanzahl nehmen kannst, ist die Verfallsgeschwindigkeit zu jeder Zeit proportional zur augenblicklichen Anzahl , Charly:

oder

für Zerfallsprozesse.

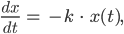
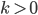
Charly Okay, verstehe. 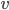ist die Geschwindigkeit, oder wie sich die Konzentration verändert. Je mehr Ionen da sind, umso mehr verfallen.

Rike Richtig. Nur,

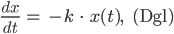
ist eine gewöhnliche Diffenzialgleichung. Machst Du das echt in der 10. Klasse?

Charly Naja! Ich sehe das sportlich. Ich mache keinen Kindergartensport und auch keine Behindertenmathe mit einer 10. Klasse! Was brauche ich mathematisch dazu?

Anfangswert

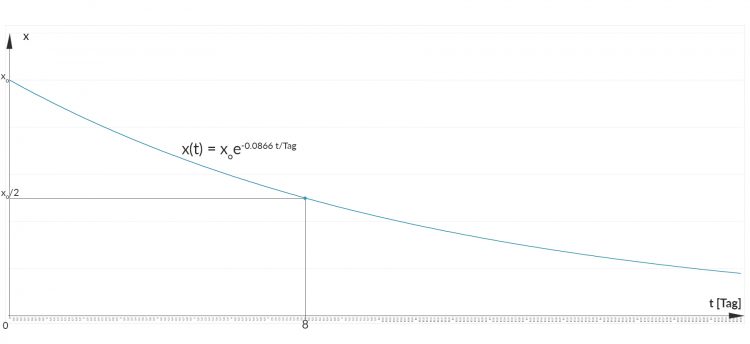
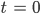
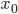
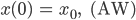
Rike Warte, ich zeigs Dir. Wenn wir die Menge zur Zeit mit bezeichnen:

dann hast Du einen Anfangswert und die Dgl. mit diesem Anfangswert ist eine Anfangswertaufgabe AWA (= Dgl + AW). Solche haben genau eine Lösung.

Lösung der Anfangswertaufgabe

Max Bloß gut!

Charly Bloß gut!

Rike Das geht so

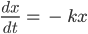
Mit einfachem Umformen gehts weiter, da siehst Du, wie stark das Kalkül ist:

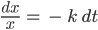
Das integrierst Du. Dann ist

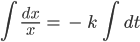
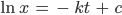
und stellst es nach um:

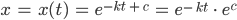
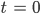
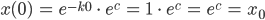
Dann setzt Du noch den Anfangswert für ein:

also ist

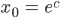
und die Lösung der Anfangswertaufgabe ist

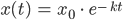
Charly Wow!

Parameterbestimmung

Rike Jetzt müssen wir noch dieses bestimmen:

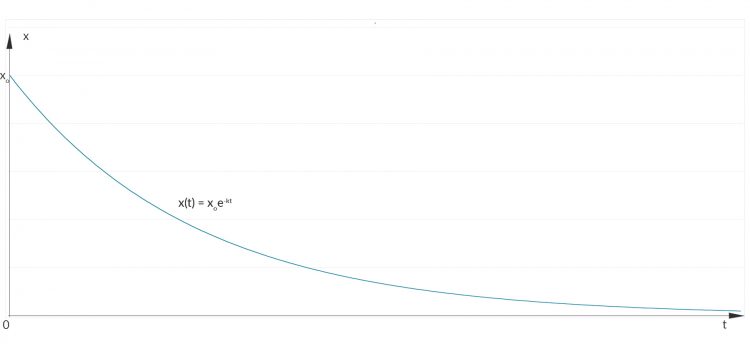
Max Ja, wir wissen, dass die Halbwertszeit 8 Tage ist.

Rike Stimmt. Wir schreiben, dass zur Zeit

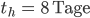
die Hälfte von der Anfangsmenge da ist:

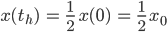
Charly Ja!

Rike Und andererseits berechnen wir mit unserer Lösung die Menge der Ionen zur Zeit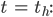

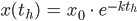
Die beiden Ausdrücke setzen wir gleich:

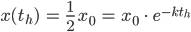
Max Rike, da kannst Du 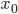kürzen!

Charly Das kann ich auch!

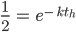
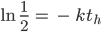
Jetzt stelle ich nach um und kriege

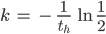
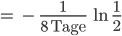
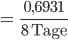
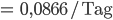
Rike Toll!

Abnahmefaktor

Charly Aber den Abnahmefaktor pro Tag und Stunde?

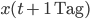
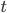
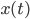
Rike Du rechnest das Verhältnis von der Ionenanzahl einen Tag später zur Ionenanzahl zur Zeit , also , aus!

Charly Ja, kann ich machen.

Rike Lass uns noch einen Namen für diesen Abnahmefaktor finden

Charly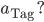

Rike Okay

Charly

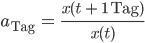
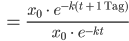
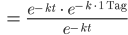
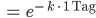
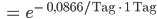
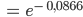
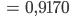
Max Super, Charly, Du kannst das Deiner 10. Klasse bestimmt gut vorrechnen! Ihr werdet Sieger im Pisa-Test!

Charly Hahaha, ich brauche den Begriff der Geschwindigkeit, der ist bekannt, dann Rikes tolle Herleitung, dazu die Stammfunktion und die Expotentialfunktion. Das ist doch zumutbar. Wollen wir jetzt ins Wasser gehen?

***

Übungsaufgabe

Bestimme den Abnahmefaktor für eine Stunde!