Horizont als Zufallsweg

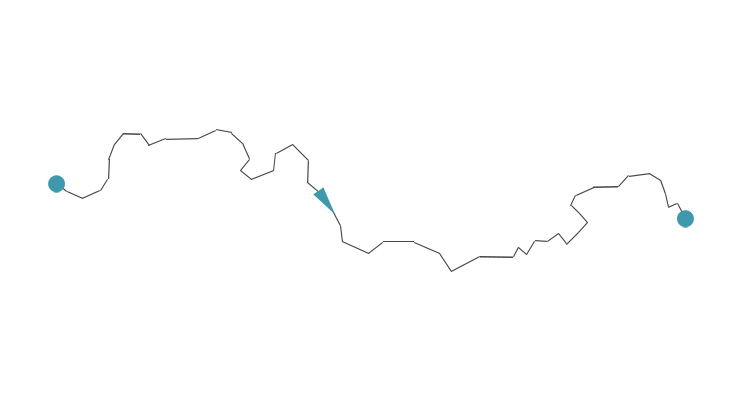
Überaus leidenschaftlich berichtet Kevin Hartnett in seinem Überblicksartikel A Unified Theory of Randomness von neuen Zugängen zur Beschreibung zufälliger Prozesse. Hartnett schreibt in diesem Artikel über Scott Sheffields neue Theorien zufälliger Wege, Formen und Geometrien. Diese Theorie ist vor allem physikalisch motiviert, denn man will die Pfade von Elementarteilchen genauer beschreiben und hat dazu die sogenannte Theorie der Liouville Quantum Gravity geschaffen. Andererseits gibt es seit längerem die Theorie der Brownschen Bewegung. Schließlich haben Sheffield und Miller in mehreren Artikeln gezeigt, dass diese beiden Zugänge prinzipiell dasselbe sind.

Neue Zufallswege-Theorien

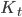
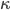
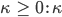
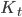
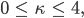
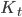
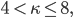
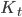
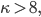
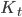
Mathematisch liegt dem Allem die Stochastische Loewner Evolution (SLE) zugrunde. Das ist ein stochastischer Prozess des Wachstums einer Menge (mit der Zeit t). In einfachen Fällen kann man damit den random walk, also einen zufälligen Weg mit der Zeit als Parameter beschreiben. Diese SLE werden normiert und haben schließlich nur noch einen Parameter: (Kappa), ist die Geschwindigkeit der Bownschen Bewegung. Diese Menge soll in einem einfach zusammenhängenden Gebiet G sein und zwei Punkte darin verbinden. So gibt es prinzipiell 3 Szenarien:

1. die Menge besteht aus einer einfachen Kurve.
2. die Menge ist eine sich selbst schneidende Kurve, die aber die Fläche G nicht ausfüllt.
3. die Menge bildet eine Kurve, die G ausfüllt.

Doch nicht nur in der mikroskopischen Welt der Moleküle und Elementarteilchen findet man solche Brownschen Bewegungen, nein, man findet sie sehr oft, eigentlich überall, meinen die Stochastiker. So schreibt Hartnett, dass die Flugbahnen, die verschiedene Flugzeuge zu einem festen Ort fliegen, bei einer konstanten Höhe über dem (zufälligen und sich geometrisch ändernden) Grund – korrigiert um die Erdkrümmung, sehr stark Pfaden von Partikeln mit Brownschen Bewegungen ähneln.

Dies hat uns Hoffnung gemacht, solche Flugzeughöhentrackings auf kleinere Objekte zu übertragen und dann ebensolche SLE-Kurven zu finden.

Wir benutzen dazu ausgewählte Landschaftsfotos, deren Originale uns vorliegen, analog und digital fotografierte. Die Negative der analogen Fotos wurden eingescannt und weisen nun ebenfalls eine diskrete Struktur auf. In Analogie zu den Höhenlinien der Flugzeuge über Grund haben wir in diesen Landschaftsfotos nun den Horizont als Kurve bestimmt. Mit Horizont meinen wir die Linie zwischen Himmel und „Erde“.

Fangen wir mit Bild 1 an: Beim Meer ist der Horizont vielleicht am einfachsten zu bestimmen.

1. Problem: Horizont ist nicht im Fokus

Die Horizontlinie ist doch nicht so einfach zu bestimmen, da sie beim Fotografieren offensichtlich nicht im Fokus war. Tatsächlich sind die Details (Wellen) am Horizont nicht zu erkennen. Die Horizontlinie wird also durch einen Bereich gelegt, in dem Details nicht zu erkennen sind. Als Approximation erhält man dann eine Kurve mit wenigen Richtungsänderungen, also eine glatte Kurve.

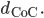
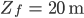
Beim 2. Foto kann das genauer berechnet werden, denn hier liegen die Metadaten vor. Wir benutzen die Formel für den Circle of Confusion Wir haben auf die Bildmitte scharfgestellt, also ca.

Der Horizont Z liegt bei ca. 100m,

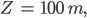
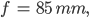
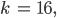
ergeben eine Breite des Bildpunktes am Horizont Z von

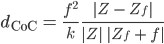
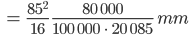
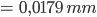
Das sind

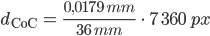
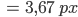
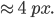
Das heißt, ein Punkt am Horizont wird im Bild 4 px breit.(*) – Unser Horizont hat im 2. Foto eine Ungenauigkeit von 4 px.

2. Problem: Horizont als Linie

Die Horizontlinie hat eine gewisse Dicke, hier immer 4 px (*), die mit den Details konkurriert. Ist die Auflösung kleiner – wie beim Foto 3 (Handyfoto, längste Seite: 3264 px), so sind einfach nicht genug Pixel da, um die Linie und die Details abzubilden.

3. Problem: Weitere Unschärfen

Im folgenden Foto Nr. 4 gibt es eine weitere Spezifik. Neben der Unschärfe am Horizont gibt es weitere Objekte, die noch viel unschärfer abgebildet werden, wegen der Unschärfe in der Tiefe, wegen der Bewegungsunschärfe oder wegen des Objektivs. Hier ist es eine Plastiklinse, die einen besonderen Look erzeugt. Umgekehrt kann man aus den Metadaten – sofern sie vorliegen, hier im analogen Foto natürlich nicht – und glatten Horizontkurven auf Entfernungen, Objekte und Objektive schließen.

4. Problem: Konstruktion des Horizonts

Im Bild 4 sieht man rechts – durch den Baum hindurch – Himmel. Hier könnten wir geschlossene Linien bilden, die die Grenze von Himmel und „Erde“ beschreiben. Solche haben wir vernachlässigt. Zugelassen ist lediglich, dass sich die Horizontlinie mit sich selbst berührt.

Bei den folgenden analogen Fotos 5 und 6 wird die Detailauflösung auch durch das Filmkorn des Films sowie durch Parameter des Scans beeinflusst.

Offensichtlich habe große, glatte Gesteinsbrocken weniger Details als Bäume.

Zusammenfassung

Welche Eigenschaften haben unsere zufälligen Pfade?

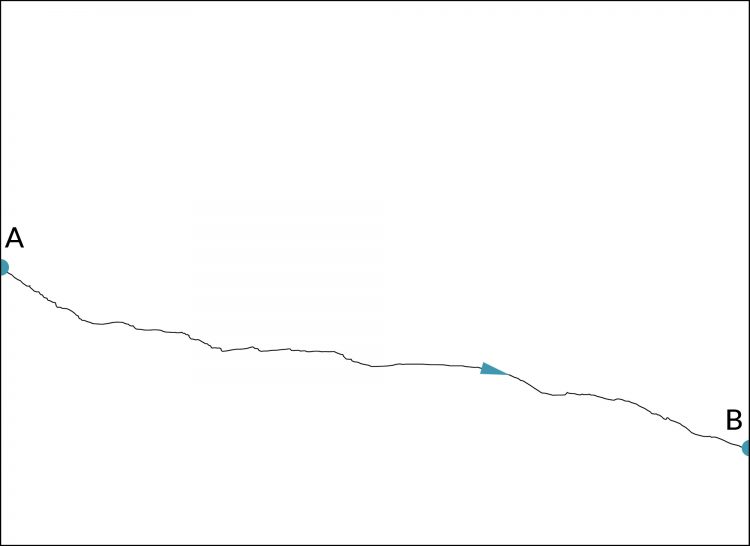
1. Sie sind alle stetig, und zwar aufgrund unserer Konstruktion und Bildauswahl. Der Horizont ist immer eine zusammenhängende Linie.
2. Wir können die Pfade gut als Brownsche Bewegung ansehen. Sie startet in einem festen Punkt A und geht nach B. Jeder Zuwachs, d.h. jeder noch so kleiner Schritt, kann als unabhängig und Standard-normalverteilt betrachtet werden.
3. Nehmen wir an, die Pfade genügen den mathematischen Voraussetzungen der SLE. Dann ist Wir haben eine einfache Linie. Es ist falls sich die Linie selbst berührt.
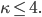
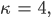
4. Man könnte den fraktalen Charakter der Kurven näher bestimmen, und zwar mittels Hausdorff-Dimension D. Dazu versucht man, die Kurve mit N Kugeln vom Radius r zu überdecken und bildet den Grenzwert:

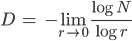
   Eine „einfache“ Kurve hat die Hausdorff-Dimension Die Kurven des SLE-Prozesses haben

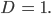
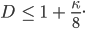
   Wegen der endlichen Auflösung und der Unmöglichkeit, den Radius r nach 0 gehen zu lassen, können wir den Grenzwert nicht bilden.

5. Die Auflösung von Details und damit von Richtungsänderungen eines Pfades hängen von der Bildauflösung ab. Ein Bild mit 10 000 x 10 000 px kann mehr Richtungsänderungen haben als ein kleines.
6. Die abgebildete Schärfe des Horizonts wirkt sich auf die Anzahl der Richtungsänderungen ab. Das lässt sich mit dem Circle of Confusion bestimmen.
7. Die Güte des Objektivs wirkt sich auf die Anzahl der abgebildeten Richtungsänderungen ab.
8. Letztlich hat die Geometrie (als das Urbild) Einfluss auf die abgebildete Horizontkurve.

(*) Die Rechnungen beziehen sich auf die Originalgrößen. Auf der Website sind allerdings nicht die Originale, sondern "kleiner gerechnete" Bilder. Nur Foto 3 ist unverändert.

[Teil II]

***

Übungsaufgaben

1. Welche mathematischen Möglichkeiten gibt es, die Anzahl der Richtungsänderungen zu bestimmen?
2. Wie könnte man für das folgende Bild den Horizont festlegen?

Lösung

2.