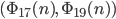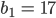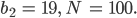Max und Rike machen einen Osterspaziergang, doch leider fängt es an zu regnen. Max fragt Rike, ob sie so etwas auch simulieren könnte, der Regen sieht so gleichmäßig aus, bildet aber kein Muster. Rike erklärt ihm die Van-der-Corput-, Halton- und Hammersleyfolgen, die man für gleichmäßiges Licht in der Computergrafik oder für numerische Integration benutzt.
Max Hey, so ein Regen! Sag mal Rike, kannst Du sowas simulieren?
Rike Ja, so ein Regen! Ich find‘s schön! Ich wäre glücklich, wenn ich das so gut simulieren könnte. Doch es gibt ein paar mathematische Ideen dazu.
Max Ja?
Rike Diese Gleichmäßigkeit ohne Musterbildung ist eine echte Herausforderung. Die erste Idee dazu kam von van der Corput. Dazu muss man ein Zahlensystem wählen.
Max Also, ich liebe das Dezimalsystem!
Darstellung von n im b-System
Rike Okay. Also, Du wählst eine Basis b und kannst jede Zahl n in Potenzen von 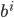
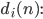
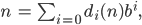
und die Koeffizienten 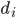
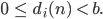
Max Hmmm.
Rike Ach, im Dezimalsystem bedeutet das, dass Du Ziffern 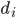
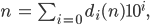
zum Beispiel ist
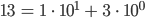
und
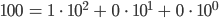
Max Stimmt!
Inverse Radical Function
Rike Und aus dieser Darstellung findet man die inverse radical function, das ist eine Abbildung, die jeder Zahl n die inverse Darstellung zuordnet:
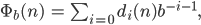
das erklär ich Dir mal: Du nimmst also die Ziffern 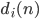
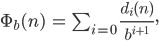
die kleinste Potenz 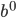
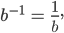
der Koeffizient 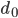
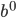
Max Was wird dann aus 13?
Rike Die Reihenfolge der Ziffern ändert sich zu 31, der Wert wird:
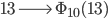
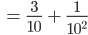
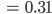
Max Okay, verstehe, aus 100 wird dann
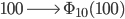
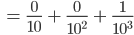
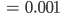
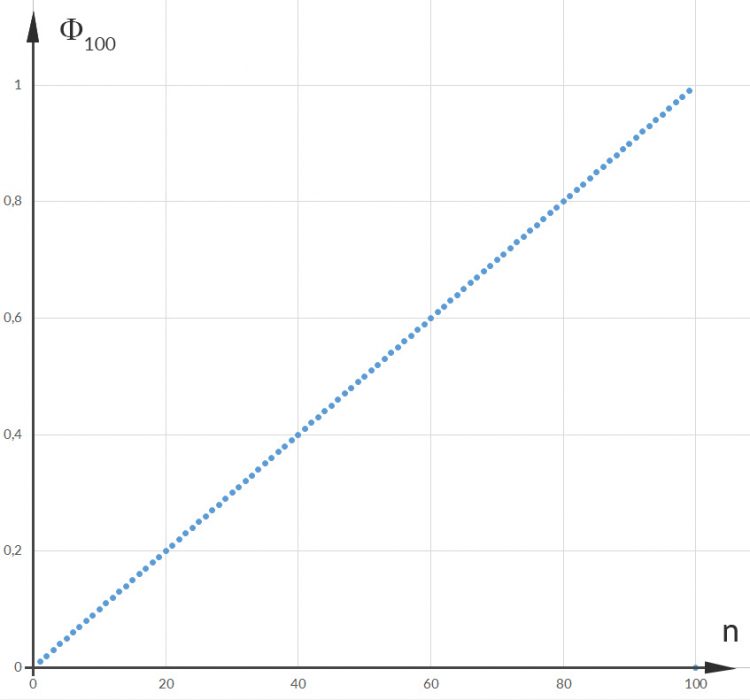
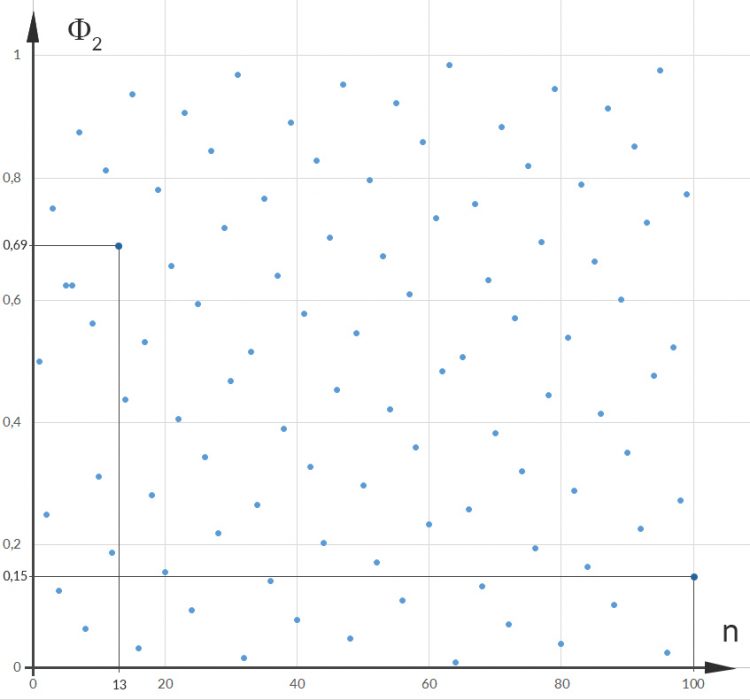
Rike Richtig! Das gibt folgendes Bild für die ersten 100 Zahlen zur Basis 10:
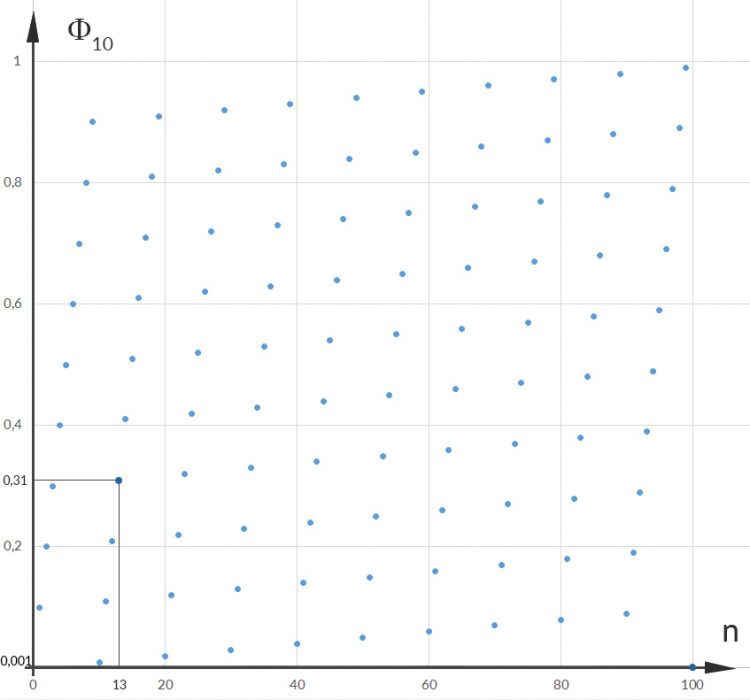
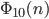
Max Okay, verstehe, sieht aber noch lange nicht wie unser Osterregen aus.
Rike Haha, stimmt, er ist viel zu regelmäßig. Halton hat dann die Basen gewechselt. Viel besser ist das Binärsystem, das kennst Du doch?
Beispiel im Binärsystem
Max Okay,
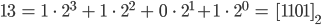
und
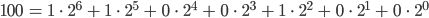
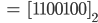
Rike Max, das machst Du toll! Die radikal inverse Darstellung ist dann
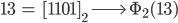
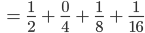
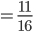
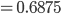
Und
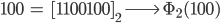
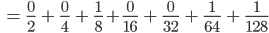
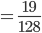
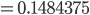
Max Verstehe!
Rike Und das Bild sieht schon sehr gut aus:
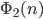
Max Hey, das gefällt mir!
Hammersley-Punkte
Rike Aber es noch nicht zufällig genug. Hammersley hat dann vorgeschlagen, solche Punkte im s-dimensionalen Raum zu konstruieren, wo jede Komponente einer anderen Halton-Folge angehört, also
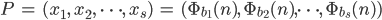
Max Kannst Du denn nicht mal ein paar solche Bilder ausrechnen?
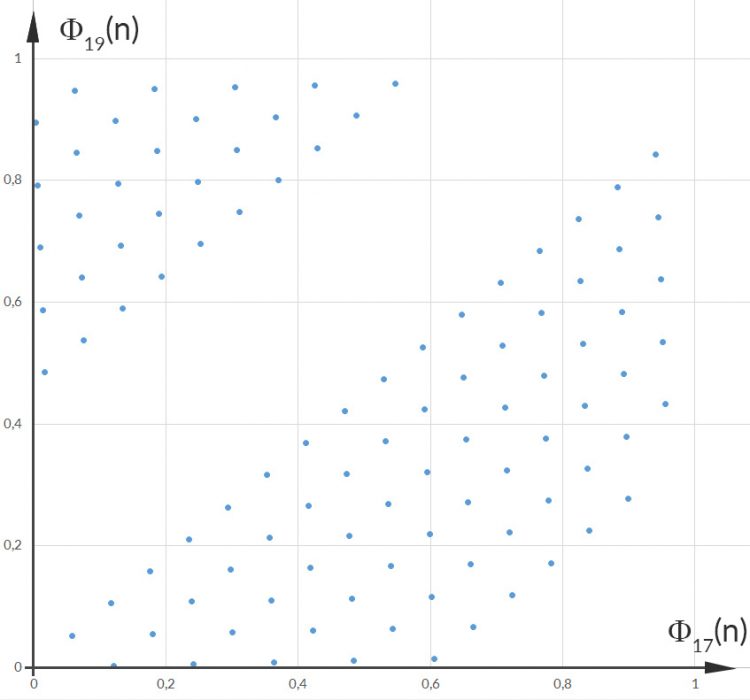
Rike Ja, klar, hier:
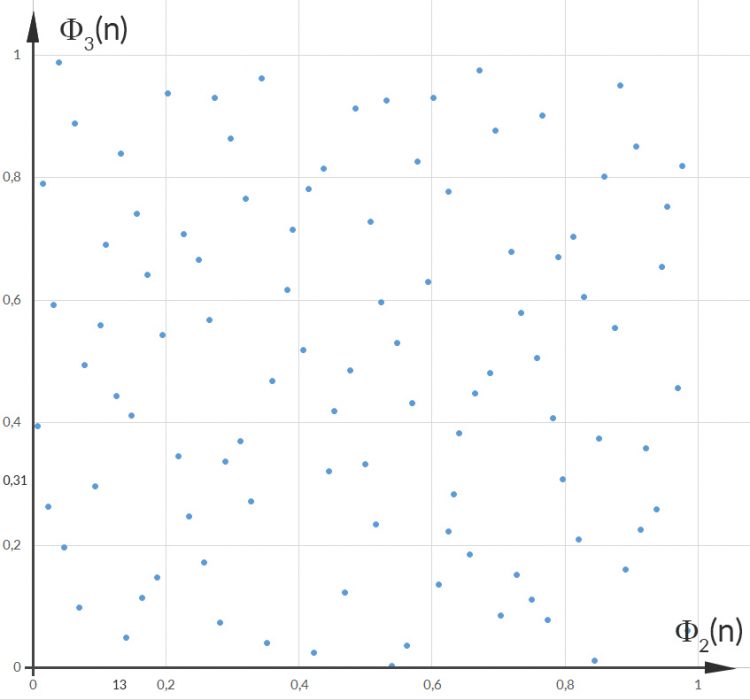
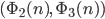
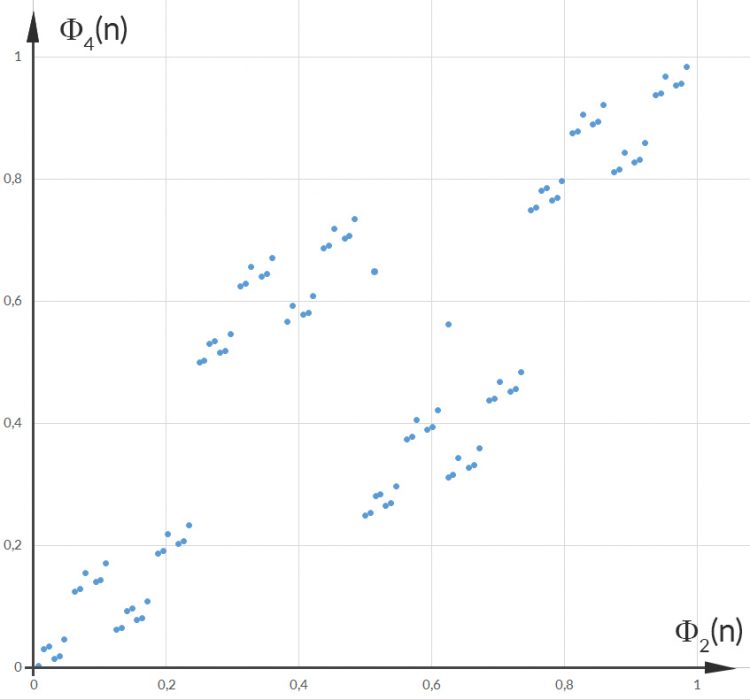
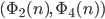
Max Okay, jetzt versteh‘ ich langsam, das Muster mit den Basen 2 und 3 sieht schon wie Regen aus, das mit 2 und 4 gar nicht, das sieht wie Hagel aus.
Rike Stimmt! Solche Folgen wurden ausgiebig untersucht, und am besten nimmt man für gleichmäßige Verteilungen Basen, die teilerfremd sind. Dann gibt es ein paar Kriterien, um ihre Güte zu vergleichen.
Max Ja?
Numerische Integration mit zufälligen Folgen
Rike Ja, als erstes fragt man, ob man bei der 1-dimensionalen Folge, wenn man die Punkte als Näherung fürs Intergral benutzt, auch wirklich eine Näherung des Intergrals herausbekommt:
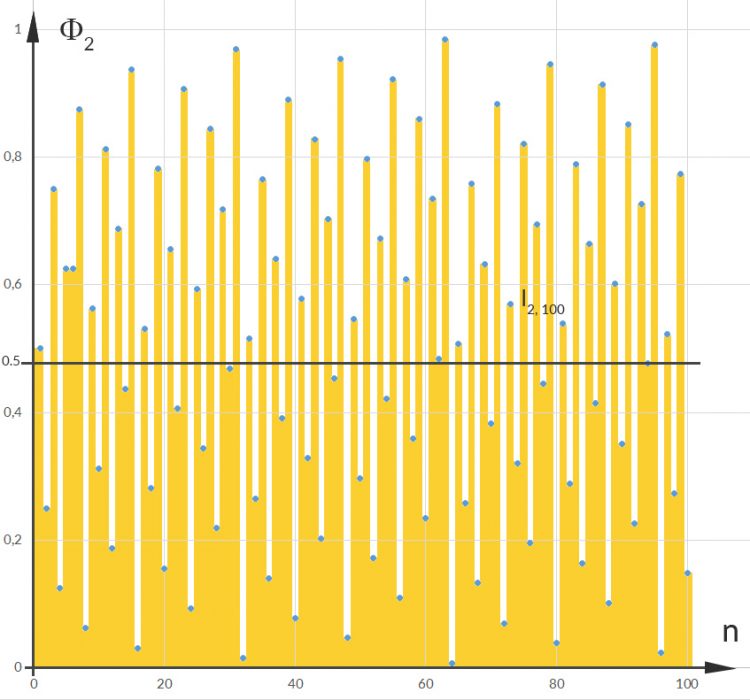
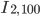
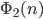
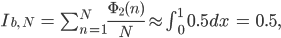
dabei ist N ist die Anzahl der Punkte n.
Max Okay, und wie gut ist das beim Binärsystem und beim Dezimalsystem?
Rike Beim Dezimalsystem ist die Näherung des Integrals
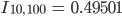
und fürs Binärsystem ist das
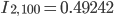
Max Also, das Dezimalsystem nähert besser?
Diskrepanz
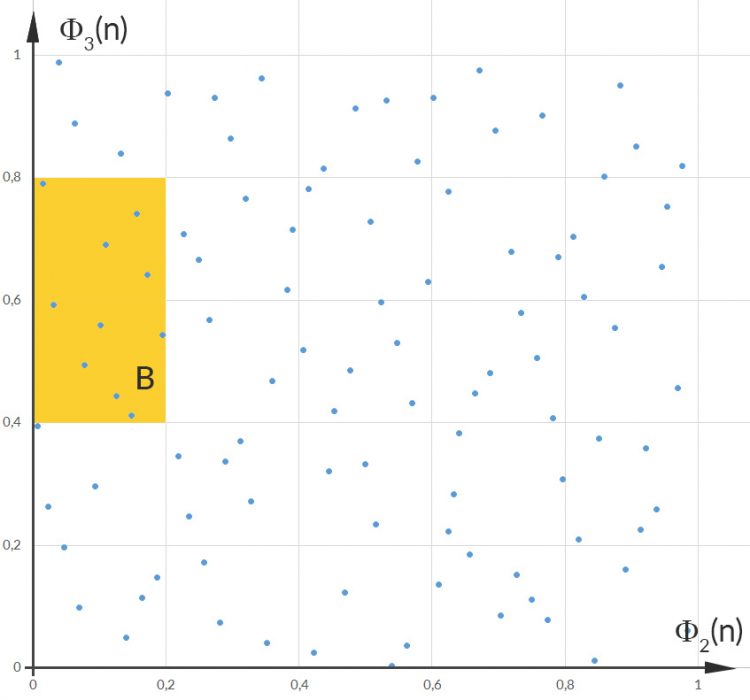
Rike Ja, diese Näherung ist besser. Aber es gibt noch ein weiteres Kriterium für die Hammersley-Punkte. Wenn wir also 2 solche Folgen 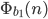
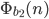
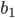
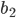
Max Verstehe, bei 2 und 4 gibt es Kästchen, in die nichts fällt.
Rike Stimmt. Man zählt also die Punkte, die in Kästen fallen. Die Zahl in jedem Kästchen nennt man üblicherweise 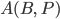
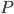
Max Okay.
Rike Diese Zahl A teilt man durch die Gesamtzahl der Punkte und berechnet davon die Differenz zum Flächeninhalt 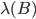
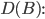

Max Okay.
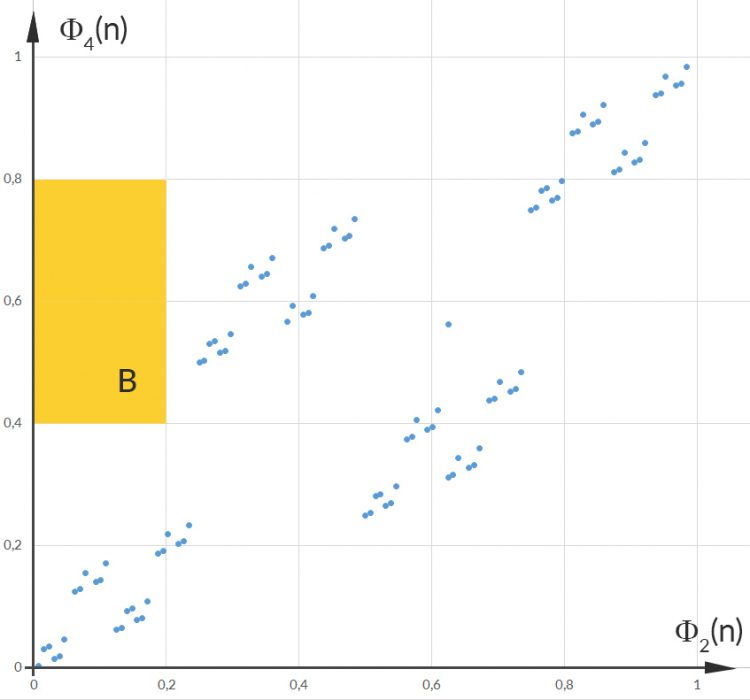
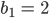
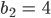
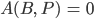
Für die gelbe Fläche B bekommen wir
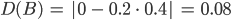
Und beim Fall 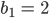
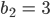
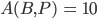
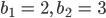
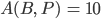
Dann ist
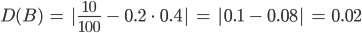
Max Okay.
Rike Jetzt musst Du nur noch alle möglichen Kästchen untersuchen und das Maximum, genauer ist es eigentlich das Supremum, der Differenz bilden, das ist dann die sogenannte Diskrepanz.
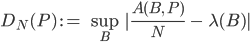
Max Verstehe, so eine Art größter Fehler.
Rike Ja, alle Kästchen sollen Punkte haben. Und diese Hammersley-Punkte eignen sich sehr gut zur Simulation von Regen, für sehr große N wird nämlich diese Diskrepanz immer kleiner, er geht nach Null für teilerfremde 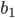
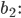
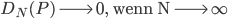
Max Boah, das ist wirklich genial.
***
Übungsaufgaben
- Bestimme die 1- dimensionale Halton-Folge
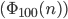
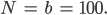
- Bestimme die Hammersley-Folge