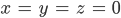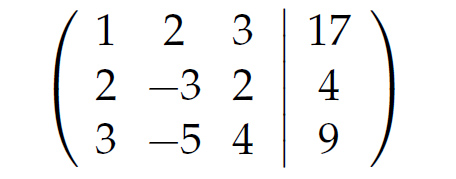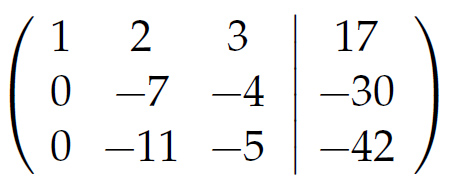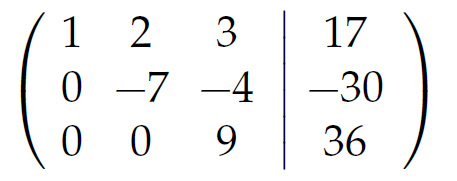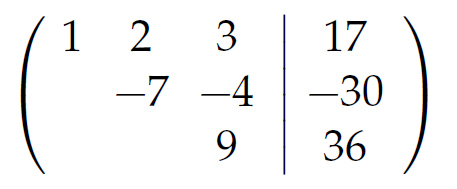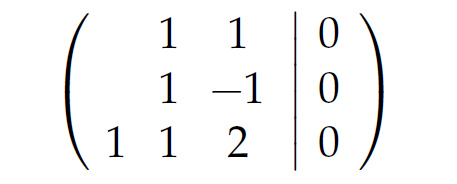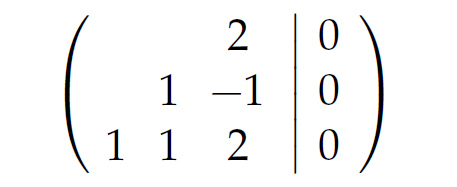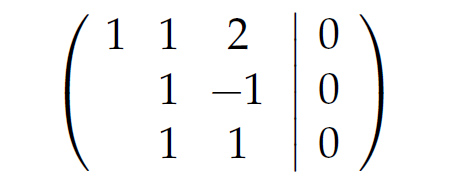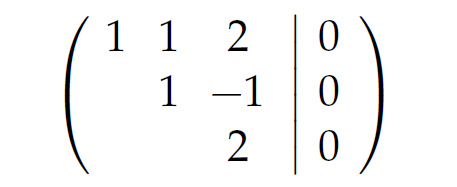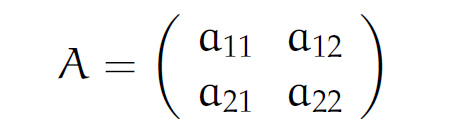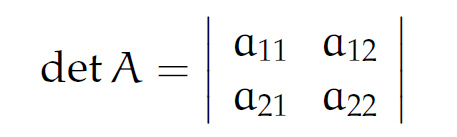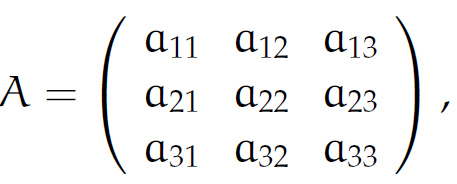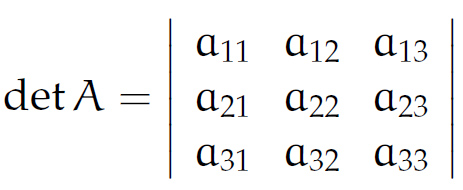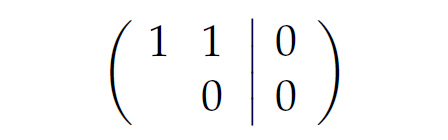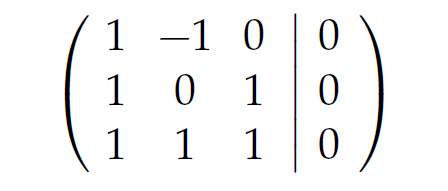Rike und Charly sitzen beim Beachvolleyballplatz und schauen in ein Mathebuch. Max tut was für seine Ausdauer und joggt am Strand (2 x 8 km).
Charly Schau mal Rike, sehr weit vorn im Buch wird der Gauß-Algorithmus anhand eines Beispiels vorgestellt. Vorher wurde das Additionsverfahren besprochen. Da steht, dass bei einem linearen Gleichungssystem Mehrfache einer Zeile zu Mehrfachen einer anderen addiert werden können ohne dass sich die Lösungsmenge ändert.
Rike Richtig.
Lehrbuchbeispiel
Charly Hier ist das Beispiel
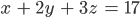
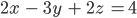
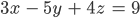
Rike Wollen wir das nicht mal in Matrixschreibweise diskutieren?
Charly Okay, wie geht das?
Rike Wir schreiben nur die Koeffizienten von x, y und z in eine Matrix. Die rechte Seite des Gleichungssystems trennen wir mit einem senkrechten Strich:
Charly Okay
Rike Nun wird das -2-Fache der ersten Zeile zur 2. addiert, damit nämlich x verschwindet, und das -3-Fache der 1. Zeile zur 3. Zeile. Dann erhält man
Rike Die 42 ist nett.
Charly Stimmt. Und jetzt nehmen wir noch das -11-Fache der 2. Zeile und addieren es zum 7-Fachen der dritten Zeile:
Die Form nennt man Dreiecksform.
Rechte obere Dreiecksform
Rike Stimmt, genauer: rechte obere Dreiecksform. In dieser Schreibweise ist es erlaubt, die Nullen wegzulassen, dann sieht man die Dreiecksform gut:
Charly Okay, jetzt kann man zuerst z bestimmen
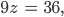
also
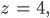
dann “nach oben gehen” und mit z auch y bestimmen
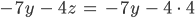
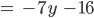
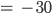
und so
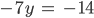
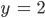
Aus der 1. Gleichung erhälst Du schließlich x:
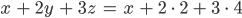
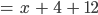
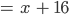
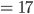
Also ist

Rike Gut.
Charly Das Beispiel hat eine Lösung:
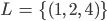
Rike Hmmm, war‘s das dann schon? Ist das alles zum Gauß-Algorithmus? Du musst noch mehr wissen, sonst geht das schief.
Charly Was denn?
Rike Beim Gauß-Algorithmus nimmt man tatsächlich Mehrfache einer Zeile zu Mehrfachen anderer Zeile, wie Du schon verstanden hast, und zwar ganz systematisch Mehrfache der 1. Zeile zu Mehrfachen der 2. und zur 3. Zeile, um x in der 2. und 3. Zeile zu eliminieren, und danach geeignete Mehrfache der 2. Zeile zu Mehrfachen der 3. Zeile, um y zu elminieren. Das Ziel ist die rechte obere Dreiecksmatrix.
Charly Na gut.
1. Gegenbeispiel
Rike Schau mal, ich geb' Dir mal 'ne Aufgabe, versuch mal,
mit dem Gauß-Verfahren in eine rechte obere Dreiecksmatrix umzuformen.
Charly Hey Rike, mit welchem Vielfachen soll ich denn x in der 3. Zeile eliminieren? Mist! Warum sollen denn die Jungs und Mädels nicht auch mal Mehrfache der 3. Zeile zur 1. Zeile addieren?
Rike Klar, Ihr könnt das geschickt umstellen und das Negative der 2. Zeile zur 1. Zeile addieren, dann kriegt Ihr
Charly Hey, das ist die rechte untere Dreiecksmatrix. Ich kann sogar die Lösung im Kopf berechnen:
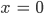
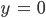
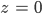
Rike Stimmt. Das könnt Ihr machen, aber es heißt nicht mehr Gauß-Algorithmus, und es ist etwas unsystematisch. Ihr bringt Euch so stark ein und versucht, Lösungen schnell zu finden, ja eigentlich aus der konkreten Struktur Vereinfachungen zu machen, doch das kann man nicht automatisieren, stell Dir doch mal größere Systeme vor. Du nimmst ein System, na 100 x 100, und mittendrin steht eine Zeile nur mit einer Variablen. Dann versuchst Du das aufzulösen, und 99 Gleichungen bleiben. Dann schaust Du, ob Du was vereinfachen kannst ... soll ich Dir mal so ein hübsches System geben?
Charly Rike, lass mal, ist okay, ich will das verstehen und ordentlich machen. Wenn wir Dein System nicht “geschickt” lösen können, dann versagt wohl der gute alte Gauß hier?
Rike Nein, zum Gauß-Verfahren gehört dazu, dass es erlaubt ist, Zeilen zu tauschen. Und das machen wir mal: Die 3. Zeile tauschen wir mit der 1. Zeile:
Charly Okay, dann nehme ich "Gauß" für die 2. zur 3. Zeile:
Und schon sind wir fertig! x = y = z = 0 ist die Lösung.
2. Gegenbeispiel
Rike Jawoll. Doch es gibt noch ein weiteres fundamentales Problem: Nehmen wir mal das Beispiel
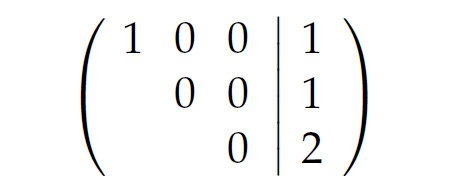
Charly Dann lass mich doch mal den Gauß-Algorithmus testen: Das Negative der 1. Zeile zur 2. und das Negative der 1. Zeile zur 3. ergibt
Wenn ich das jetzt für z löse
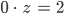
Hmmmm??? Rike, das ist ein blödes Beispiel, wie geht das jetzt weiter? Wenn da Deine kleine Schwester sitzt, und mich dieses (!) Beispiel fragt, was dann? Division durch Null, irgendein Trick?
Rike Haha, kein Trick. Der Gauß-Algorithmus funktioniert nicht für alle linearen Gleichungssysteme.
Charly Echt jetzt? Wieso denn?
Rike Schau mal, Du kannst Dir mein Beispiel

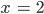
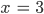
grafisch vorstellen. Das sind 3 Flächen im 3-dimensionalen Raum.
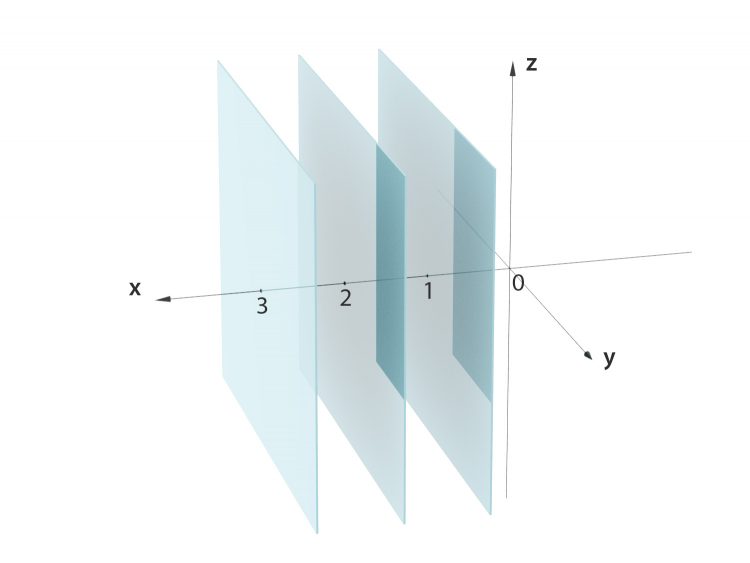
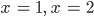
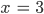
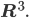
Charly Und die sind parallel. Die haben keinen gemeinsamen Punkt. Okay. Na gut. Wir sind die ersten, die so was merken. Aber wie kann man das feststellen, ob der Algorithmus klappt, wie lautet die Voraussetzung?
Voraussetzung für den Gauß-Algorithmus
Rike Die Voraussetzung für den Gauß-Algorithmus ist, dass die Koeffizientenmatrix regulär ist.
Charly Was heißt das? Du rechnest die Determinante der Koeffizientenmatrix (ohne den rechten Teil) aus, und die muß ungleich Null sein.
Charly Okay, das ist didaktisch etwas schwierig, den Begriff der Determinanten hatte ich bis dahin nicht...
Rike Ihr habt doch nur 2 x 2- oder 3 x 3-Systeme. Da kannst Du die Determinanten konkret als Formel geben:
Ist
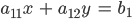
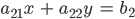
ein lineares Gleichungssystem mit den 2 Unbekannten x und y, dann ist
die Koeffizientenmatrix (ohne rechten Teil). Die Determinante der Koeffizientenmatrix A ist
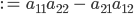
Charly Okay, und für 3 x 3-Systeme?
Rike Wir schreiben
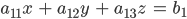
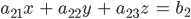
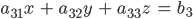
für ein lineares Gleichungssystem mit 3 Unbekannten. Dann ist die Koeffizientenmatrix (wieder ohne den rechten Teil)
und die Determinante der Koeffizientenmatrix A ist
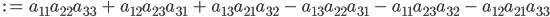
Charly Ooooh! Eine Herausforderung!
Rike Klar, doch da gibt es ein paar Eselsbrücken, das erkläre ich Dir heute Abend. Für beide Systeme gilt: Wenn
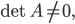
dann liefert der Gauß-Algorithmus eine einzige Lösung.
Zusammenfassung
Der Gauß-Algorithmus besteht darin, das Gleichungssystem in die rechte obere Dreiecksform zu bringen, indem man geeignete Vielfache einer Zeile zu geeigneten Vielfachen einer anderen Zeile darunter addiert ("von oben nach unten") oder Zeilen tauscht, wenn das nicht geht.
Hat man die rechte obere Dreiecksmatrix, so löst man das neue System von "unten nach oben" auf.
Charly Super Rike, ich danke Dir. Warum steht das nicht im Mathebuch? Wieso lässt man mich als Lehrer vor die Wand laufen? Dahinten sehe ich schon Max, dann können wir gleich noch ein Stündchen Beachvolleyball spielen.
Rike Hahaha.
***
Übungsaufgaben
Löse mittels Gauß-Verfahren
Lösungen
- Mit “Gauß” nicht lösbar