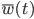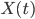Die Feuerwehrfunktion

Rike und Charly haben wieder Matheschulbücher angeschaut. Sie genießen nun den Sonnenschein an der Nordsee während Max wieder seine Strecke (2 x 8 km) am Strand joggt. Als sie das Feuerwehrauto sehen, fällt Charly die unglückliche Feuerwehraufgabe ein. Und die geht so:

Lukas ist Mitglied der freiwilligen Feuerwehr. Das neue Tanklöschfahrzeug enthält einen Wasservorrat von 2000 l. Bei einem Feuerwehreinsatz werden pro Minute 125 l aus dem Tank gepumpt. Lukas überlegt, wie lange der Vorrat reicht.

Rike Welche mathematischen Begriffe und Methoden sollen denn damit eingeführt werden?

Charly Die Funktion.

Rike Und wie geht es weiter?

Schulbuch-Feuerwehrfunktion

Charly Zuerst soll ich eine Wertetabelle aufstellen

Tabelle nach Ch. Berg, J. Brüggemann, B. Heinrich et al.:
Mathematik Technik – Fachoberschulreife, Cornelsen, Berlin, 2015, S. 56.

Dann wird das als Funktion gezeichnet, dabei fehlen irgendwie die Einheiten an der Zeichnung, ungefähr so:

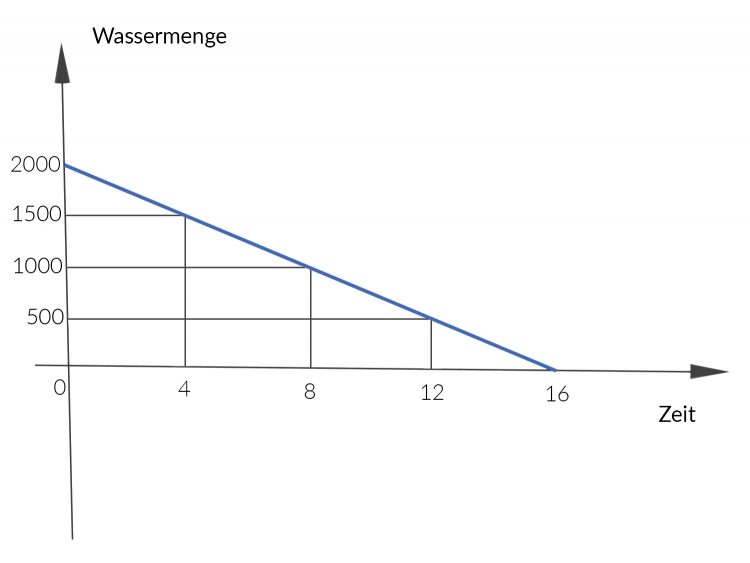
Dann wird aus der Abbildung geschlussfolgert, dass nach 16  S t u n d e n  der Tank leer ist.

Rike Haha, und weiter?

Charly Und schließlich wird der Definitionsbereich der Funktion für den Wasserstand im Tank als Intervall von 0 bis 16

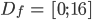
festgelegt.

Rike Oooh! Charly, ich glaube, wir müssen das Buch korrigieren. Da sind mehrere Denkfehler drin.

Charly Okay, was denn?

Rike Charly, gewöhne Dir an, Einheiten bei technischen Aufgaben konsequent zu benutzen, dann wirst Du nicht Stunden und Minuten verwechseln. Und: Techniker nehmen am liebsten die Variable 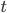für die Zeit.

Charly Na klar.

Diskrete Feuerwehrfunktion

Rike An die Wertetabelle schreibst Du Einheiten dran, dann ist die okay.

Charly Klaro.

Rike Die Zeichnung ist aber falsch! Wir haben die Aussage über die Änderung des Wasserstandes über einen Zeitraum von 1 min! Verstehst Du, wir wissen nichts über den Vorgang im  V e r l a u f  der einen Minute.

Charly Ist das nicht egal? Lass uns doch nur Minuten als kleinste Zeiteinheit betrachten.

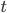
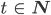
Rike Gut, lass uns das machen. Wir nehmen dann Zeiten , für die nur die natürlichen Zahlen zugelassen sind, also

Charly O, ich sehe schon, jetzt habe ich armer Mathelehrer schon verloren!

Rike Nein, Du hast nicht verloren. Wir nehmen einfach eine digitale, diskrete Uhr, die kennst Du doch.

Charly Klar! Das Handy!

Rike Die Werte für den Wasserstand im Tank würde ich gern mit

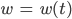
bezeichnen. Wollen wir in ganzen Litern rechnen oder auch in Teilen von Litern?

Charly Bei 125 l/min reichen doch ganze Zahlen.

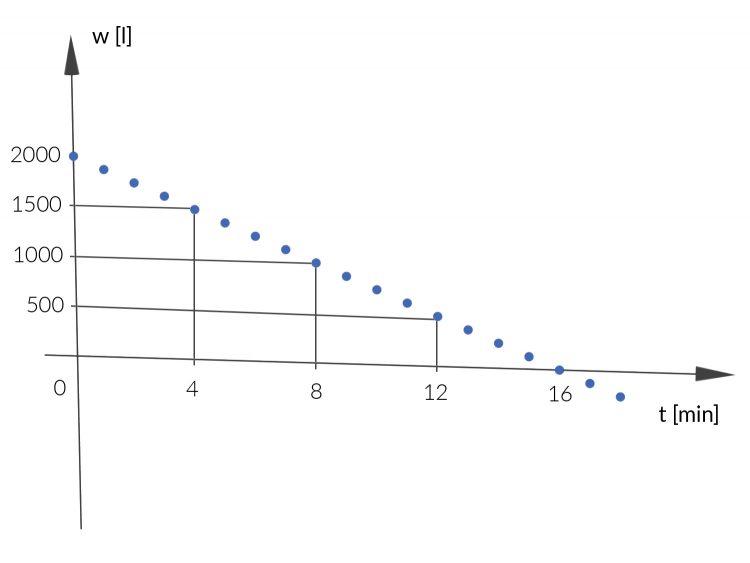
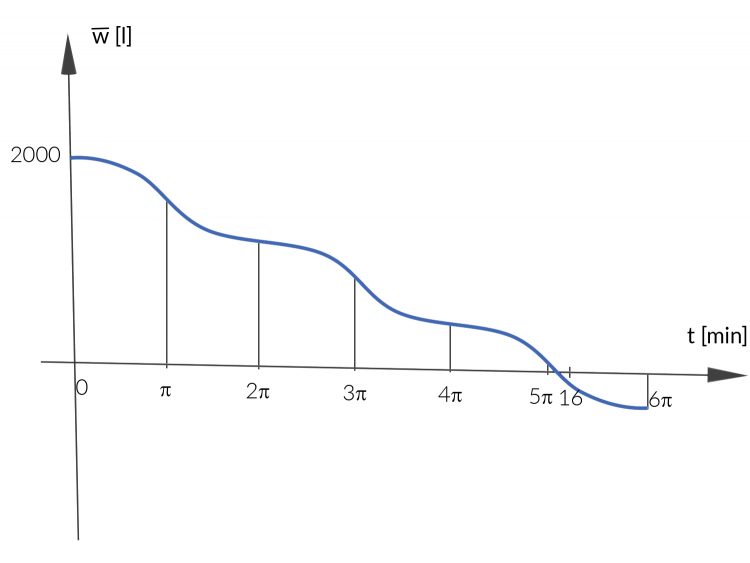
Rike Okay, dann definieren wir die Funktion 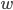als Abbildung von den natürlichen Zahlen in die ganzen Zahlen

Graphisch sieht das so aus:

Und als Formel findest Du leicht

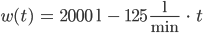
Definitionsbereich und postive Funktionswerte

Charly Alles klar! Und was machen wir mit den negativen Werten für die Wassermengen? Im Buch wurde erst ausgerechnet, wo die Werte positiv bleiben, und danach wurde der Definitionsbereich festgelegt.

Rike Das kriegst Du eine Selbstreferenz! Aus physikalischen Gründen wird eine Formel aufgestellt, die Werte berechnet und dann erst festgelegt, für welche Argumente die Werte berechnet werden dürfen, hmmm … formal sieht das so aus:

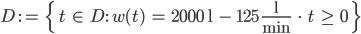
Charly Nö, eine Selbstreferenz muss an der Stelle nicht sein. Aber positive Werte für 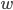will ich auch.

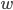
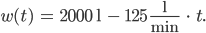
Rike Gut! Das geht standardmäßig so: Wir haben die Funktion wie beschrieben

Das ist ein mathematisches Modell. Für die Feuerwehr  i n t e r p r e t i e r e n  wir nur Werte

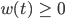
Charly Okay, Du hast recht, die Lehrbuchlehrer wollen immer so anschaulich sein, aber korrekt ist es, wenn wir Mathematik machen und nicht mit der Feuerwehr argumentieren.

Rike Ja, das war jetzt ein bisschen weltanschaulich. Aber was ist, wenn bei Dir im Unterricht ein Schüler sitzt, der bei der Feuerwehr ist, und der sagt Dir dann, dass 16 min sehr kurz sind, und dass da vielleicht Sekunden über Leben und Tod entscheiden.

Charly Mist!

Zufällige Feuerwehraufgabe

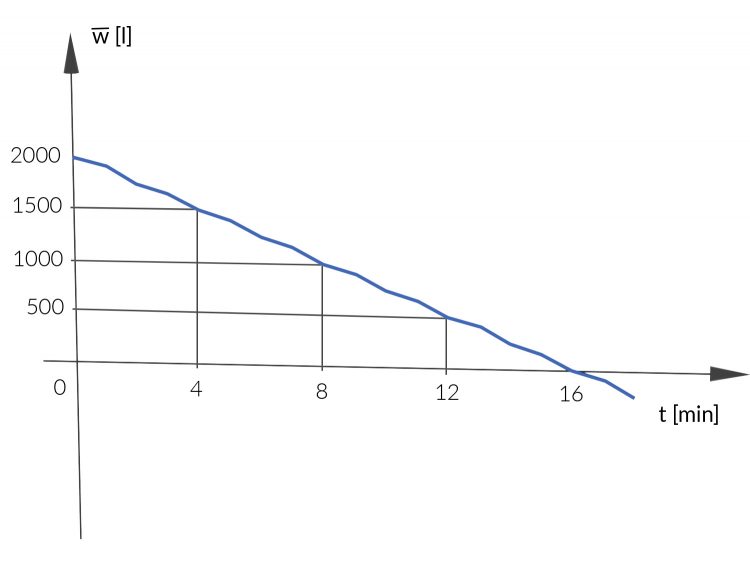
Rike Dann könnten wir ein stetiges Modell rechnen, wo Du jede noch so kleine Zeiteinheit betrachten kannst.

Charly Gut!

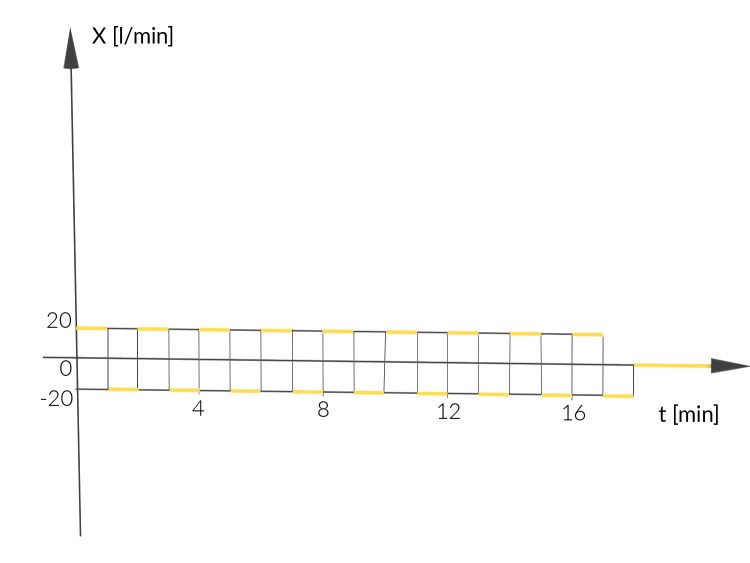
Rike Wir finden jetzt eine neue Funktion

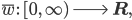
deren Berechnungsvorschrift wir erst noch aus den beiden Bedingungen herleiten:

1. Die Änderung der Wassermenge pro Minute ist

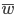
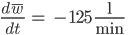
   im Mittel.

2. Du hast einen Anfangswert

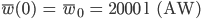
   nahezu sicher.

Charly Haben wir schon wieder Differenzialgleichungen? Und dazu noch den Zufall?

Rike Klar, Evolutionsprozesse lassen sich sehr gut mit Dgln. beschreiben, und Du bist vielleicht der erste Lehrer, der das den Berufsschülern beibringt.

Charly Na super!

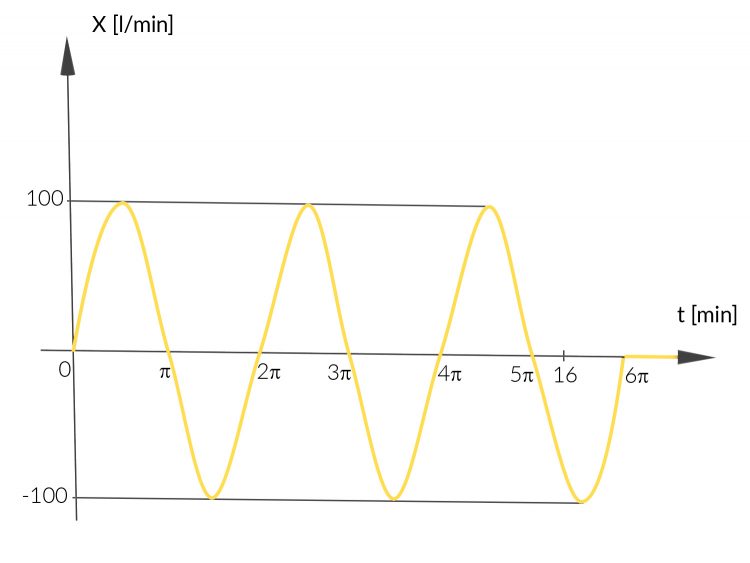
Rike Ist nicht schwer. Die erste Bedingung schreiben wir als

ist eine Funktion mit zufälligen Werten oder einfach eine weitere Funktion, die die Störung des Gleichmaßes beschreibt:

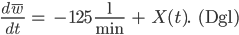
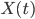
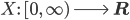
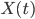
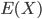
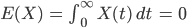
Das können wir dann gut physikalisch interpretieren, da die Pumpe nicht ganz regelmäßig spritzt. Sie fördert nur  i m  M i t t e l  125 l/min. muss im Mittel Null sein, also ihr Erwartungswert muss Null sein. Das schreibt sich so

Charly Na gut.

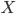
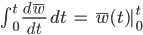
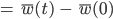
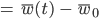
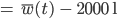
Rike Dann können wir diese Anfangswertaufgabe (Dgl + AW) mit dem Zufall integrieren, zuerst die linke Seite:

Und dann die rechte Seite:

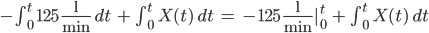
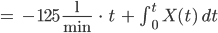
Charly Und jetzt linke und rechte Seite gleichsetzen? Lass mich mal!

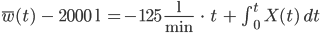
Dann kriege ich gut 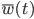, nämlich

Die beste Feuerwehrfunktion

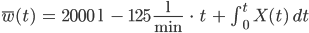
Rike Stimmt.

Charly Hey! Das ist die beste Feuerwehrfunktion!

***

Übungsaufgaben

Zeichne für verschiedene

1. 
2. 
3. Finde selbst eine Funktion

Lösungen