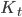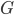Horizont als Zufallsweg II

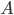
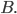
Im Beitrag Horizont als Zufallsweg haben wir geometrische und topologische Eigenschaften der Horizontkurve untersucht. Der Horizont wurde als Weg vom linken zum rechten Bildrand verstanden. Fotografische Eigenschaften (wie Fokus, Auflösung und Objektiv) wirken sich auf die Glattheit der Kurve aus. Alle Beispiele hatten einen zusammenhängenden Weg von nach Dieser Weg kann sich möglicherweise selbst berühren.

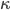
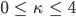
Lassen Sie uns auch jetzt nur Landschaftsfotos betrachten, die einen Horizont in diesem Sinne haben. Bei Verdeckungen wählen wir den oberen Weg. Aufgrund dieser Konstruktion haben wir Wege, die sich als Brownsche Bewegungen auffassen lassen. Diese wurden mittels ihrer Geschwindigkeit klassifiziert. In unseren Beispielen bekommen wir immer die Klasse von Wegen, die zu

gehört. Das sind solche, die sich niemals selbst schneiden. Zum Beispiel hat dieser Baum die folgende Horizontlinie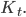

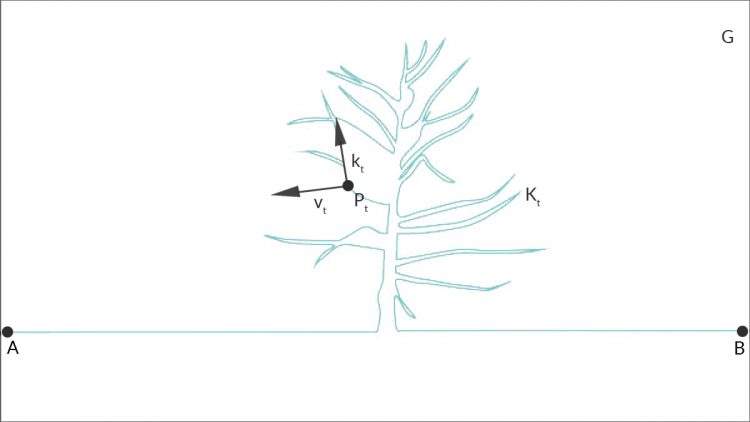
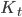
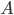
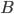
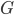
Betrachten wir nun statt statischer Fotos bewegte Landschaften – zum Beispiel mit einem vom Wind bewegten Baum.

Sei

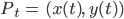
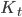
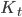
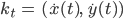
ein Punkt auf der bewegten Geometrie auf der Horizontlinie ; sei wieder die Horizontlinie und

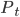
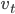
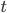
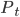
sei der Geschwindigkeitsvektor für jeden Punkt . Sei ferner der Geschwindigkeitsvektor für den Wind, der zur Zeit an angreift.

Dabei können wir folgende Phänomene finden:

Einfache Linie von A nach B

Für

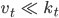
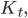
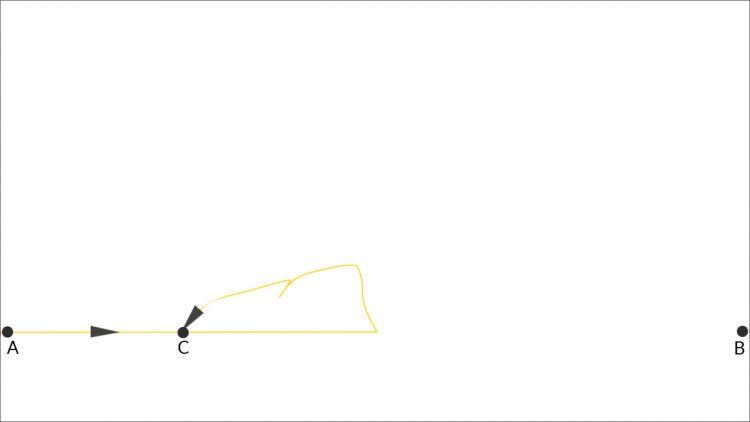
haben wir eine stetige Korrektur der ursprünglichen Kurve die weiterhin dieselben geometrischen und topologischen Eigenschaften hat.

Sich selbst schneidende Linie von A nach B

Für

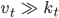
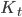
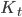
können wir eine sich selbst schneidende Kurve erhalten.

Geschlossene Linie

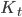
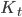
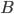
Bei umknickenden Bäumen können sogar geschlossene Linien auftreten. Geschlossen meint hier, dass der Endpunkt der Linie wieder auf dem Horizont liegt und dass diese Linie nicht zu führt.

verlässt G

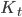
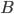
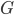
Bei abrechenden Ästen können Linien auftreten, die den Punkt nicht erreichen und das Gebiet verlassen.

Fazit

1. Wie schon in der Theorie der Stochastischen Loewner Evolution (SLE) von Rohde und Schramm – die ja für mikroskopische zufällige Prozesse entstand – finden wir auch in makroskopischen Modellen zufällige Erscheinungen, die sich ebenso klassifizieren lassen. Hier haben wir durch die Horizontlinie, auf der man mit einer Geschwindigkeit auf einer fotografischen Projektion einer Geometrie entlanggeht und die einer äußeren Kraft unterliegt – genau wie bei der SLE – einen großen Einfluss der Geschwindigkeiten (dort: ).
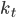
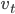
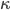
2. Außerdem haben wir durch die äußere Kraft erstmals in unserem Modell sich selbst schneidende Linien, was  bei der SLE einem

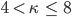
   entspricht.

3. Im Gegensatz zur SLE, wo bei größeren Geschwindigkeiten komplexere Kurven entstehen, bekommen wir solche in Landschaftsfotos uns für langsamere Geschwindigkeiten und größere Geschwindigkeiten der äußeren Kraft.

***

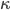
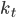
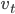
Übungsaufgabe

Gibt es Konstellationen, in denen auch der 3. Fall eintritt, sodass die Fläche ausfüllt?