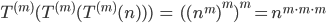Charly hat gerade Beachvolleyball mit Jugendlichen gespielt. Die sind an der Nordsee zur Kur wegen ihrer Essstörungen. Charly erzählt, dass einige zu viel Sport machen, nur um abzunehmen, und andere, die Übergewichtigen, möchten keinen Sport machen.
Methodik im Sport
Rike Charly, sag mal, geht das, kannst Du mit allen gemeinsam Volleyball spielen?
Charly Klar, ich habe doch im Sportstudium Motivation gelernt. Ich erkläre ein paar Regeln über den Umgang mit dem Ball und wir fangen vorsichtig mit ein paar Übungen paarweise und ganz locker an. Dann kommen die Regeln über gesundes Bewegen, Pausen, Essen und Trinken beim Sport und erst dann die Regeln des eigentlichen Spiels. Aber weißt Du, sie wollen das gar nicht hören.
Rike Und wie gehst Du damit um?
Charly Wir machen ein paar Übungen, bis wir dahin kommen, dass es ohne Regeln nicht gut weitergeht.
Rike Okay, Charly.
Charly Dann versuche ich sie zu motivieren, dass wir weiterspielen und außerdem versuche ich, dass sich alle gut dabei fühlen.
Rike Das hört sich toll an.
Charly Jetzt frage ich mich, ob das nicht auch in Mathe funktionieren kann. Wenn zum Beispiel für Kinder der 7. Klasse oder Erwachsene auf dem 2. Bildungsweg Rechnen mit einer Veränderlichen, lineare und quadratische Funktionen, Umformen von Termen, Ungleichungen – eben der ganze Schulalgebra-Kram auf dem Programm steht. Hier habe ich ein Buch, das fängt mit unklaren Regeln an und bringt die Begriffe nicht auf den Punkt. So wird der Begriff der Variablen oder des Terms nicht gut erklärt, eigentlich ist der Teil nicht folgerichtig aufgebaut und nicht zu gebrauchen.
Rike Wenn der Begriff Term unklar bleibt, dann kannst Du Terme ja auch nicht richtig umformen.
"Schulalgebra-Definitionen"
Charly Hier steht:
Variablen sind Platzhalter für beliebige Zahlen. Anstelle einer Variablen kann immer eine konkrete Zahl geschrieben werden.
Ein Term ist ein Rechenausdruck zur Berechnung eines Wertes. Er kann Zahlen, Rechenzeichen, Klammern und Variablen enthalten.
Ist 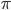
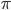

Rike Es ist wirklich nicht gut, den Term-Begriff als "Rechenausdruck zur Berechnung eines Wertes, der Zahlen, Rechenzeichen, Klammern und Variablen enthalten kann" festzulegen. Eine umgangsprachliche Erläuterung ist doch keine Definition!
Charly Stimmt.
Kommutativgesetz
Rike Die meisten Umformungen gehen auf das Kommutativgesetz
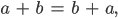
Assoziativgesetz
das Assoziativgesetz
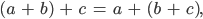
Distributivgesetz
und das Distributivgesetz
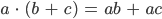
für verschiedene Zahlräume zurück, natürlich brauchst Du auch die Subtraktion, wenn Du
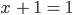
lösen willst oder die Division zur Lösung von
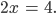
Charly Stimmt. Das steht alles in den höheren Algebra-Büchern. Aber was ist ein korrekter Term?
Rike Lass es uns wie bei Deinem Sport machen. Wir bauen alles folgerichtig auf. Wie weit kommst Du in der ersten Übungseinheit?
Charly Nicht weit.
Rike Wie lange brauchst Du, bis alle Deine Schüler Volleyball spielen und Ihr ein paar richtige Spiele mit ein bisschen Wettkampfgeist macht?
Charly 4 Wochen?
Rike Na, siehst Du. Vielleicht fangen wir mit den natürlichen Zahlen an? Und Du denkst Dir motivierende, witzige Wohlfühlaufgaben aus?
Charly Okay.
Nachfolger einer Zahl
Rike Wir machen das wie Wladimir Wojewodski. Wir nehmen das Nichts, also die Null:
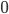
Und finden dazu die 1 als ihren Nachfolger succ (successor):
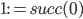
Charly Prima!
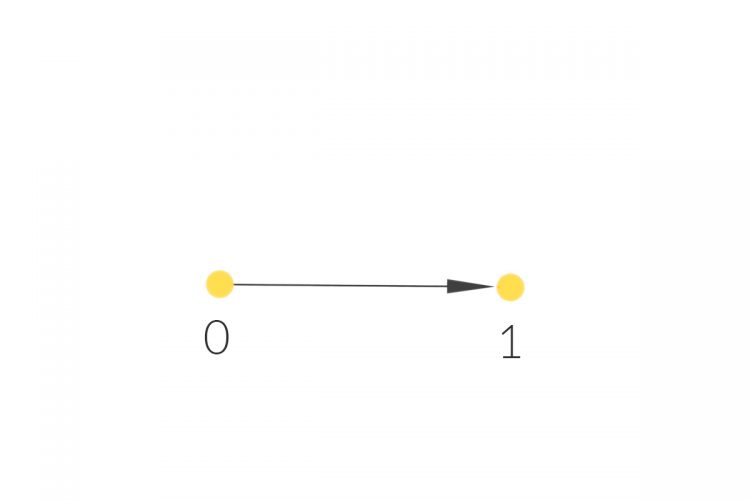
Rike Und der Nachfolger der 1 ist die Zwei:
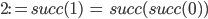
Charly Okay, sehr gut, da habe ich schon eine Wohlfühlaufgabe!
Rike So erhälst Du alle natürlichen Zahlen
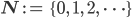
Dieses
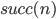
kannst Du auch schreiben als
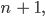
also dieses Nachfolgersein ist praktisch die Addition mit 1:
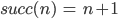
Charly Okay
Syntax elementarer Terme in N
Rike So kannst Du die Addition mit 1 als ersten elementaren und korrekten Term in 
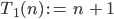
Selbstverständlich gilt das Kommutativgesetz und es ist
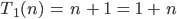
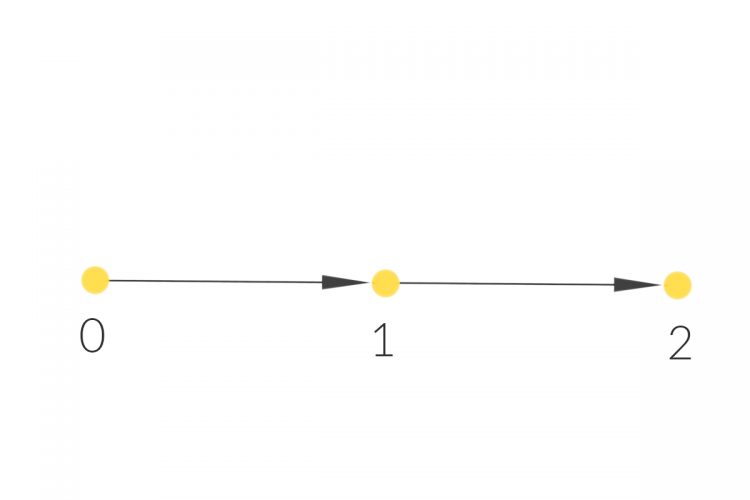
Charly Gut, jetzt könnnen wir ein bisschen schneller machen und
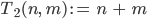
als m-fachen Nachfolger von 
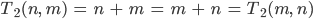
Rike Ja gut, jetzt brauchen wir nur noch die Multiplikation natürlicher Zahlen, dazu kannst Du
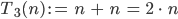
erklären und analog
Hierzu brauchst Du das Assoziativgesetz:
Charly Gut. So sind 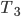
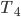
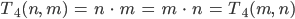
Rike Ja, jetzt kommt das Distributivgesetz: Du erlaubst, Addition und Multiplikation in einem neuen korrekten Term und mit erlaubten Umformungen:
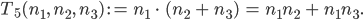
Charly Ich verstehe, schätze, jetzt kommen die Potenzgesetze
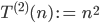
ist ein korrekter elementarer Term und
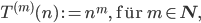
ebenfalls?
Rike Gut, jetzt haben wir die elementaren Rechenoperationen und ihre Verknüpfungen durch Assoziativ- und Distributivgesetz und dazu elementare korrekte Terme.
Charly Gut. Und weiter?
Syntax höherer Terme
Rike Jetzt lässt Du statt der Variablen 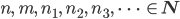
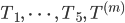
Charly Warte mal, dann kann ich für alle 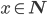
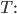
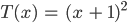
als Potenz von 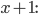
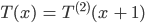
und
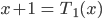
als Summe schreiben, zusammen gibt das
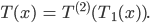
Rike Ja, das ist dann ein korrekter Term 2. Ordnung. Und gleichzeitig ist die Berechnung klar: Die 2er-Potenz ist ein Produkt:
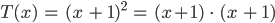
Jetzt nimmst Du das Distributivgesetz für den ersten Faktor:
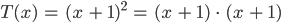
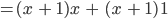
Und jetzt nochmal das Distributivgesetz:
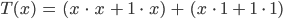
Charly Klar,
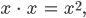
dann nehme ich das Assoziativgesetz und kriege
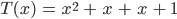
und mit
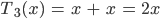
habe ich
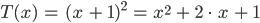
Rike Toll.
Charly Rike, das ist toll, so kann ich alle korrekten Terme durch Ineinandereinsetzen erklären und auch berechnen. Dann brauche ich nicht den unglücklichen Begriff äquivalente Terme, der beim zulässigen (?) Einsetzen von Zahlen und Aufstellen von Wertetabellen(!) den gleichen Wert ergeben soll.
Und für diese Aufgabe hier im Buch, schau mal:
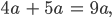
die ich ja mit dem Distributivgesetz löse:
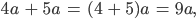
brauche ich nicht den Begriff der gleichartigen Terme.
Rike Nein, den braucht keiner.
Charly Was meinst Du, sollen wir unendlich viele Einsetzungen
zulassen?
Rike Hahaha.
Übungsaufgaben
- Ist es sinnvoll, unendlich viele Einsetzungen zuzulassen?
- Ist
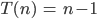
ein korrekter Term?
- Ist
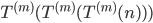
ein korrekter Term? Wie kann er berechnet werden?
Lösungen
- nein
- nein
- ja