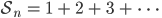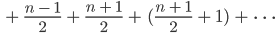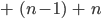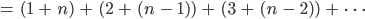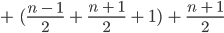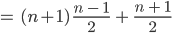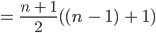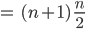Charly Diese vielen Wellen erinnern mich an eine Aufgabe über natürliche Zahlen. Du glaubst es nicht, für Hauptschüler in der 9. Klasse!
Max Was denn?
Charly Die Jungs und Mädels sollen beweisen, dass für jede Zahl 
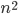

Max Ehrlich?
Die Aufgabe
Charly Naja, es wird noch genauer ausgeführt. Formal heißt die Aufgabe:
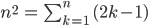
Max Sieht echt kompliziert aus. Sowas hatte ich nicht, warte mal, aber für

kriege ich
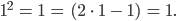
Stimmt! Und für 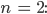
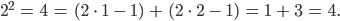
Vollständige Induktion
Stimmt! Rike hatte mir vor langer Zeit die natürlichen Zahlen erklärt, sie hat gesagt, das Wesen der natürlichen Zahlen ist, dass man eine erste hat, zum Beispiel die 1,
und wenn man dann zu irgendeiner natürlichen Zahl 
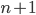
Charly Das ist die vollständige Induktion!
Max Hmm.
Charly Das ist wie heute bei stürmischem Meer. Du hast hier vorn eine Welle.
Max Klar!
Charly Und wenn Du nun irgendeine Welle anschaust, und wenn Du für diese Welle einen Nachfolger findest, dann hast Du so viele Wellen wie natürliche Zahlen.
Max Klar! Jede Welle hat einen Nachfolger, einmal um die Welt herum und immer weiter…
Charly Hahaha. Weißt Du, das nehmen wir als Beweisprinzip. Du hast gerade überprüft, dass die Behauptung für

richtig ist. Jetzt starten wir mit irgendeinem 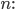
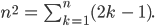
Wenn wir nun zeigen können, dass das auch für 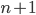
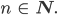
Max Okay.
Charly Schau mal, wir berechnen einfach die Summe 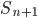
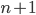
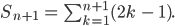
Wir schreiben das geschickter als Summe von 
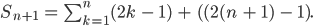
Der erste Summand ist 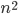
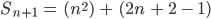
Max Hey, das ist ja easy!
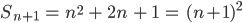
Charly Fertig!
Max Ist das mit der vollständigen Induktion nicht ein bisschen zu abstrakt für die Hauptschüler, 9. Klasse? Willst Du nicht einfach ein paar Zahlen 
Die gaußsche Anekdote
Charly Du, da fällt mir die Anekdote von Gauß ein. Als Gauß 9-jährig in die „Rechenklasse“ seiner Schule versetzt wurde, in eine Klasse, wo mehrere Jahrgänge gleichzeitig unterrichtet wurden, manche Schüler bis zum 15. Lebensjahr, hat der Lehrer – gerade in Gauß‘ erster Rechenstunde – die Aufgabe aufgegeben, die ersten, sagen wir mal 100 Zahlen zu addieren. Der Lehrer ist mit der „Karwatsche“ auf und ab gegangen zwischen den etwa 100 Schülern. Gauß hatte die Lösung zuerst. Er musste sie auf eine Tafel schreiben und nach vorne bringen. Er hat nur „5050“ hingeschrieben und hat das durch geschickte Addition der 1. und letzten Zahl (1+100=101) und so weiter (2+99=101, …) das bis 50+51=101, also
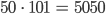
im Kopf gelöst. Die anderen haben gerechnet und gerechnet und ihre Tafel viel später nach ihm hingelegt. Gauß hatte recht, und nur wenige mit ihm; die mit der falschen Lösung wurden mit der Karwatsche „rectificirt“, so hieß das damals.
Max Steht das auch in diesem Mathebuch?
Charly Nein!
Max Das gehört da rein! Ist doch eine schöne Geschichte. Du hast recht, Mathematik ist nicht Addition von Zahlen, immer wieder, und mit der Karwatsche daneben stehen…
Die gaußsche Summenformel
Charly Vielleicht entwerfe ich ein Arbeitsblatt mit dieser Geschichte, der geschickten Addition und vollständiger Induktion. Du kannst die Aufgabe der Addition der ersten 
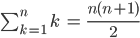
Max Okay.
Charly Wenn Du das Ergebnis kennst, kannst Du die Summe der ersten 
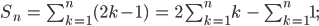
das ist nämlich das Distributivgesetz. Die erste Summe ist nun die gaußsche Summenformel von 1 bis 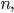
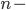
Max Okay, die erste Summe ergibt 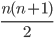
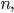
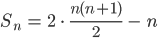
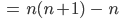
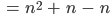
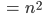
Charly Hey! Stimmt. Am liebsten würde ich in mein Arbeitsblatt als Abschluss schreiben, dass Mathematik sehr wenig mit Rechnen zu tun hat, sehr viel mit Knobeln und systematischem Nachdenken, das habe ich kürzlich in einem Blog gelesen, man muss geduldig sein.
Max Wie beim Sport?
Charly Wie beim Sport! Es kann einem passieren, dass man monatelang über ein Problem nachdenkt und am Ende gar nichts herausbekommt.
Max Hahaha.
***
Übungsaufgaben
- Zeige die gaußsche Summenformel mittels vollständiger Induktion!
- Zeige die gaußsche Summenformel durch geschickte Addition!
Lösungen
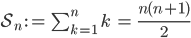
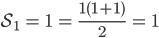
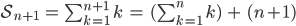
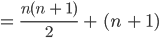
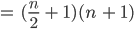
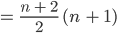
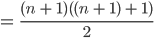
- Fall

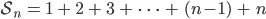
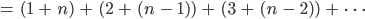
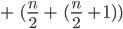
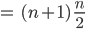
Fall