Charly Gleich müssen wir eine Halse machen. Jetzt fahren wir mit dem Wind.
Max Okay, Du sagst es an.
Charly Jetzt!
Max Okayyyy!
Charly Super! Jetzt haben wir den Wind von links hinten.
Du, Max, ich habe mich gestern Abend weiter auf den Mathe-Unterricht vorbereitet; ich schätze, wenn der Autor dieses Mathebuches dabei wäre, dann würde er sagen: Jetzt haben wir den entgegengesetzten Wind, das sind die negativen ganzen Zahlen, jetzt können wir subtrahieren, zum Beispiel
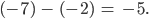
Lasst uns nun mit den rationalen Zahlen weitermachen!
Max Das kapiert doch kein Mensch! So kannst Du das nicht machen!
Charly Tatsächlich bilden die natürlichen Zahlen den nichtnegativen Teil der ganzen Zahlen, dann gibt es etwas Motivation in Form von negativen Temperaturen oder Schulden bei der Bank, und fertig sind die negativen ganzen Zahlen. Diese negativen ganzen Zahlen werden zu 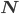
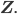
Max Rike würde sich ziemlich aufregen über so unklare Definitionen. Und was machst Du? Wie definierst Du negative Zahlen?
Wojewodskis Zugang zu den ganzen Zahlen
Charly Ach, weißt Du Max, ich habe in dem Buch von Wladimir Wojewodski weitergelesen, womit Rike uns die natürlichen Zahlen erklärt hat, und da habe ich eine tolle Idee gefunden!
Max Dann erklär‘s mir mal, ich bin einfach mal Dein Schüler!
Charly Gut. Also wir sind mit der Null gestartet und haben die 1 als Nachfolger zur Null erklärt. Dann dazu den Nachfolger usw. Schließlich die Addition und Multiplikation in
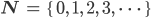
Max Klar, ist doch easy!
Charly Jetzt nehmen wir ein Paar natürlicher Zahlen
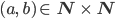
und erklären für solche Paare eine Äquivalenzrelation:
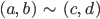
(a, b) und (c,d) sind äquivalent, wenn
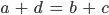
ist.
Max Hmmm.
Charly Hol doch mal a und b auf eine Seite!
Max Okay: Die beiden Paare sind äquivalent, wenn
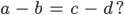
Charly Stimmt! (a, b) und (c, d) sind äquivalent, wenn sie dieselbe Differenz bilden. Und das wurde ohne das Minuszeichen erklärt, nur durch Addition!!!
Ganze nichtnegative Zahlen
Max Cool! Hast Du mal ein Beispiel für mich?
Charly Klar! Lass uns mal (7, 5) nehmen.
Max Okay,
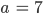
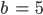
Jetzt finde ich c und d in 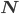
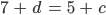
Naja, für
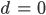
kriege ich
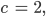
für


usw.
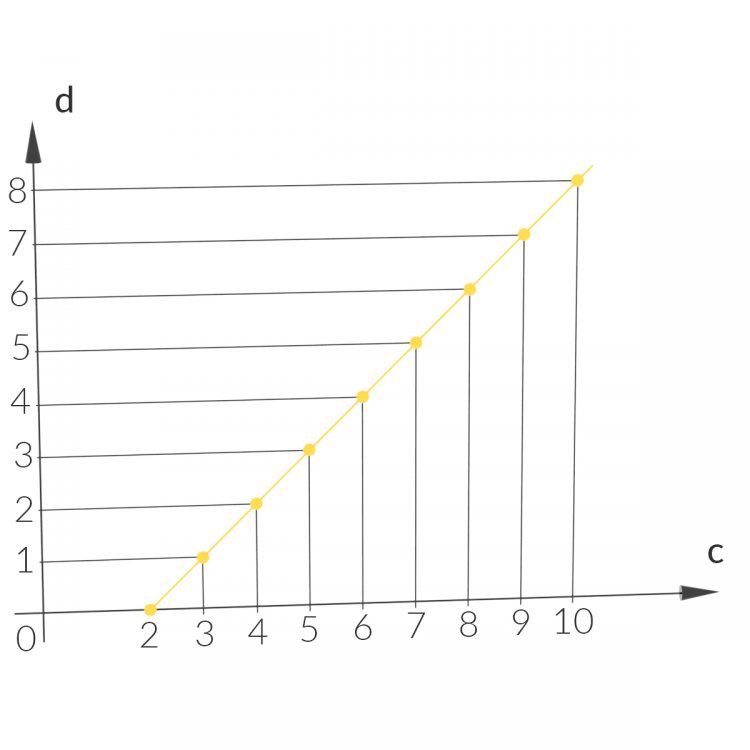
Charly Richtig.

Max Sag mal, sind das unendlich viele Lösungen (c, d)?
Charly Ja, stimmt, und alle die Paare mit der Differenz 2 fassen wir zu einer neuen ganzen Zahl zusammen, und nennen die einfach 2, allgemein geht das so: Ist 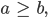
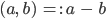
die ganze Zahl n, die auch natürlich ist:
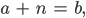
also
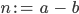
Ganze negative Zahlen
Max Klar, verstehe. Und wenn 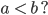
Charly Lass uns mit einem Beispiel beginnen:

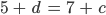
Max Okay, d = 0 und d = 1 geht jetzt nicht, aber für
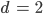
kriege ich
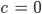
usw.
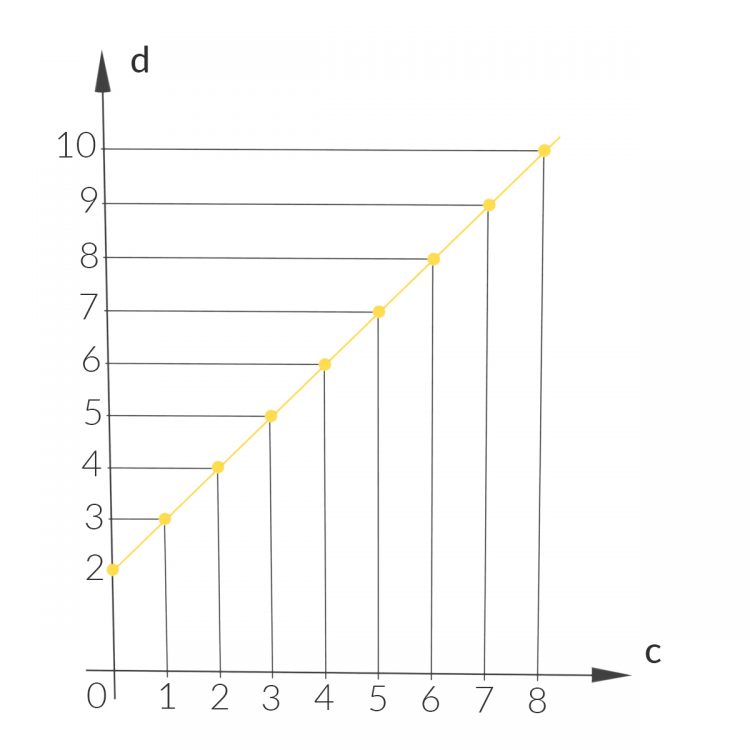
Charly Stimmt. Wir haben unendlich viele Zahlenpaare, die zu (5, 7) äquivalent sind, und das Paar mit
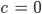
ist (0, 2), also

Max Und das ist dann die negative Zwei?
Charly Richtig, allgemein geht das so: Ist 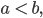
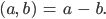
Finden wir das äquivalente Paar (0, n):
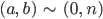
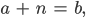
und schreiben für
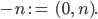
-n ist dann eine negative ganze Zahl.
Max Eigentlich steht -n für unendlich viele Additionsaufgaben.
Charly Richtig, es ist eine Äquivalenzklasse.
Addition, Subtraktion und Multiplikation ganzer Zahlen
Max Aber wie addiert, subtrahiert oder multipliziert man mit solchen Äquivalenzklassen?
Charly Ach, das ist nicht schwer, ich erkläre den Jungs und Mädels den Betrag und das Vorzeichen einer solchen Äquivalenzklasse und dann muss man ein paar Fallunterscheidungen machen.
Max Meinst Du, dass das Deine Klasse versteht?
Charly Na klar, um
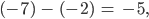
zu berechnen, rechne ich
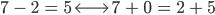
Und weil 7 > 2 nehme ich das Vorzeichen von 7 und kriege
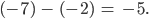
Max Stimmt, das versteh ich. Wollen wir jetzt mal eine Wende machen?
***
Übungsaufgabe
Finde geeignete Definitionen für den Betrag einer ganzen Zahl (a, b) und für das Vorzeichen von (a, b)!
