Reelle Zahlen

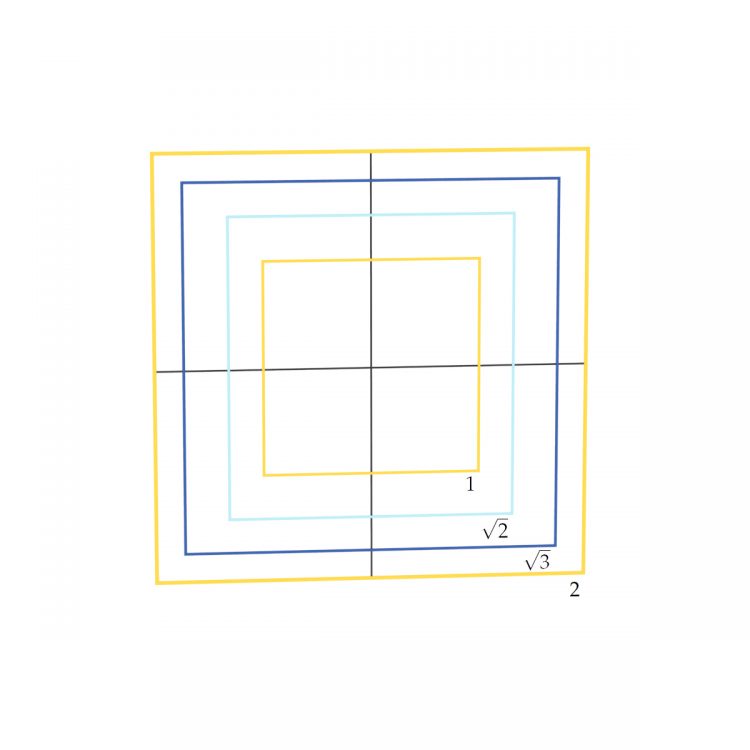
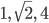Rike, Max und Charly sitzen am Meer am Lagerfeuer. Es ist ihr letzter gemeinsamer Abend. Charly will unbedingt Mathe/Sportlehrer werden und vielleicht klappt es ja mit einer Stelle in NRW. Er hat sich in einem Mathebuch die Einführung der reellen Zahlen angeschaut und will es unbedingt besser machen. Rike erklärt ihm die Primfaktorzerlegung, ein wichtiges Argument, warum nicht alle reellen Zahlen als Bruch dargestellt werden können.

Charly Sag mal, Rike, kannst Du mir erklären, warum 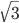nicht rational ist? Ich habe hier ein Buch darüber und verstehe die Argumentation nicht.

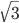
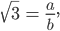
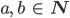
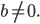
Rike Ach, das ist doch gar nicht schwer. Dahinter steckt die Primfaktorzerlegung. Also, nehmen wir an, ist rational:

teilerfremd,

Charly Klar.

Rike Das schreibst Du als Produkt:

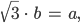
quadrierst es nun

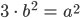
und nennst diese Zahl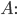

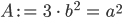
Primfaktorzerlegung

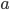
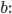
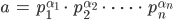
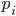
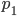
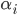
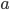
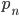
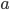
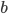
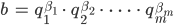
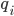
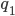
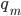
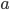
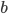
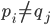
Jetzt nimmst Du die Primfaktorzerlegung von und

sind verschiedene Primzahlen, der Größe nach geordnet, ist die kleinste, sind die Exponenten, mit denen sie in vorkommen, ist die in größte vorkommende Primzahl. Und für machen wir das ebenso:

sind Primzahlen, die kleinste, die größte. Weil und teilerfremd sind, sind alle

Max Rike, mach doch mal ein Beispiel!

Rike Gut,

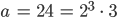
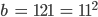
Max Okay.

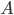
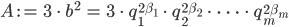
Rike Diese Zerlegung setze ich bei ein:

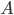
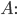
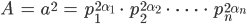
Weil 3 Primzahl ist, ist das eine Zerlegung von in Primfaktoren. Die 3 hat dann einen ungeraden Exponenten. Mit der rechten Seite bekomme ich für

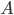
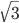
Das heißt, ich habe für zwei verschiedene Primfaktorzerlegungen. Das ist ein Widerspruch zur Eindeutigkeit der Primfaktorzerlegung! Deshalb ist irrational!

Max Okay, verstehe. Aber wieso die Eindeutigkeit der Primfaktorzerlegung?

Der gaußsche Beweis

Rike Jede natürliche Zahl lässt sich eindeutig in Primfaktoren zerlegen. Der Beweis geht indirekt und stammt von Gauß. Er ist über 100 Jahre alt. Nehmen wir an

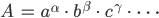
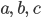
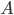
und sind ungleiche Primfaktoren. Wenn sich nun auch anders zerlegen lässt, dann können nur andere Exponenten auftreten, denn es lässt sich immer entscheiden, ob eine Zahl durch eine Primzahl teilbar ist oder nicht.

Charly Stimmt.

Rike Also, eine weitere Zerlegung wäre dann

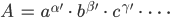
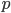
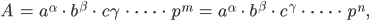
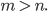
Nehmen wir nun an, dass ein Primfaktor in einer Zerlegung öfter vorkommt als in einer anderen:

Dann erhält man für die Zahl

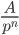
zwei Zerlegungen:

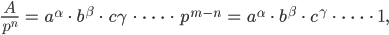
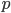
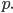
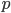
eine mit dem Faktor und eine ohne Das ist ein Widerspruch zu unserer Annahme, jeder Primfaktor kommt entweder in einer Zahl vor oder nicht.

Indirekte Beweise

Max Ist das nicht etwas umständlich? Du nimmst an, dass es verschiedene Zerlegungen gibt, und dann „leitest“ Du her, dass das nicht stimmt.

Charly Ja, Max hat recht, Du hast jetzt zweimal den indirekten Beweis benutzt. Dem liegt die boolsche Logik zugrunde.

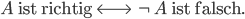
Rike Ja, das ist das Prinzip des ausgeschlossenen Dritten.

Charly Das müsste ich natürlich auch mit den Schülern besprechen. Das fehlt im Buch. Aber sag mal, muss denn die boolsche Logik unbedingt sein?

Rike Du stellst die ganze Elementarmathematik in Frage!

Charly Hey Rike, war doch nicht bös‘ gemeint, ich denke drüber nach, wie ich damit umgehe.

Rike Sag mir Bescheid, wie die Schüler damit klarkommen.

Charly Mache ich.

Fazit über Matheschulbücher

Max Sag mal Charly, jetzt hast Du Mathebücher von der 7. Klasse bis zum Fachabi studiert…

Charly … und eins über Algebra!

Rike Ich habe mir im Winter auch welche mit Prozentrechnung angesehen.

Max … und manchmal waren die Aufgaben so unglücklich formuliert, dass man hohe Mathematik braucht, manchmal hatten die ins Thema einführenden Aufgaben nicht das nötige theoretische Rüstzeug und manchmal war das theoretische Rüstzeug zwar „kindgerecht“ aber mathematisch inkorrekt.

Charly Stimmt! Was fange ich mit Schulbüchern an, die ich als Lehrer inhaltlich nicht akzeptiere und die nicht motivierend sind?

Max Willst Du was Eigenes machen?

Charly Das muss ich wohl.

Rike Ich helfe Dir dabei.

Max Ich auch!

Charly Lasst uns noch ein bisschen feiern heute Abend.

***

Übungsaufgaben

1. Überprüfe die Behauptung

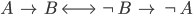
2. Sind rationale Zahlen?