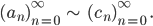Rike Schade, dass die Nordseezeit vorbei ist.
Max Ja, schade, aber ich muss dringend nach Hause, noch ein paar Vorlesungen hören und dann meine letzten Prüfungen machen.
Rike Stimmt, ich muss auch mein Projekt beenden. War doch schön, vor allem mit Charly. Wir haben fast das gesamte Zahlensystem besprochen.
Max Ja, Charly ist ziemlich fit und 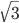
Irrationale Zahlen
Rike Stimmt, eigentlich habe ich nur gezeigt, dass 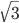
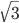
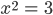
Max Stimmt, weiß ich schon.
Rike Alle solche algebraische Zahlen plus die rationalen Zahlen 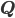
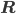
Max Ja, ich weiß, 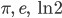
Rike Richtig. Doch es gibt noch andere Zugänge.
Max Ja?
Reelle Zahlen als Äquivalenzklassen
Rike Ja! Zum Beispiel könnte man alle konvergenten Folgen 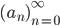
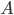
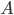
Max Was meinst Du genau?
Rike Alle Folgen 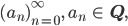
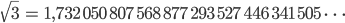
annähern, identifizieren wir mit 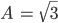
Max Okay.
Definition der Äquivalenzrelation
Rike Dazu muss man eine Äquivalenzrelation einführen:
Zwei Folgen 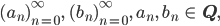

genau dann, wenn
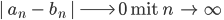
Dann identifizieren wir alle solche äquivalenten 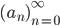
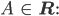
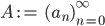
Weil für 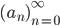
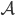
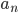
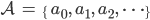
betrachten. Das ist eine Teilmenge der rationalen Zahlen.
Max Okay. Hast Du mir nicht neulich im Schwimmbad die Kontinuumshypothese erklärt und gesagt, dass die Menge der Teilmengen in 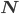
Rike Stimmt! Das ist hier ebenso, die Menge aller Teilmengen in 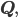
Max Okay.
Die Kardinalzahl für das Kontinuum
Rike Aber nun frage ich mich, warum sollten die reellen Zahlen – also alle rationalen Zahlen plus ihre Grenzwerte – das Kontinuum bilden?
Max Hmm, liegen die nicht alle auf dem Zahlenstrahl?
Rike Richtig, das ist unsere Vorstellung von 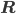
Max Okay.
Rike Ja, man kann die reellen Zahlen auch axiomatisch einführen, ohne eine einzige Zahl dabei zu nennen oder zu benutzen.
Max Oh Mann! Nicht sehr anschaulich!
Rike Andere führen den Zahlenstrahl nur für rationale Zahlen ein.
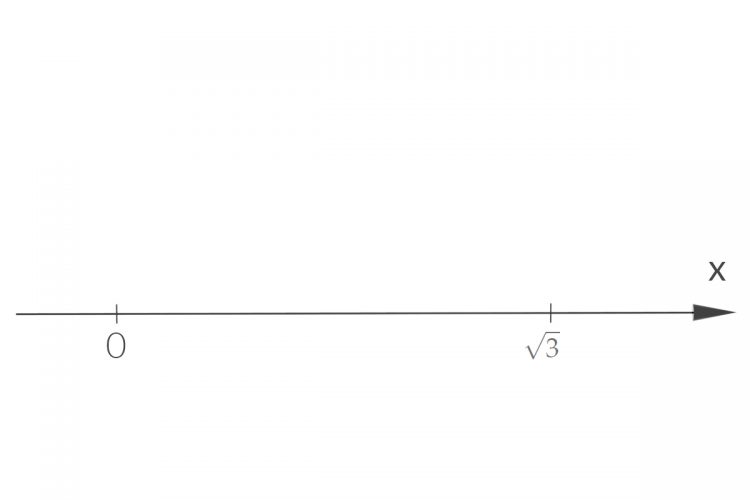
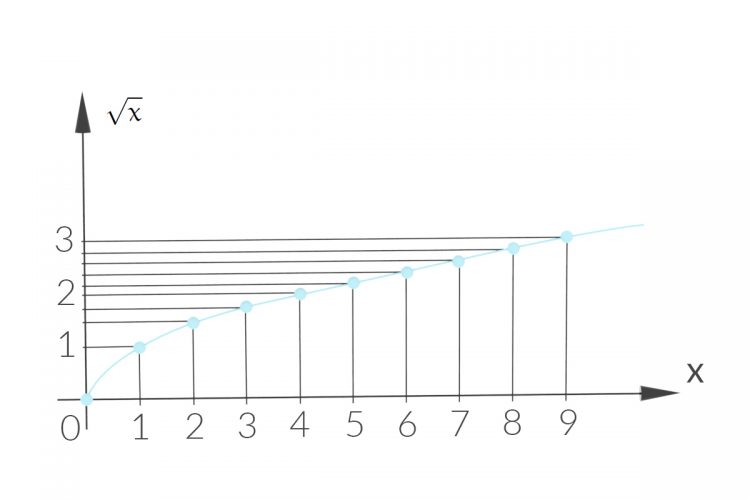
Max Ich habe den Zahlenstrahl schon oft in Matheschulbüchern oder Zeitungen gesehen, schon allein die Wurzelfunktion zeichnet man doch immer kontinuierlich:
Forcing
Rike Ja stimmt, das kam mit dem Erfolg der Diff-Int-Rechnung, und ich war damals fest davon überzeugt – aus eben solchen Gründen. Doch neulich habe ich über Paul Cohens Forcing-Methode gelesen.
Max Forcing-Methode?
Rike Ja, das ist die Methode, mit der er gezeigt hat, dass man die Kontinuumshypothese nicht entscheiden kann.
Max Okay.
Rike Er hat gerade das Argument, dass für die Mächtigkeit der Menge der Teilmengen in 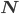
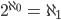
gilt, zum Anlass genommen, 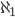
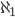
Max Cohen hat wohl ein ziemlich großes Abstraktionsvermögen?
Paul Cohen
Rike Ja, das hat er wohl. Er war visionär, er hat Gödel hinterfragt, er hat sich ausgemalt, was wäre, wenn 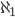
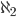
»Jedermann wird zustimmten – ob man daran glaubt, dass Mengentheorie einen Bezug zur existierenden Realität hat oder eben nicht – dass es eine Ästhetik in ihrer Einfachheit und in ihrer Tragweite gibt. Jemand, der Mengen als vollständiges Ganzes zurückweist, der in einer ätherischen Flüssigkeit schwimmt – jenseits aller direkten menschlichen Erfahrungen –, der hat die beeindruckende Aufgabe der Erklärung, woher diese Schönheit kommt. Doch wie kann jemand andererseits annehmen, dass so etwas wie das Kontinuum existiert, wenn es keine Möglichkeit gibt, dieses prinzipiell zu erforschen, oder noch schlimmer, die Menge aller Untermengen zu untersuchen, und zu sehen, ob es eine Menge von dazwischenliegender Mächtigkeit gibt? Mit den beiden Auswahlen konfrontiert, wähle ich die erste. Die einzige Realität, die wir wirklich begreifen, ist die unserer eigenen Erfahrung. Aber wir haben eine wunderbare Fähigkeit, etwas zu extrapolieren. Die Gesetze des Unendlichen sind Extrapolationen unserer eigenen Erfahrungen mit dem Endlichen. Wenn etwas unendlich ist, dann ist es vielleicht unsere wunderbare Intuition, die uns erlaubt zu fühlen, welche Axiome zu einem konsistenten und schönen System führen – wie unsere zeitgenössische Mengentheorie. Die ultimative Stellungnahme zur Kontinuumshypothese muss in menschlichen, nahezu sozialen Begriffen geschehen. Wir werden solange debattieren, experimentieren, beweisen und vermuten, bis eine Darstellung entsteht, die unseren wunderbaren Arbeitgeber befriedigt – und das ist unsere Intuition. Wie ich schon in meiner Monographie vor einigen Jahren schrieb, denke ich, dass der Konsens dahin geht, dass die Kontinuumshypothese falsch ist. Die Intuition, die mich am meisten zufrieden stellt, ist die folgende: Das Trennungsaxiom, das Ersetzungsaxiom und das Potenzmengenaxiom sind in gewisser Hinsicht orthogonal zueinander. Keine Methode des Beschreibens einer Kardinalzahl mittels einer Typ-Eigenschaft, die man auch im Ersetzungsaxiom benutzt, (hier muss ich etwas vage bleiben) kann adäquat die Größe des Kontinuums beschreiben. So fühle ich, dass 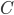
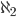
Max Hmmm, gefällt mir.
***
Übungsaufgabe
Zeige, dass die obige Relation für Folgen rationaler Zahlen eine Äquivalenzrelation ist.
Lösung
Diese Relation ist selbstverständlich reflexiv und symmetrisch, sie ist transitiv:
Sind

und
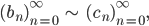
dann ist
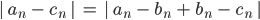
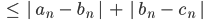
wegen der Dreiecksungleichung für den Betrag rationaler Zahlen, beide Summanden gehen nach Voraussetzung nach Null, also ist