Max und Rike sind im Schwimmbad. Rike sieht, wie das Wasser bei Max spritzt. Und als er dann anschlägt, freut sie sich und sagt ihm, dass sie sich jetzt die Kontinuumshypothese besser vorstellen kann. Die Tropfen des Wassers sind diskret und vereinigen sich zu dem “großen” Wasser, dem Kontinuum. Warum soll man das nicht verstehen?
Max Hey! Schwimmen ist anders als Handball! 50 m im Wasser sind anstrengender als in der Halle!
Wassertropfen und Volumen als Metapher
Rike Hey Max! Ich habe bei Deinem Anschlag grade die Kontinuumshypothese verstanden. Das Wasser ist eine wunderbare Metapher!
Max ich verstehe gar nichts! Lass uns eine Pause machen und Du erklärst mir das Wasser!
Rike Ja, gut. Als Du angeschlagen hast, hat das Wasser ganz doll gespritzt. Und danach sind die meisten Tropfen ins Becken zurückgefallen und haben sich mit dem Wasser im Becken vereinigt.
Max Ja, das sah bestimmt super aus!
Rike Ich hatte das Gefühl, dass ich mir viele Tropfen vorstellen und begreifen kann, aber ebenso auch das Kontinuum, das Wasser, was nicht mehr aus abzählbar unendlich vielen Tropfen besteht, sondern eine neuen “Dimension” hat.
Max Okay, was ist das Problem?
Rike Die Kontinuumshypothese stammt von Georg Cantor. Er hat versucht, Mengen, und genauer: Mengen von Zahlen genauer zu beschreiben. Er hat Äquivalenzklassen von Mengen dadurch gebildet, dass er die Elemente 1:1 abgebildet hat. Alle Mengen, die den natürlichen Zahlen gleichmächtig sind, also 1:1 abgebildet werden können, hat Cantor die Mächtigkeit Aleph 0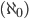 
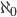
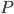
Max Verstehe
Teilmengen natürlicher Zahlen
Rike Und als man versucht hat, die Teilmengen der natürlichen Zahlen zu nummerieren, ist man gescheitert.
Max Glaub' ich nicht!
Rike Doch! Wenn wir hier 2 Gläser Cola haben, also Deins und meins:
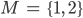
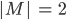
dann kannst Du daraus die Teilmengen
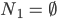
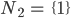
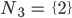
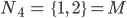
bilden. Das sind 4 , also
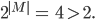
Cantor konnte zeigen, dass das auch für Mengen mit abzählbar unendlich vielen Elementen gilt.
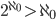
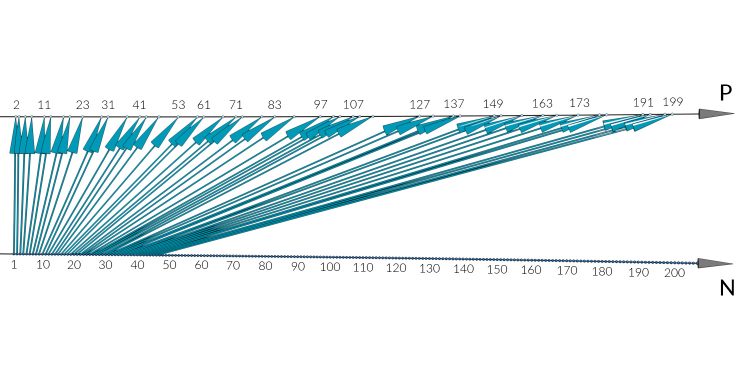
Er hat die nächste Kardinalzahl Aleph 1 (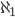
) genannt:
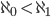
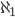
Max Okay!
Die Kontinuumshypothese
Rike Doch diese Eigenschaft,
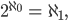
dem Kontinuum die nächste Kardinalzahl nach den natürlichen Zahlen zuzuordnen, ist nicht zu entscheiden oder zu beweisen. Sie heißt Kontinuumshypothese.
Max Wieso kann man das nicht entscheiden?
Rike Es hat sich herausgestellt, dass man
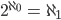
akzeptieren aber auch ablehnen kann. Diese Aussage ist nicht entscheidbar, sie ist unabhängig.
Max Doch Du stehst auf der Seite, dass
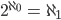
richtig ist, das hast Du doch gefühlt?
Rike Naja, immerhin kann ich das Volumen des Wassers und auch die Oberfläche berechnen, es gibt viele mathematische Methoden für das Kontinuum, die gut funktionieren.
Max Okay, vielleicht hat Cantor auch das Wasser beim Schwimmen beobachtet?
Rike Hey Max, Du hast recht, jetzt bin ich auf der klassischen Cantor-Borel-Lebesgues-Welle mitgeschwommen, sie ist so einfach, so anschaulich und so schön!
Max Haha!
***
Übungsaufgaben
- Finde weitere Beispiele von Mengen, die mit N gleichmächtig sind!
- Was bedeutet es, wenn die Kontinuumshypothese falsch ist?
Lösungen
- Gerade natürliche Zahlen, Quadratzahlen
- Dann ist