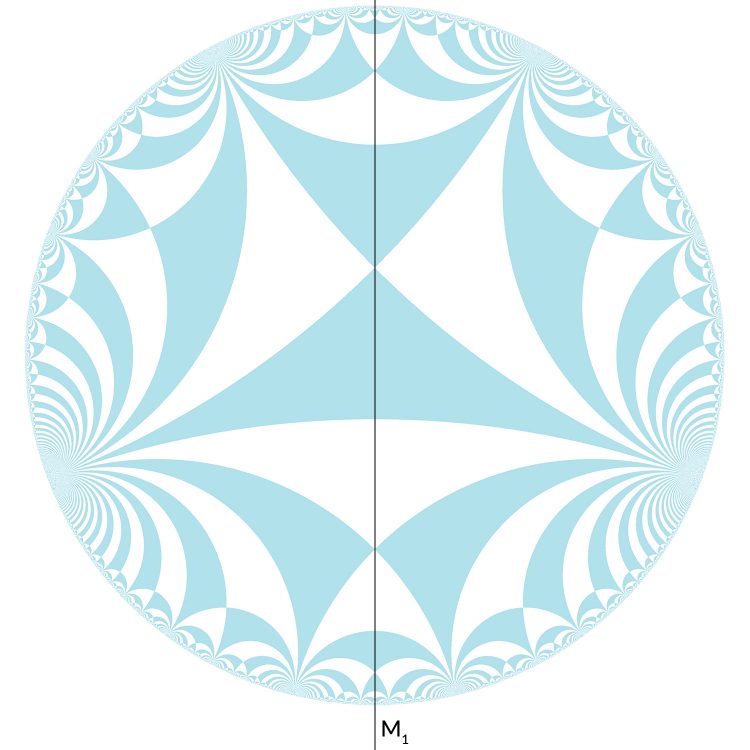
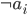Rike arbeitet weiter an ihrem Spiel im hyperbolischen Raum. Sie hat ein großes Bild mit einer hübschen Parkettierung in ihrem Loft aufgehängt. Max und Rike bestaunen es. Max gefällt es nicht.
Rike Hey Max, warum gefällt Dir das nicht? Eine tolle hyperbolische Parkettierung!
Max Ach Rike, hier haben wir doch nur eine Spiegelsymmetrie!
Ist das nicht etwas wenig? Keine Rotationssymmetrie? Das Muster besteht aus Dreiecken – wie das letzte. Aber hier treffen sich einige Dreiecke mit 3 anderen Dreiecken und an anderen Ecken kommen unendlich viele in einem Punkt zusammen.
Rike Du hast recht, etwas wenig Symmetrie. Aber genau das gefällt mir. Hier kann man etwas entdecken, es ist nicht so ausgewogen und durchgestylt. Ich habe neulich Lob der Mathematik von Alain Badiou gelesen. Badiou sagt, dass solche Sachen auch eine Logik bekommen, wenn auch nicht die klassische.
Nichtklassische Logik
Max Hatten wir nicht schon mal eine nichtklassische Logik?
Rike Ja, wir hatten eine mehrwertige Logik, da gab es ein "Etwas", "zur Hälfte" usw. Aber jetzt nehmen wir die Wahrheitswerte WAHR oder FALSCH (1 oder 0). Das sind die booleschen Werte.
Max Naja, etwas traditionell! Entweder – oder!
Rike Haha
Max Und wie weiter? Wenn Du die Parkettierung nicht magst aber ich mag sie, mögen wir sie dann zusammen?
Rike Nein.
Max Dann ist es ja doch klassisch traditionell!
Rike Schau mal, zunächst haben wir hier unsere Aussagen, ich mache das mal etwas einfacher, wir lassen mal nur endlich viel Aussagen 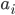
Max Ja, gut.
Boolesche Werte
Rike Wir ordnen jeder Aussage
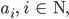
einen booleschen Wert zu und schreiben dafür 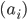
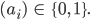
Max Machst Du mal ein Beispiel?
Rike Okay,
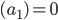
bedeutet, die erste Aussage führt zum Schluss, dass das Bild nicht gefällt.
Max Verstehe.
Das logische Und 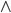
Rike Das logische Und 
| 0 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
Das logische Oder 
Das logische Oder 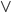
| 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Die Verneinung 

und schließlich gibt es noch die bekannte Negation 
| |
| 0 | 1 |
| 1 | 0 |
Max Okay, alles wie gehabt, nichts Neues!
Rike Doch, jetzt kommt die entscheidende Eigenschaft: Du kannst eine Art Abhängigkeit einer Aussage 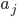
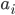
Aus 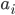
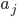
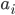
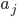
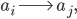
oder 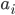
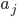




Max Hmmm
Rike Da wird in der klassischen Mathematik für Beweise oder in Herleitungen angewendet, es ist die logische Grundlage.
Max In Gottes Namen!
Rike In Booles Namen!
Max Und nun?
Rike Jetzt erkläre ich die sogenannte parakonsistente Logik mit den Symbolen 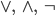
Aus 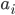
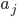
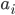
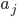

wird anders bestimmt:




Max Komisch! Alle Meinungen, die zum Gefallen eines Bildes führen, sind abhängig voneinander! Und jede Meinung, die zum Gegenteil führt, ist unabhängig!
Rike Stimmt!
Max Hey, dann bin ich ein unabhängiger (parakonsistenter) Symmetrie-Spezialist!
Rike Hahaha
***
Übungsaufgabe
Wo kann man außerdem parakonsistente Logik anwenden?