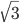Max und Rike sind wieder zu Hause. Rike programmiert weiter an ihrem Spiel im hyperbolischen Raum. Rike möchte, dass die Charaktere sich im hyperbolischen Raum heimisch fühlen. Sie kennen nur diese Geometrie. So ist der Boden mit Mustern parkettiert. Rike will solche Muster programmieren und erklärt Max die Prinzipien.
Max Hi Rike, wie bist Du vorangekommen?
Rike Hi Max, ganz gut. Ich habe mir jetzt ein Muster in der hyperbolischen Geometrie ausgewählt. Das hier von Tamfang!
Max Okay, nicht schlecht.
Rike Ja. Jetzt will ich sowas automatisch erzeugen.
Max Wie geht das?
Rike Zuerst musst Du es verstehen. Schau mal, hier:

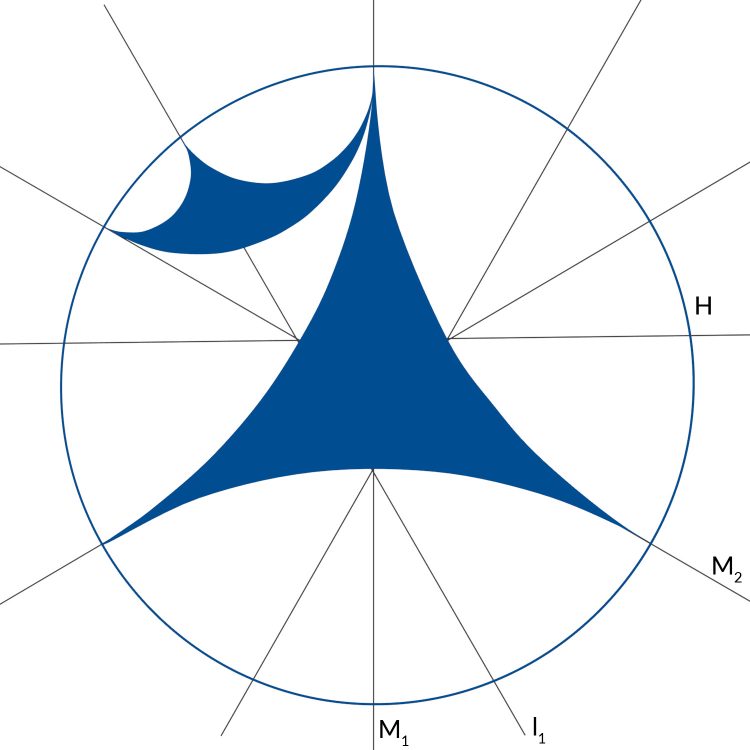
Erkennst Du da Symmetrien drin?
Symmetrien
Max Klar, ich kann es an der Mittellinie spiegeln.
Rike Richtig, aber Du kannst es auch an zwei weiteren “Mittellinien” spiegeln.
Max Okay, irgendwie habe ich wohl nicht die mathematische Brille auf.
Rike Na, und, siehst Du denn nicht, dass Du das Muster mit einer Drehung um 120° wieder in Deckung bringst?
Max Hmm
Rike 120° - Das ist eine Dritteldrehung, so haben wir zwei Symmetrie-Eigenschaften: 3 Spiegelachsen und 1/3-Drehung. So kann man solche Muster klassifizieren.
Geometrie

Max Gibt's denn noch was?
Rike Ja klar, bei diesem Muster hier haben wir nur Dreiecke und in jedem Eckpunkt treffen genauso viele zusammen.
Max Unendlich viele?
Rike Ja!
Max Deshalb musst Du die computergenerieren?
Rike Ja!
Max Und wie geht das?
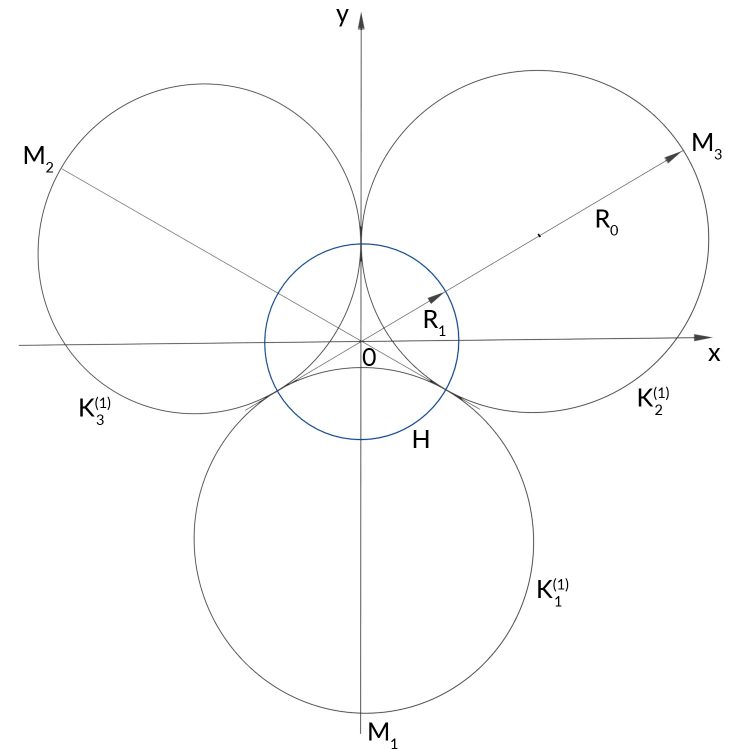
Rike Dieses Muster hier greift die hyperbolische Geometrie auf. Das hatte uns ja Antonija erklärt. Geraden in diesem Poincaré Disk Modell sind direkte Verbindungen, sie sind eigentlich Kreise, die den äußeren Kreis H im rechten Winkel treffen.
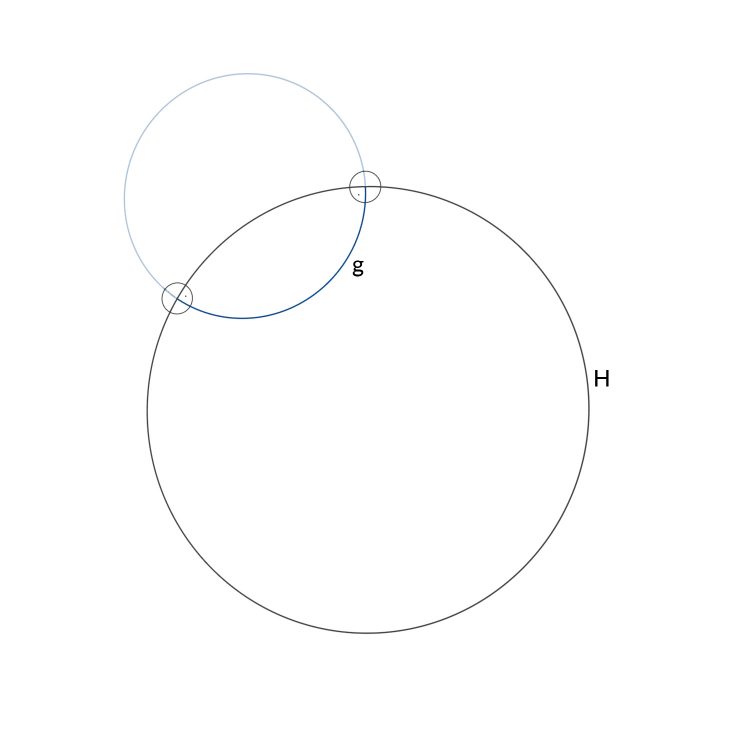
Und dieses Muster greift das gut auf.
Konstruktion – Level 0
Zuerst konstruieren ich diese drei Kreise Ki(1), i = 1, 2, 3, die das Dreieck bilden.
Max Okay!
Rike Jetzt färbst das erste Dreieck, das Mutterdreieck, das Dreieck vom Level 0 ein.
Max Klar!
Konstruktion – Level 1
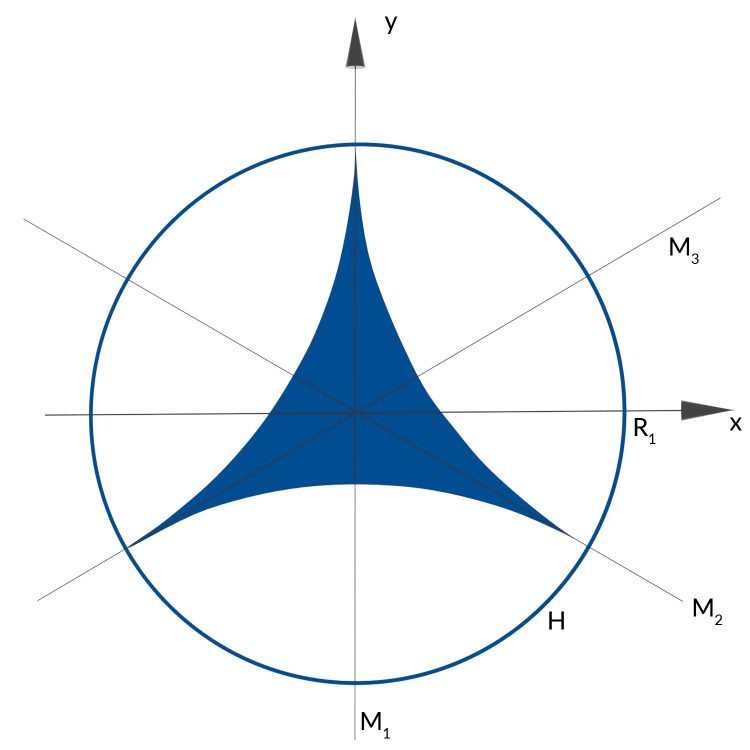
Rike Jetzt zeichnest Du die (euklidischen) Linien l1, l2 und l3.
Max Gut.
Rike Da, wo die Linie l1 den Kreis H trifft, wird der Eckpunkt des nächsten Dreiecks sein. Du musst nur noch die 3 Kreise Ki(2), i = 1, 2, 3, zeichnen, die immer senkrecht auf H treffen.
Max Okay.
Rike Jetzt kannst Du das entstandene Dreieck einfärben und gemäß unserer Symmetrie spiegeln und drehen.

Konstruktion – Level 2
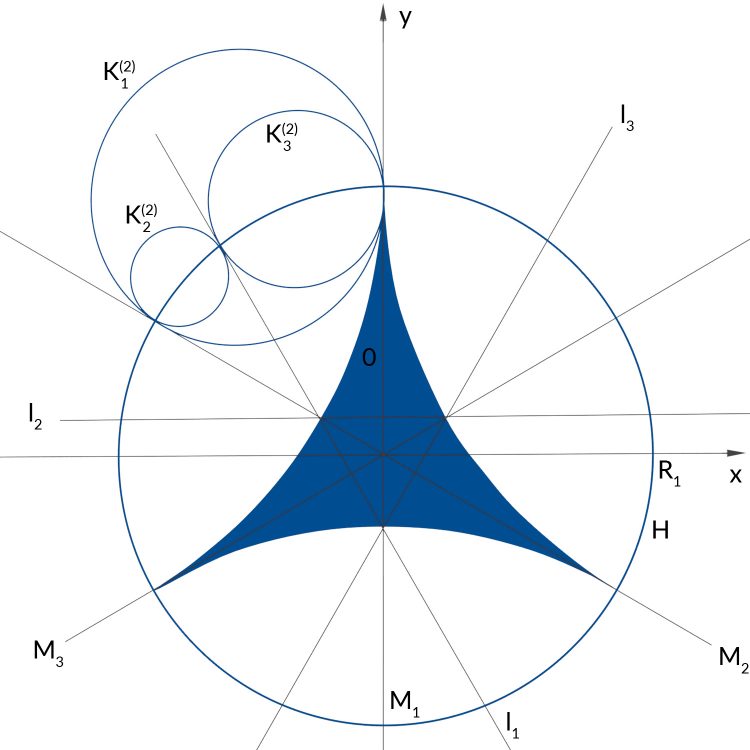
Max Okay. Und jetzt muß ich wieder Kreise zeichen? Aber wo liegt der Mittelpunkt?
Rike Hey, Max! Du hast doch die mathematische Brille auf. Jetzt kannst Du zwei Punkte P und Q frei auf H wählen und dann die Kreise wie bisher zeichnen. Es sind jetzt 4 Kreise Ki(3), i = 1, 2, 3, 4. Ich habe mal ein festes Seitenverhältnis für die Radien der kleinen und großen Kreise gewählt, nämlich 2 : 1, anders als Tamfang, aber prinzipiell kannst Du P und Q frei auf H wählen.
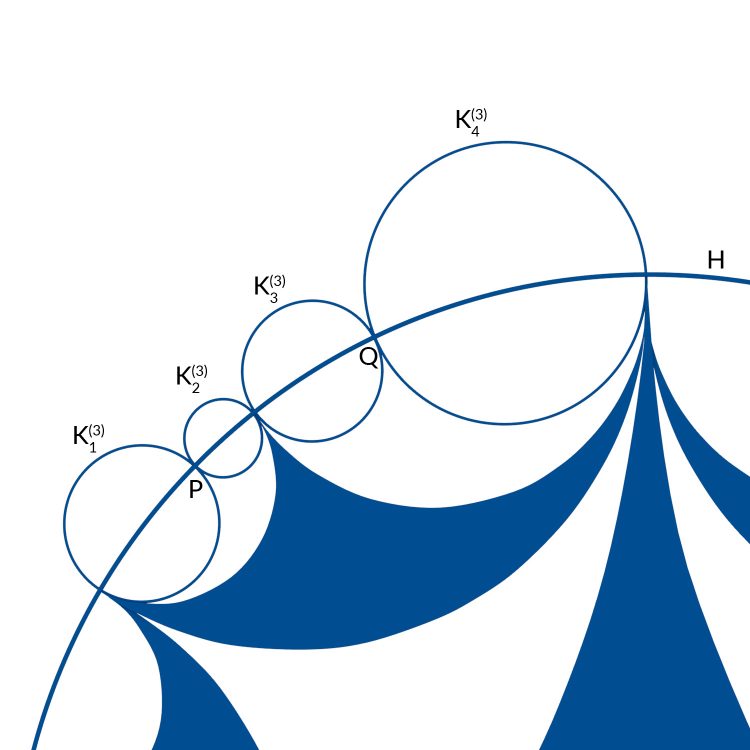
Fazit
Max Und das geht immer so weiter? Dann gibt es ja zweimal unendlich viele Möglichkeiten für diese Symmetrie und Geometrie!
***
Übungsaufgaben
Berechne das Verhältnis der Radien R0 und R1!
Lösung
R0 : R1 =