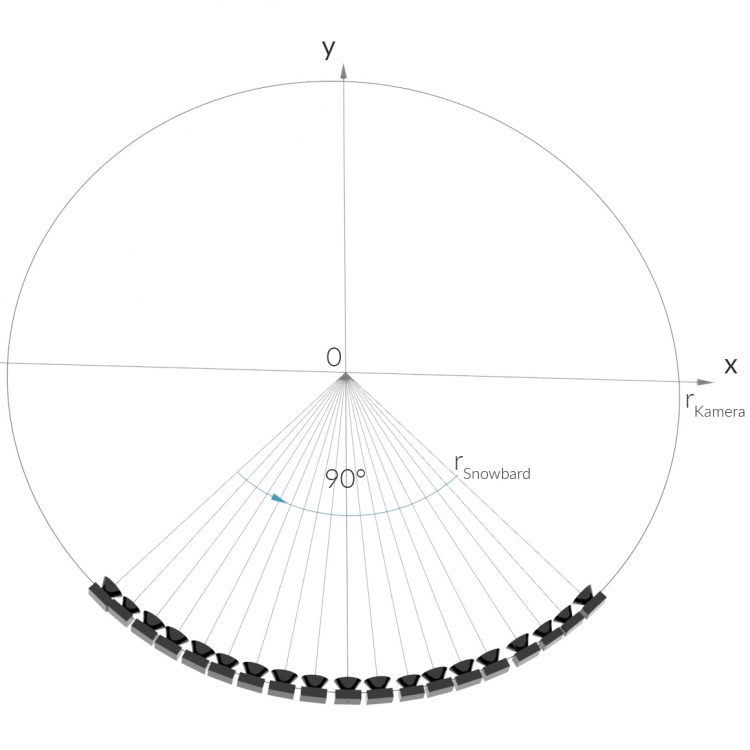
Max und Rike haben überraschend eine Anfrage erhalten, ein paar sportliche Fotos vom Snowboarden zu machen. Max möchte gern den Bullet Time-Effekt benutzen und fragt Rike, wie das geht.
Max Wir sollen ein paar Snowboard-Fotos machen, wollen wir mal den Bullet Time-Effekt ausprobieren? Was meinst Du?
Rike Coole Idee! Wir müssen ausrechnen, wie viele Kameras wir brauchen.
Max Okay.
Rike Wie lang ist denn der Weg für so ein Special?
Max Naja, lass uns mal so einen einfachen Flip nehmen, den können die Jungs bestimmt, ich zeigs Dir mal.
Rike Okay, Du bist jetzt hier eine Kurve gefahren, da muss ich mal den Radius messen, und außerdem muss ich noch die Zeit messen. Kannst Du das noch mal vorführen?
Max Okay!
Berechnung des Weges
Rike Okay, Du warst ca. 1 s in der Luft, und der Radius von Deinem Viertelkreis ist etwa
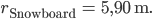
Da haben wir einen zurückgelegten Weg von einem Viertelkreisumfang:
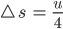
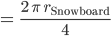
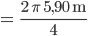
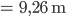
Max Okay, für 1 s brauche ich bei so schnellen Bewegungen 30 Frames pro Sekunde (fps), also im normalen Video hätten wir 30 Frames für den Flip. Wenn ich 30 Fotokameras auf dem Viertelkreis aufstelle, kriege ich 30 Fotos hintereinander, und kann damit ein normales Video erzeugen. Aber das reicht nicht!
Rike Was willst Du denn für eine Zeitlupe haben?
Max Naja, schon deutlich mehr als zweifach. Bei Matrix haben sie das gemacht und hatten eine 10-fache Zeitlupe, 1999! Jetzt haben wir 2018 und jeder hat eine Kamera.
Anzahl der Kameras
Rike Gut, Du suchst so viele Kameras zusammen, wie möglich, ich rechne Dir die Belichtungszeit aus: Sagen wir mal, wir haben 150 Kameras. Dann kann jede Kamera den 150ten Teil des Weges und der Zeit fotografieren, dann wird nichts doppelt fotografiert, das sind
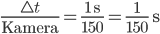
Unsere Vollbildkameras haben 1/160 s als mögliche Belichtungszeit oder Du nimmst 1/200 s.
Max Dann haben wir nicht den vollen Zeitraum überdeckt!
Rike Stimmt! Aber auf unserer Seite ist die Trägheit des Auges, es merkt ja auch nicht die diskrete Abfolge der Einzelbilder zu einem “Bewegtbild”.
Max Okay, je kürzer die Belichtungszeit, umso schärfer wird die Bewegung, umso mehr Kameras brauche ich! Dann sprechen wir einfach alle an, das klappt schon!
Rike Okay, und wie lösen wir die Kameras eine nach der anderen aus? Kennst Du jemanden, der sich mit solchen Synchronisationen auskennt?
Max Ja, ich glaub' schon!
Übungsaufgabe
Berechne die Geschwindigkeit, die ein Fahrzeug für eine "normale" Videokamera auf dem Viertelkreis mit dem Radius von 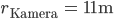
Lösung
62 km/h