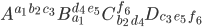Max, Rike und Matthew treffen sich im Schnee. Rike fragt ihn, was ihn am meisten in der Mathematik fasziniert. Matthew erzählt von seinem Traumarbeitsgebiet.
Matthew You know, ich liebe mathematische Physik, wie auch Quantenmechanik und allgemeine Relativitätstheorie. Beide Theorien sind etabliert, gelten aber für verschiedene Zweige der Physik. Das Zusammenwirken steht noch aus – sowohl physikalisch als auch mathematisch. Alle Experimente, die den Einfluss der Gravitation auf Quantensysteme messen, werden physikalisch mit der nichtrelativistischen newtonschen Gravitation beschrieben. Und auf der anderen Seite nimmt man für die Relativitätstheorie die klassischen physikalischen Methoden. Jetzt gibt es ein Experiment, wo einzelne Photononen der Gravitation unterworfen werden. Man hat einzelne Photonen mit verschiedenen Phasen erzeugt und sie an einer schweren Masse vorbeigeführt. Danach hat man die einzelnen Photonen nicht unterscheiden können und nur eine Überlagerung festgestellt. Sowohl ihre Position als auch ihre Ausgangszustände waren nicht feststellbar.
Max Ja, so fühle ich mich auch manchmal, ich weiß nicht, wer ich bin, wo ich bin, und wie ich hierhergekommen bin.
Rike Hahaha. Es ist aber noch viel weitreichender. Wenn die Teilchen keine Geschichte haben, so auch die Elektronen und Moleküle, aus denen wir aufgebaut sind, wie können wir dann eine Geschichte haben? An so etwas Schwieriges wagst Du Dich heran, Matthew?
Matthew In Cambridge habe ich ein paar Vorträge von ein paar Physikern dazu gehört. Sie waren so jung und so erfrischend, you know. Ich hätte Lust, da als Mathematiker mitzumachen. Sie versuchen, die Wechselwirkungen von Teilchen mit neuen Modellen für Tensoren zu beschreiben, und das gefällt mir.
Tensoren
Max Tensoren?
Matthew Yes, Tensoren. You know, Du nimmst für jedes Teilchen einen Hilbertraum – so eine Art Vektorraum mit einem Skalarprodukt, mit dem man dann auch Abstände definieren kann, also 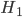
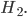
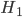
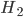
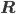
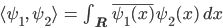
Dann kannst Du leicht das Tensorprodukt von 2 Funktionen definieren:
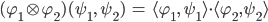
Max Hmmm.
Matthew Du kannst sogar ein Skalarprodukt in diesem Tensorraum definieren und diese Tensoren wieder zu einem Hilbertraum machen, dem Tensorprodukt 
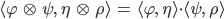
usw. So kannst Du mit

sehr gut innerhalb der Quantenmechanik zwei Zustände eines Teilchens beschreiben, 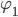
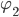
Max Okay
Matthew Schwieriger wird es, wenn es um “dieselben” Teilchen geht, die verschiedene Zustände annehmen. Wenn
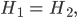
dann ist
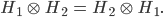
Dieser Tensorraum 
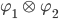
steht für das Elektron mit dem "+"-Spin. Jetzt lass uns alles tauschen in diesem Tensor:


Dann wird aus dem einen Zustand – mit dem positiven Spin – sein Gegenteil, der Zustand mit "-"-Spin, then we get:
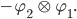
Jedes Elektron kann natürlich nur einen Zustand annehmen. Aber im mathematischen Modell, im Tensorraum zweier Hilberträumen benutzen wir die Überlagerung der beiden, das gibt:
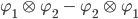
Das sind sozusagen die elementaren Elemente in 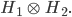
Max Kann man nicht einfach die beiden
gleich setzen:
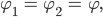
dann ist
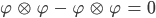
Matthew Nein, das ist nicht sinnvoll, diese 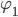
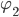
Max Hmmm.
Matthew Mit diesem Zustand
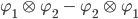
haben wir praktisch die Koexistenz der beiden Zustände formuliert, und so etwas wurde ja jetzt für Photonen untersucht. Aber diese Notation beschreibt nicht, w i e die beiden Zustände ineinander übergehen. Jetzt habe ich bei Lucien Hardy eine neue Schreibweise für Tensoren gefunden, die bipartite notation:
Neue Tensoren
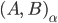
steht dann für die Vereinigung oder Wechselwirkung von 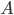
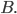
geschieht, ist 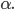
Das Ordnungsunabhängigkeitsaxiom
Für ein System aus mehreren Teilen
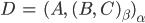
lassen sich 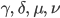
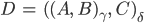
und
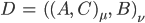
Und, noch besser, you know, 
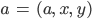


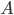

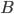
Das können wir mit in die Bezeichnung hineinnehmen:
![]()
Max Okay
Matthew Und so kannst Du schreiben
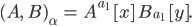
Max Okay
Matthew Die Ortsinformation stecken wir mal in die Systeme 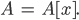
Max Okay
Matthew Damit kannst Du jetzt schon Systeme mit 3 Komponenten und nicht trivialer Wechselwirkung notieren, zum Beispiel:
Das ergibt
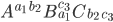
Max Klar!
Matthew Oder solche:
Ich finds cool.
Max Ich auch.
Rike Ich auch.
***
Übungsaufgabe
Schreibe das Tensorschema für das System aus 4 Komponenten.
Lösung