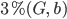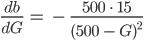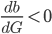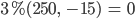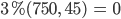Max, Rike und Matthew treffen sich beim schönsten Aussichtspunkt. Matthew (20) kommt aus England, studiert Mathe in Cambridge. Gestern Abend hatten sich die Drei bei einer Party kennengelernt. Rike hatte schon von dem Mathebuch Mathematik heute und dem grandiosen Einstieg in die Prozentrechnung erzählt. Aber nun holt sie endlich das Buch aus ihrem Rucksack.
Rike Hi, Max, hi, Matthew, schön, dass wir uns treffen.
Max Hi Rike!
Matthew Hi, Rike!
Rike Hier schau mal, wie die deutsche Prozentrechnung in der 7. Klasse vermittelt wird. Hier sind die Begriffe:
Definition p %
Prozentsatz p %: Bruch mit dem Nenner 100 und dem Zähler p:
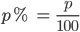
Man verwendet den Prozentsatz als 'Operator'.
Grundwert G: Größe, auf die der Prozentsatz angewendet wird.
Prozentwert P: Die Größe, die man nach Anwendung des Prozentsatzes erhält.
Matthew Wow, cool. You know, das mit dem Operator gefällt mir, ist doch klar:
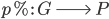
G und P sind nicht näher angegeben? Dann nehmen wir mal 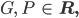

Max Okay, ich würde auch die reellen Zahlen nehmen.
Matthew Gibts denn keine Vorschriften, was der Operator macht?
Beispiel aus Mathematik heute
Rike Es gibt ein Beispiel:
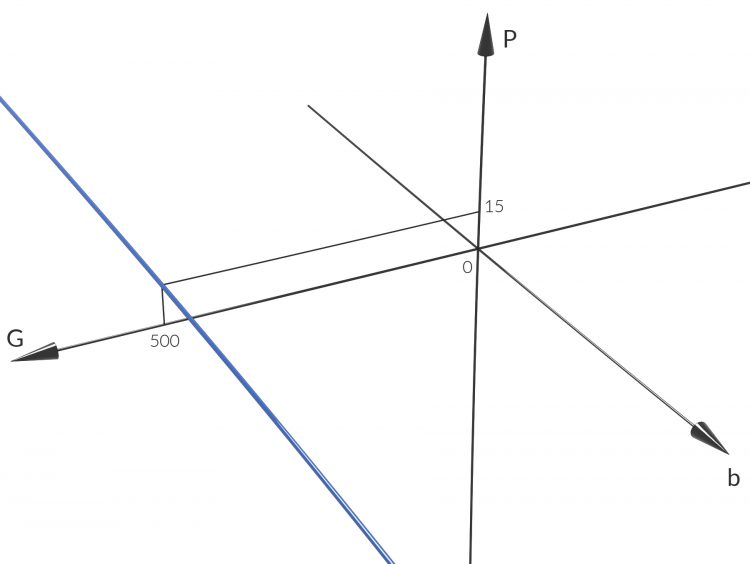
Mit dem Grundwert G = 500 und dem Prozentsatz 3 % erhält man den Prozentwert von P = 15:
Matthew Ja schön, dann haben wir so eine Art Fixpunkt für die Abbildung. Ich schlage vor, wir machen den einfachsten Ansatz für den Operator:
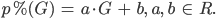
Und für das Beispiel haben wir
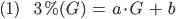
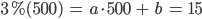
Naja, das ist eine einfache Gleichung, da haben wir eine Relation zwischen a und b.
Max Stimmt.
Matthew Die würde ich mal nach a umstellen:
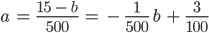
Max Richtig
Matthew Und wenn wir das in die Gleichung (1) einsetzen, kriegen wir
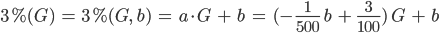
Formel (2)
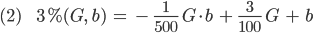
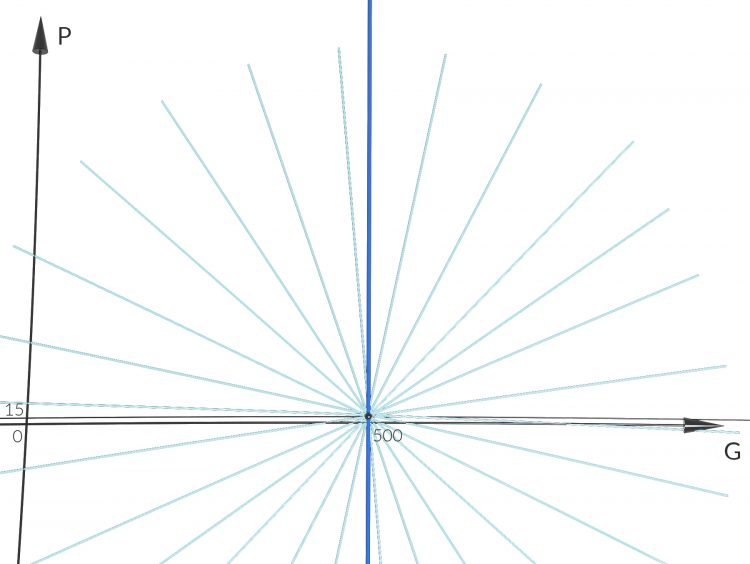
Für G, b nahe Null ergibt das
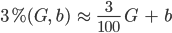
Das ist eine Ebene, die durch Null geht und in G-Richtung sehr gering ansteigt, mit einem Anstieg von 3/100, das sind ca. 0,0005°.
Und für G, b sehr groß, 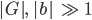
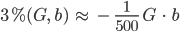
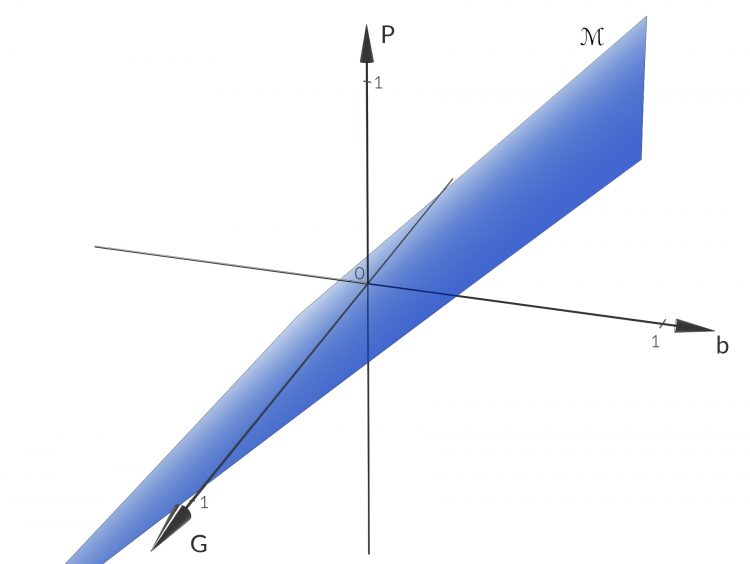
Riemannsche Mannigfaltigkeit
Insgesamt haben wir eine richtig nice diffentiable manifold, shall we say 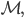
Max Cool!
Matthew Unsere super Formel (2) hat eine Besonderheit, nämlich bei G = 500 ist
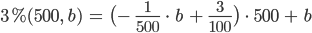
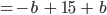
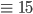
Also
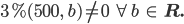
Nullstellen
You know, jetzt lasst uns mal die Nullstellen von
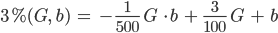
ausrechnen:
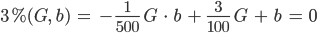
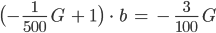
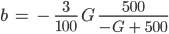
You know, die Nullstellen liegen bei
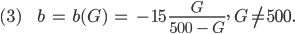
Max Okay, bei G = 500 wird das Ergebnis sowieso nicht Null, 3 % von 500 sind 15.
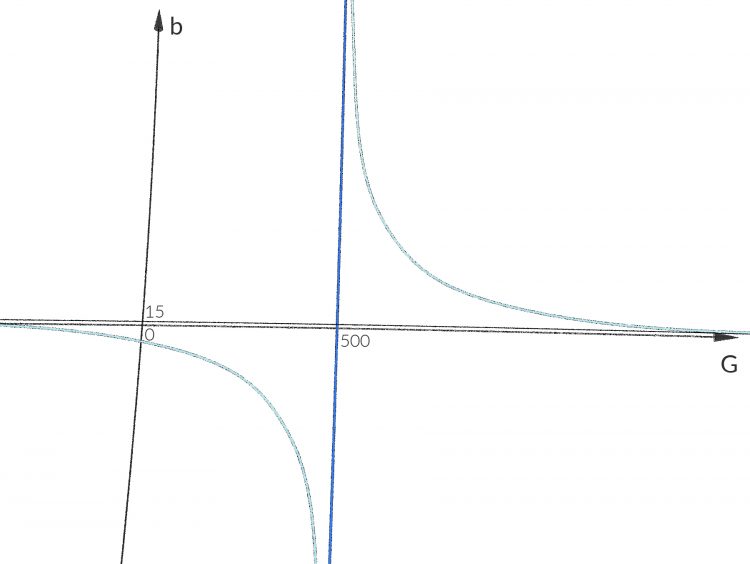
Matthew Right, diese Formel gibt ein schönes Bild. I love it.
Das sind die Kurven, in denen sich the Riemannian mit der Nullebene schneidet. Das sind die Punke (G, b) mit
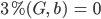
Die Kurven haben sehr schöne Eigenschaften, you know, die sind immer fallend, da können ja die Kids mal die Ableitung ausrechen, okay? Und was habe ich nun hergeleitet:
Paradoxa
Very, very nice geometry, very nice curves für die Nullstellen (3)! Mit unserem Ansatz (1) kriegen wir die Formel (2) für den 3 %-Operator, und daraus ein paar paradoxe Ergebnisse, you know:
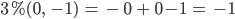
oder
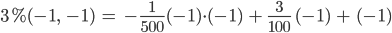
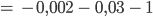
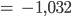
oder
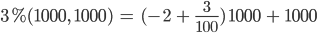
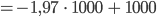
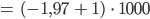
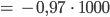
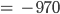
Max Was, Du berechnest 3 % von 1000 mit -970? Und 3 % von -1 ist -1?
Matthew Yes – mit Eurem deutschen Operatorzugang!
Rike Hahahahahaha!
***
Übungsaufgaben
- Berechne für die Gleichung der Nullstellen (3) die Ableitung
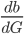
- Was kannst Du über das Vorzeichen herausfinden?
- Finde weitere paradoxe Werte für