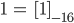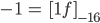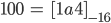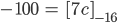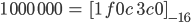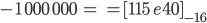Positionssysteme mit negativer Basis

Rike und Max sind nun wieder zu Hause. Sie treffen sich in Rikes Loft. Rike hat sich für die Bewohner ihrer virtuellen (hyperbolischen) Welt besondere Zahlensysteme ausgedacht. Da sieht man einer Zahl nicht mehr so einfach ihren Wert an. Außerdem hat jede Stadt in Hyperland ihre eigene Währung. So braucht zum Umrechnen einen kleinen Rechner oder ein Smartphone. Max soll das jetzt mal austesten.

Max Hi, Rike, wenn ich das austesten soll, muss ich das erstmal verstehen.

Binärsystem

Rike Okay. Erinnerst Du Dich an das Binärsystem?

Max Okay, kenne ich.

Rike Da haben wir die Basis 2

und jede Zahl kannst Du als Summe

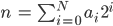
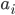
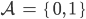
schreiben. Die sind dann die Ziffern aus dem Alphabet

und man kann dann mit der Basis 2 darstellen, indem man nur die Ziffern schreibt, mit der größten beginnend:

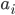
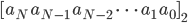
Max Okay, Rike, das hatte ich vor laaaanger Zeit, mach doch mal ein einfaches Beispiel!

Rike Lass uns 256 nehmen, das ist eine Zweierpotenz,…

Max …, stimmt,

Rike Richtig, das schreibst Du also als Summe:

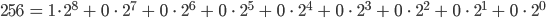
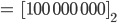
Max Okay, ich erinnere mich.

Algorithmus

Rike Ich habe noch ein anderes Verfahren gefunden, um diese auszurechen. Das geht so: Du teilst 256 durch die Basis 2 und ermittelst den Rest:

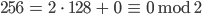
Max Okay.

Rike Dieser Rest 0 ist die letzte Ziffer der Binärdarstellung, also

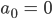
Max Okay.

Rike Jetzt nimmst Du den Rest und ziehst ihn von der Ausgangszahl ab, teilst das durch die Basis 2 und erhälst

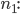
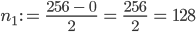
Für 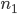berechnest Du wieder den Rest bei der Division durch 2:

Max Das ist 0.

Rike Stimmt, das wird dann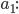

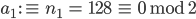
Max Gut.

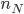
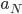
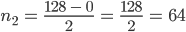
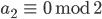
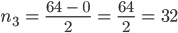
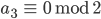
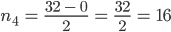
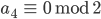
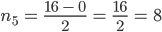
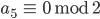
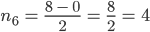
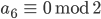
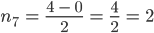
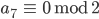
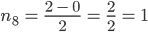
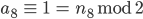
Rike Das machst Du so weiter, bis der Quotient gleich dem Rest ist:

Max Na, gut. Ist vielleicht ein Verfahren, was Du gut programmieren kannst, aber die Binärdarstellung ist nicht neu.

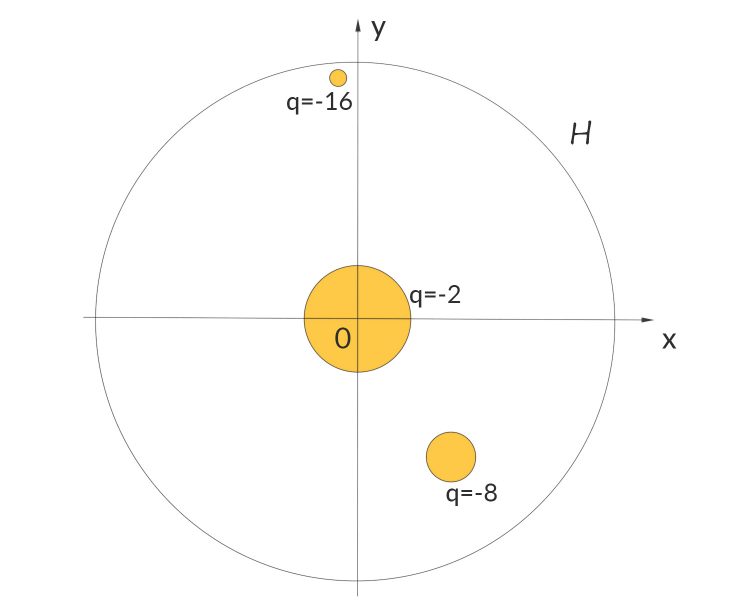
Rike Das stimmt, das gibt‘s schon sehr lange. In meinem Spiel aber soll das so eine Art Parallelwelt sein. Die Leute in den verschiedenen Städten sind sehr eigenwillig und jede Stadt hat ihre eigene Währung. Das muss natürlich was ganz anderes sein als wir das kennen. In der Mitte von Hyperland ist es am einfachsten; die Leute sind ärmer dran. Am Hyperlandrand haben die Leute viel mehr Geld und rechnen in anderen Größenordnungen.

Max Hmm.

Negative Basis

Rike Die erste Idee ist, das jetzt die Basis 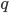negativ ist.

Du kannst nämlich jede Zahl auch als Summe der folgenden Art schreiben:

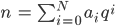
und

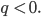
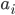
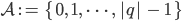
Dann sind die Ziffern aus dem Alphabet:

Max Kann ich mir schwer vorstellen.

Beispiel mit q=-2

Rike Der Stadt in der Hyperlandmitte habe ich die Basis

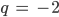
gegeben. Lass uns dasselbe Beispiel noch mal mit 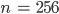zur Basis -2 rechnen.

Max Gut.

Rike Das geht so:

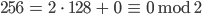
also

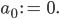
Dann

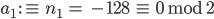
usw.

…

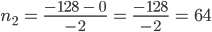
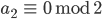
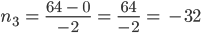
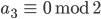
Max Okay, ist nicht

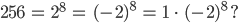
Rike Ja, richtig.

Max Also kriegst Du

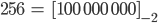
Rike Stimmt.

Max Wozu brauchst Du denn dieses negative Binärsystem?

Negative Zahlen

Rike Damit kann ich auch negative ganze Zahlen "negativ binär" ohne Minuszeichen ausdrücken.

Max Was? Wie geht das? Mach doch mal ein Beispiel! Nimm doch mal

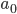
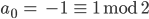
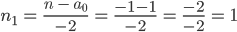
Rike Okay! ermitteln wir wieder als Rest bei der Division von durch 2:

Fertig!

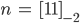
Max Hey! Da sieht man nicht so leicht, ob man Schulden hat!

Rike Doch, das lernen die Hyperlandkinder in der 1. Klasse!

***

Übungsaufgaben

1. Schreibe den Formalismus zur Berechnung der für auf!
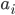
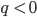
2. Berechne für die Darstellung zur Basis und
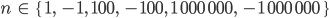
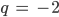
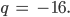
3. Wie erkennt man, ob eine Zahl negativ ist?

Lösungen

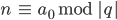
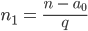
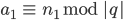
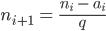
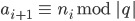
1. bis

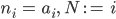
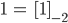
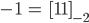
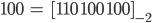
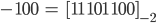
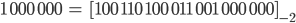
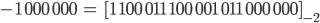
2. Für haben wir das Alphabet

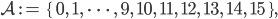
   was wir wie üblicherweise mit

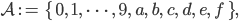
   identifizieren.

3. ist ungerade.