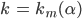Mathematik rauer Oberflächen

In virtuellen Welten trifft man viel viel mehr Mathematik, als man sich vorstellen kann. Hier kommen Funktionen vor, die in keinem Mathestudium besprochen werden, keiner Mathelehrerin und keinem Mathelehrer auf normalem Weg begegnen oder die es gar ins Abi schaffen.

Bei der Erstellung virtueller Welten oder bei der fotorealistischen Nachbildung realer Welten mit 3D-Programmen wird die physikalische Korrektheit immer wichtiger. So hat man in den Anfangsjahren einer glänzenden Kugel einfach an geeigneter Stelle einen weißen Punkt verpasst, wo heute aufwendige Rechnungen gemacht werden.

In den letzten Jahren hat sich in Richtung physikalischer Korrektheit einiges getan, wir verwiesen bereits auf das Buch mit Renderalgorithmen und dem C++ Source Code von Pharr et al. Im April trugen Andrea Weidlich (Weta) und Dylan Sisson (Pixar) in Stuttgart auf der FMX-Tagung vor. Beide betonten die physikalische Korrektheit der Abbildungen. Insbesondere beschäftigen sich Pixar und Weta mit neuen Modellen von Oberflächen und stellen die inzwischen standardisierten Begriffe wie Diffuse Map oder Glossiness in Frage und untersuchen stattdessen die Rauigkeit von Oberflächen. Haptisch ist das ganz klar, wer kennt nicht “Streichelbücher” für die Kleinsten. Aber wie kann man so etwas mathematisch fassen?

Das Phong-Modell

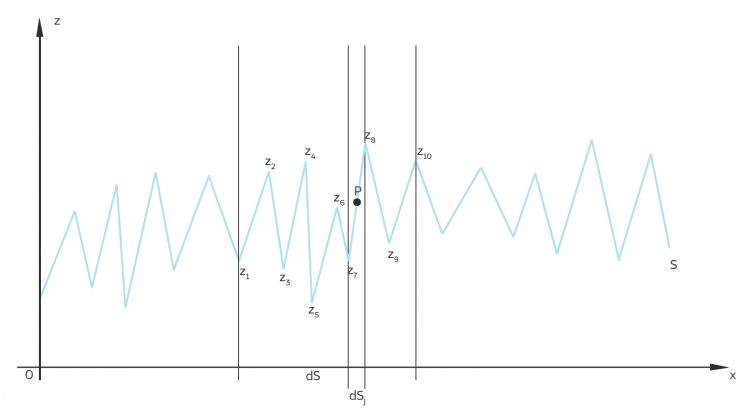
Ein einfaches Modell ist folgendes: Man möchte gern die Lichtstreuung k an einem Punkt P einer (geeigneten) Oberfläche S berechnen. Dazu muss man die Richtung des einfallenden Lichtes kennen und gestattet dem Besucher, mit einer frei platzierbaren Kamera C in (View-)Richtung V auf den Punkt P zu schauen. k wird als Faktor verstanden: kV soll das gestreute Licht sein.

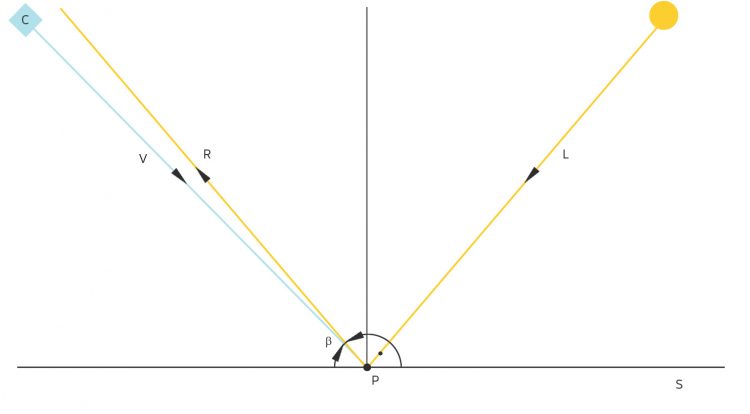
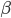
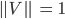
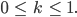
Der Vektor V wird skaliert und damit ist kV dann das in Richtung C gestreute Licht. Aus Gründen der Energieerhaltung ist

Sollte k aufgrund von formalen Rechnungen negativ sein, wird

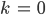
gesetzt.

Das Phong-Modell berechnet nun den Winkel 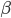zwischen dem an S reflektierten Licht R und der Richtung V. k wird als Skalarprodukt von R und V definiert, R und V werden auf die Länge 1 skaliert:

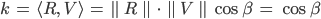
Als Maß für die Rauigkeit eines Materials wird eine benutzerdefinierte Variable n eingeführt:

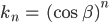
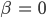
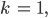
Fallen R und V zusammen, so ist und folglich das bedeutet totale Reflexion. Dieses Phong-Modell eignet sich für besonders glänzende, hell reflektierende Oberflächen und wird meist für industriell hergestellte Oberflächen wie Plastik verwendet.

Das Microfacet-Modell

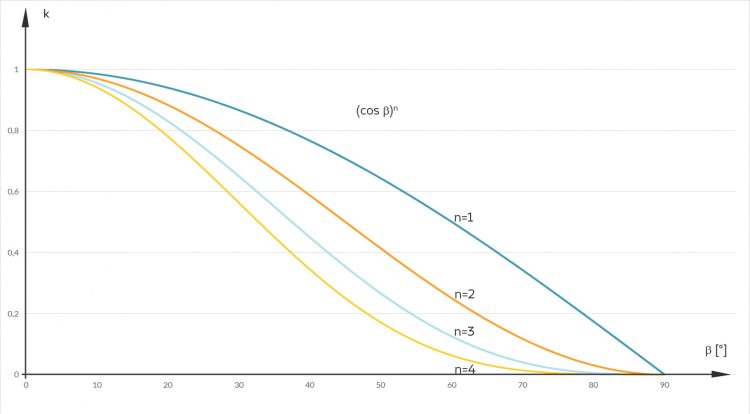
Das obige Phong-Modell ist natürlich sehr einfach. Damit gelingt es zwar, glänzende Oberflächen zu beschreiben, aber raue kann man damit nicht realistisch beschreiben. Doch es gibt noch eine Reihe anderer Modelle. Eins davon, das wir dem Phong gegenüberstellen, heißt Microfacet. Es beruht darauf, die Oberfläche S in kleine Flächen dS zu zerlegen; und jedes dieser Flächenstückchen dS mit linearen Flächen 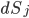 stückweise zusammenzusetzen.

Eine raue Oberfläche wird in der folgenden Formel für die Lichtstreuung durch eine Zahl m charakterisiert: Das ist das quadratische Mittel m der M Höhenpunkte :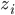

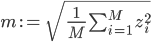
Betrachten wir nun so einen linearen Teil eines Flächenstückchens . Auch hier haben wir die Lichtrichtung L, die Kamera C aus der Richtung V. Wir können leicht den Normalenvektor N dieses Flächenteils berechnen. Die Winkelhalbierende H von V und L lässt sich ebenfalls leicht berechnen. sei der Winkel zwischen der Normalen N und der Winkelhalbierenden H:

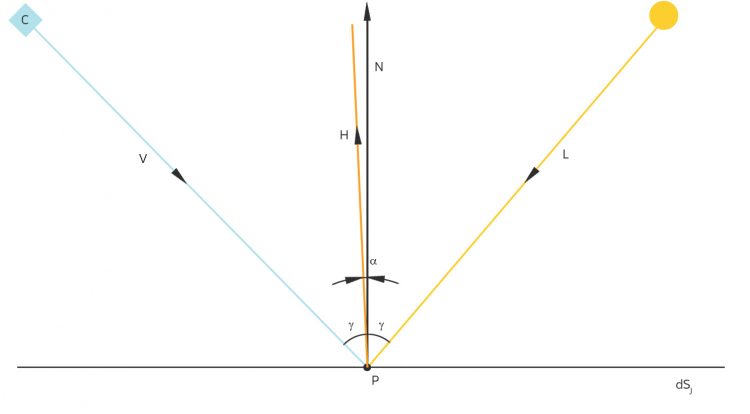
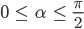
Sollte der Winkel größer als oder negativ sein, so wird der Streufaktor k Null gesetzt:

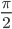
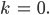
Die Beckmann-Verteilung

Beckmann und Spizzichino stellten für elektromagnetische Wellen ein Streumodell vor:

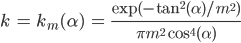
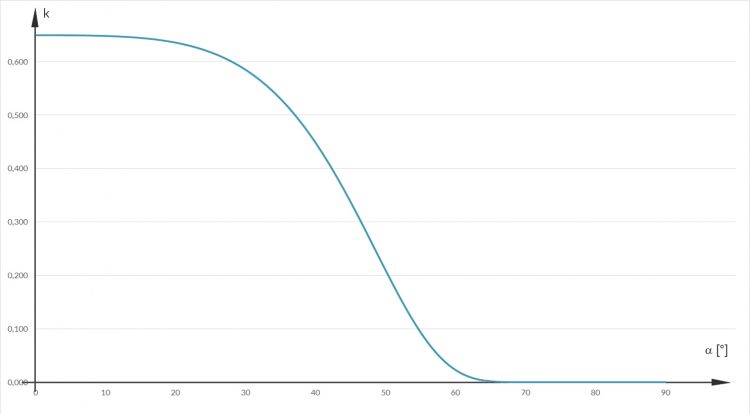
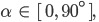
Es ist natürlich auch möglich,  Inhomogenitäten für jede räumliche Richtung einzubauen, siehe Pharr, S. 538.

Vergleicht man nun dieselbe Oberfläche, so ist offensichtlich die Microfacet-Oberfläche dunkler, erstens ist k < 1; zweitens wird im Mittel nur jede 2. Fläche 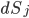reflektieren, weil sie entweder bzgl. L oder C verdeckt ist. Aufgrund der Zerlegung der Oberfläche in viele Teile und deren Lichtstreuungsberechnung, bekommt das von uns modellierte Objekt eine viel detailreichere und rauere Oberfläche.

***

Übungsaufgabe

Diskutiere die Kurvenschar in Abhängigkeit von m.