Rike hat ihr Game nun beendet und muss ihr Loft räumen. Sie hat sich rechtzeitig um einen neuen Job gekümmert und hat Anschluss an die Startup-Szene in Bielefeld gefunden. Heute nun zieht sie von Zuhause aus. Max hilft ihr natürlich. Sie haben einen kleinen Lieferwagen gemietet. Doch auf der Landstraße nach Bielefeld gab es eine unübersichtliche Stelle mit einer blöden Linkskurve, plötzlich war dann Gegenverkehr und sie mussten ausweichen.
Rike Oh Gott, zum Glück hat uns der Bauer geholfen.
Max Ja, zum Glück wohnt mein Opa hier bei Bielefeld.
Rike Naja das Wichtigste ist, dass dem Computer nichts passiert ist.
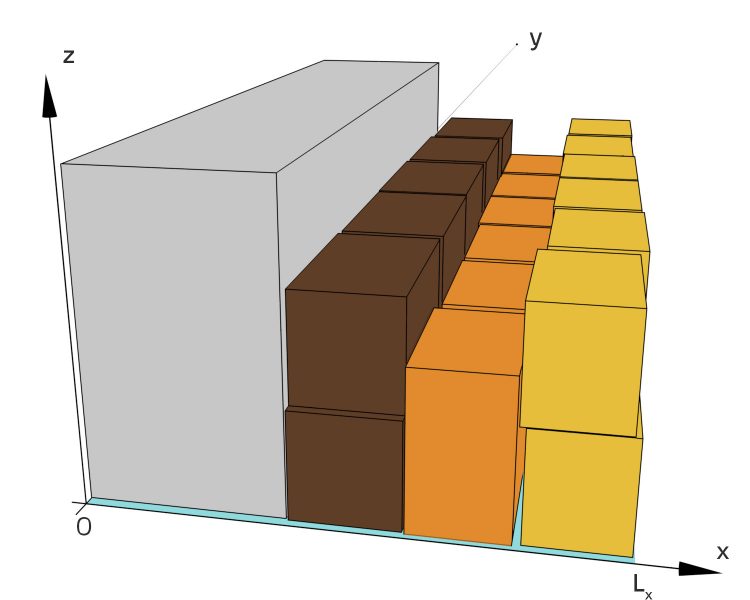
Rikes Ladestrategie
Max Hast du den Schwerpunkt der Ladung nicht richtig berechnet?
Rike Ich habe das Fahrrad nach links gestellt, weil es angegurtet werden kann, daneben die normalen Umzugskartons, dann meine Hardware und ganz rechts die Bücherkisten. Die PCs und Bildschirme sollten gut geschützt sein. Das war mir wichtig.
Max Wollen wir den Schwerpunkt jetzt zusammen berechnen?
Rike Okay, das muss wohl sein. Also, ich habe ein verpacktes Fahrrad:
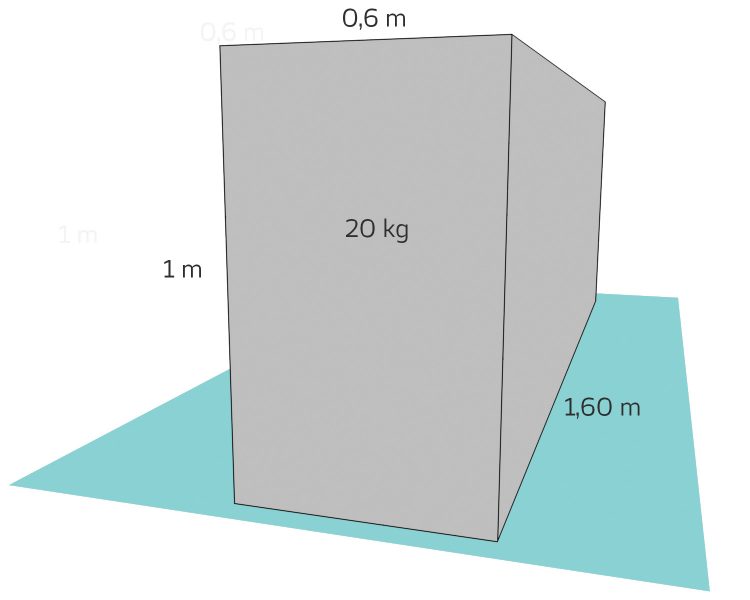
Max Okay, gut verpackt.
Rike Daneben habe ich normale Umzugskartons, 10 Stück:
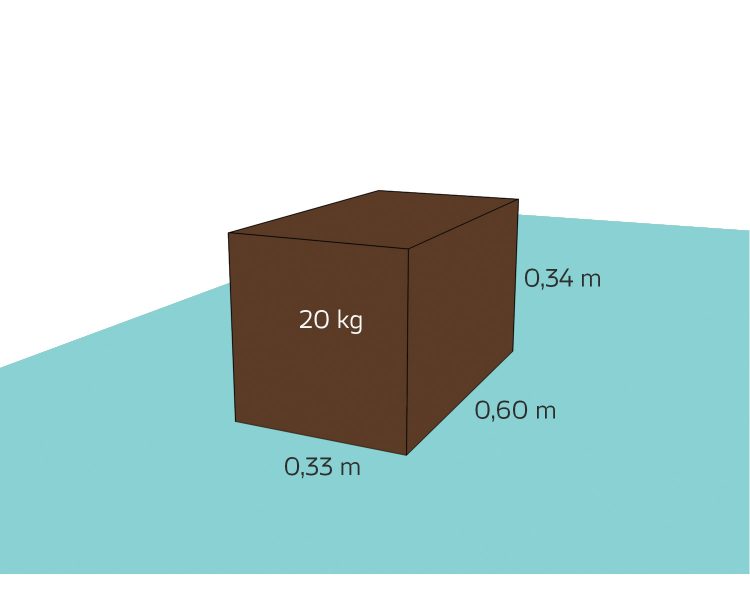
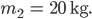
dann meine Hardware in 6 Standardkisten:
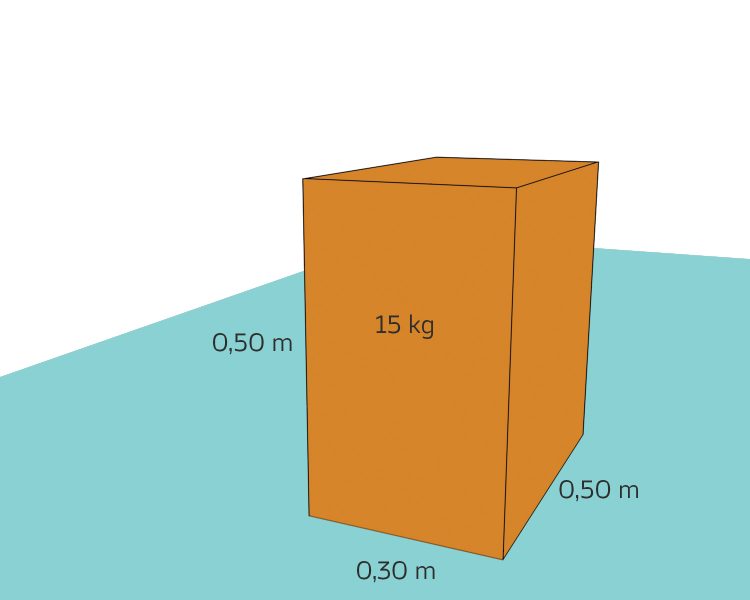
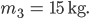
Und zum Schluss die Bücherkisten, das sind, wart‘ mal, 12 Stück:
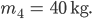
Berechnung der gesamten Ladungsmasse
Max Wollen wir erst mal die Gesamtmasse bestimmen?
Rike Ja klar. Die Masse M der Ladung ist die Summe der geladenen Massen 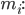
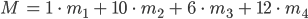
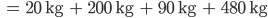
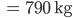
Max Ganz ordentlich!
Rike Weißt Du, die Massen sind in die Wagentiefe nahezu gleichmäßig verteilt. In jeder Kiste habe ich meine Sachen auch recht gleichmäßig verteilt.
Max Okay, typisch mathematisch.
Rike Okay. Den Schwerpunkt 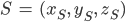
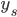
Max Der liegt bestimmt nicht in der Mitte!
Schwerpunkt als Massenmittelwert
Rike Richtig! Da habe ich mir gedacht, wir nehmen den Begriff des Mittelwertes.
Max Ja gut, das ist der Massenmittelpunkt.
Rike Jetzt brauchen wir die Massenverteilung entlang der x-Achse, so eine Art Dichte 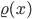
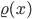
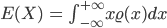
Weil unsere Dichte 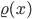
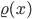
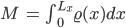
Also ist
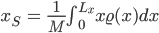
Max Okay. Aber wie kriegen wir die Dichte?
Rike Das ist nicht schwer.
Eindimensionale Ladungsdichte
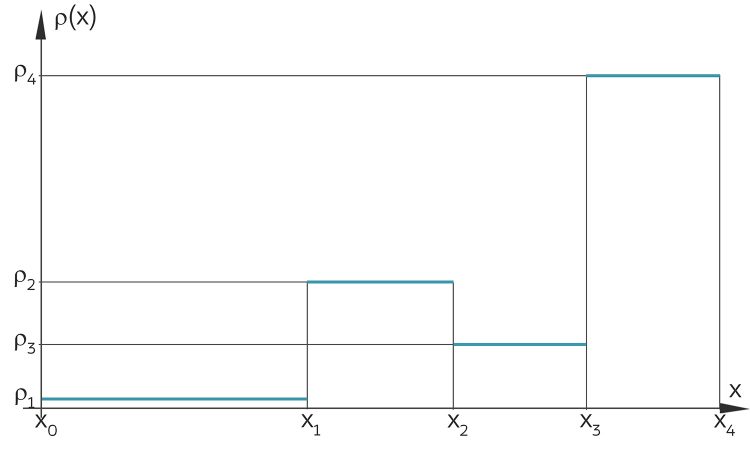
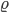 in x-Richtung.
in x-Richtung.
Die Dichten 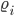
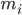
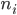
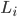
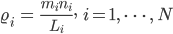
Max Verstehe. Dann ist das Integral doch lösbar, wenn 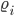
Herleitung der Formel für xS
Rike Max, stimmt! Wir kriegen:
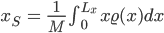
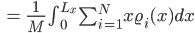
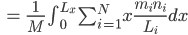
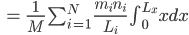
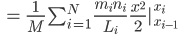
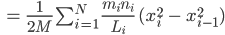
Jetzt nehmen wir den dritten binomischen Satz
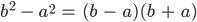
und kommen weiter:
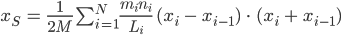
Wegen
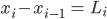
ist nun
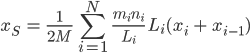
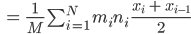
Finale Formel für xS
Also final:
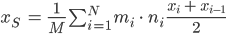
Max Hmmm.
Rike Schau mal, diese letzten Summanden
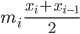
sind gerade die Mittelwerte jeder Box - multipliziert mit ihrer Masse.
Max Ja gut, und in Zahlen, kriegen wir…. Soll ich mal?
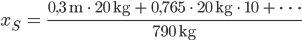
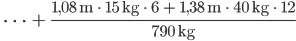
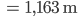
Hey! Die Ladebreite war 1,53 m! Das ist ja weit aus der Mitte! In jeder Linkskurve wird Dein PC nach außen gedrückt. Wir müssen die Ladung umsortieren!
Rike Schade, wenn wir immer nur Rechtskurven nach Bielefeld hätten, hätte ich optimal gepackt, aber ich muss wohl von Links- u n d Rechtskurven ausgehen.
Max Ich helfe Dir.
Rike Danke!
***
Übungsaufgaben
- Prüfe, ob das Integral über die Massendichte die Gesamtmasse ergibt.
- Gibt es eine optimale Lösung der Ladungsverteilung?
- Berechne
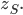
Lösungen
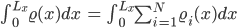
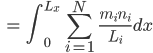
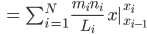
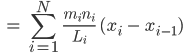
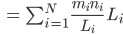
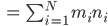
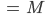
- Ja
- 0,34 m