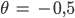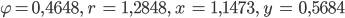Rike hat ihre erste Woche in Bielefeld in ihrem neuen Job überstanden. Mit Max nimmt sie eine kleine Auszeit. Sie gehen hier im schönsten Wald spazieren und entdecken mathematische Formen in der Natur. Im Frühjahr haben Farne auffällige Spiralformen. Doch auch im Sommer wachsen die Farne und bilden Spiralen aus, wenn sie ihre Blätter auffalten. Karl Bloßfeldt hat das genial fotografiert und diese (u.a.) Formen der Natur Urformen der Kunst genannt. Daran erinnert sie sich und diskutiert gleich die Formel für die Farne.
Urformen der Kunst
Max Hey, Rike, diese Farne, die haben ja echt tolle Formen, sogar im Sommer!
Rike Ja stimmt, sieht wirklich toll aus. Die Natur ist wirklich unergründlich. Karl Bloßfeldt hat das fotografiert, er nennt solche Formen Urformen der Kunst.
Max Was meint er damit?
Rike Er meint, dass solche geometrischen Formen in der Natur das Original sind - und als Vorbild für die Kunst herhalten können.
Max Hey, dann haben wir heute Natur- und Kunsterlebnisse!
Rike Stimmt.
Max Kann man die denn mit Formeln beschreiben, also um sie zu reproduzieren, wo sie doch so wichtig sind?
Bildungsgesetz der goldenen Spirale
Rike Warte mal, in der Natur kommen meist sogenannte goldene Spiralen vor, das sind solche: Der Radius r verkleinert oder vergrößert sich in Abhängigkeit vom Winkel 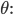
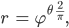
alles in Polarkoordinaten, 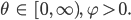
Umrechnung von Polarkoordinaten in kartesische Koordinaten
Max Kann man das auch als Funktion in x-und y-Koordinaten schreiben?
Rike Ja klar, das geht so:
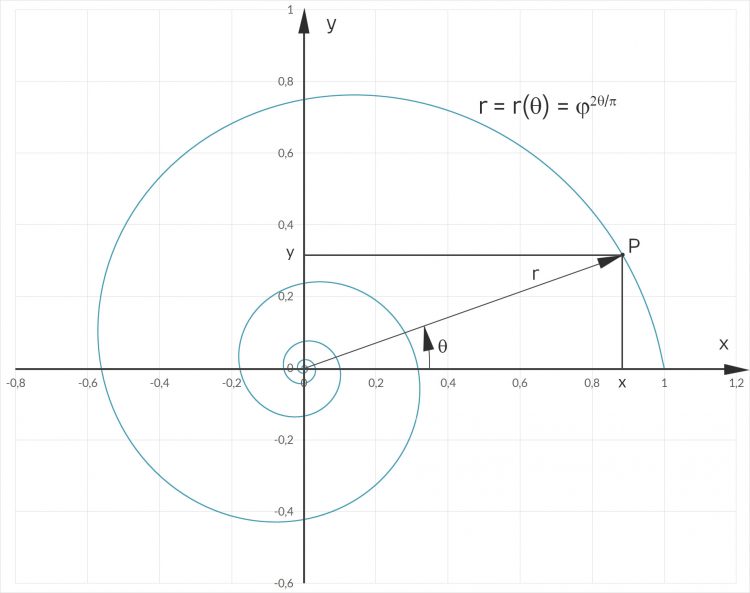
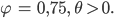
Wenn Du zu einem Punkt P mit Radius r und Winkel 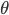
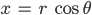
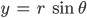
ist. Und umgekehrt:
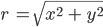
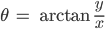
... und ein paar Fallunterscheidungen für die einzelnen Quadranten.
Max Klar. Rike, Deine Spirale sieht irgendwie so harmonisch aus!
Rike Richtig, sie hat einige Eigenschaften vom goldenen Schnitt. Sowas lieben Künstler. Und Mathematiker finden, dass der Radius r sehr schnell nach Null geht für 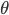
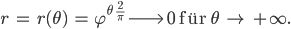
und
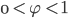
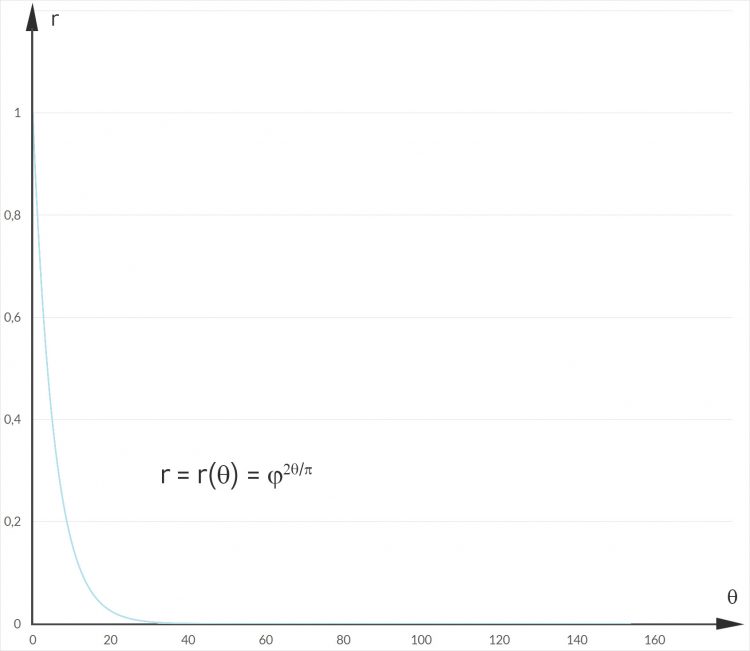
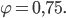
Max Aber sag mal Rike, so ganz trifft die Formel die Form der Farne nicht. Der Radius geht viel zu schnell nach Null. Die Krümmung ist immer gleich, in Deinem Bild hat die Spirale immer eine Linkskrümmung. Wollen wir das nicht mal anders herum probieren, wir nehmen 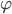
Rike Hey Max!
Max Das mit der Krümmung, das sieht man doch sofort!
Neue goldene Spirale
Rike Okay, lass uns
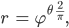
mit 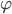
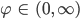
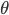
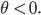
Max Okay.
Rike Dann haben wir ein besseres asymptotisches Verhalten:
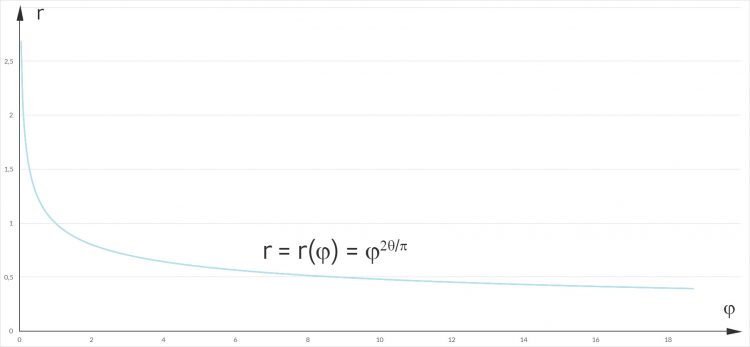

Max Ja, das gefällt mir. Und wie sieht die Spirale aus?
Rike Hier, schau:
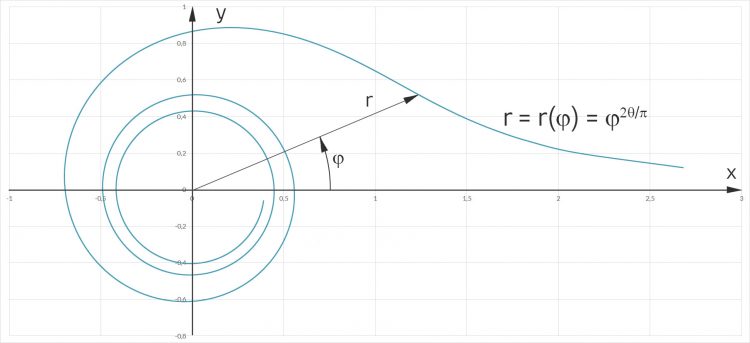
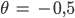
Max Hey, das gefällt mir. Hier ändert sich sogar die Krümmung, wie bei Farnen! Kannst Du das ausrechnen?
Rike Hahaha!
***
Übungsaufgabe
Überprüfe, ob die Krümmung der neuen goldenen Spirale Null werden kann!
Lösung
Wir betrachten die Spirale als Kurve
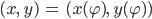
Die 2. Ableitung ist gegeben durch
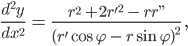
dabei ist für
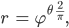
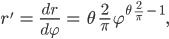
und entsprechend
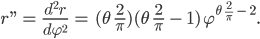
Die 2. Ableitung wird Null, genau dann, wenn
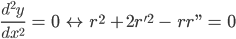
Durch Einsetzen der Ableitungen und einfache Umformungen erhält man die Stelle der Krümmungsänderung mit
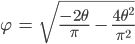
In unserem Beispiel mit