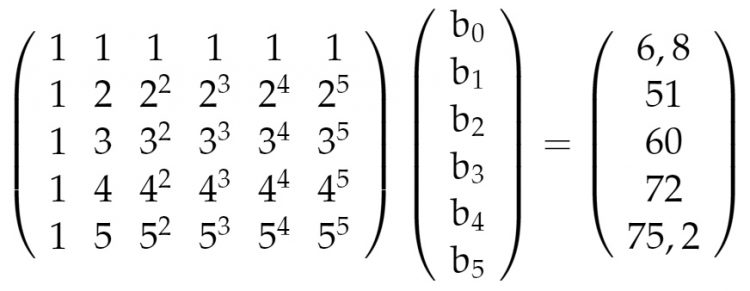Rike fängt langsam an, sich in ihrem Büro einzuleben. Ihr Unternehmen will ein Spiel entwickeln mit Locations, die in 3D erstellt werden. Rike soll 3D-Szenen konstruieren, aber auch Marketing und Admin machen. Weil die Finanzierung noch nicht klar ist oder nicht ausreicht, bietet das Unternehmen auch andere Dienstleistungen an: Audiovisuelle Produkte, 3D-Produktvisualisierung, “Erklär-Videos” für technische Prozesse usw.
Heute Abend kommt Max zu Besuch. Sie wollen zusammen was in Bielefeld unternehmen. Doch Rike sitzt noch an ihrer Arbeit. Sie erklärt sie Max:
Rike Wir haben den Auftrag, für ein Umweltunternehmen ein paar Diagramme zu erstellen und mathematisch zu beleuchten.
Das Problem
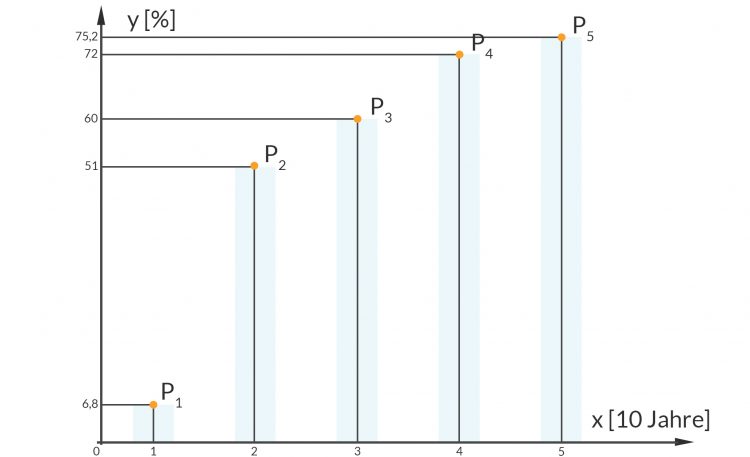
Es sind in Nature mehrere Artikel zur Antarktis erschienen. Sie zeigen verschiedene besorgniserregende Szenarien der geologischen, biologischen und sozialen Entwicklungen auf. Das veränderte menschliche Verhalten scheint schuld daran zu sein, dass es ganz schlimm kommt. Ein Autor beruft sich u.a. auf eine japanische Studie, in der gefunden wurde, dass sich die Menschen immer weniger in der Natur aufhalten. Insbesondere haben nur 6,8 % der japanischen 10-jährigen Kinder sich jemals in der Natur aufgehalten, sind auf Bäume geklettert oder haben ein Tier beobachtet, während 60-75 % der Kinder früherer Generationen das gemacht haben. Ich soll Zwischenwerte gerade bei den 10- bis 20-Jährigen berechnen und darüber hinaus. Schau mal hier, das ist das Diagramm:
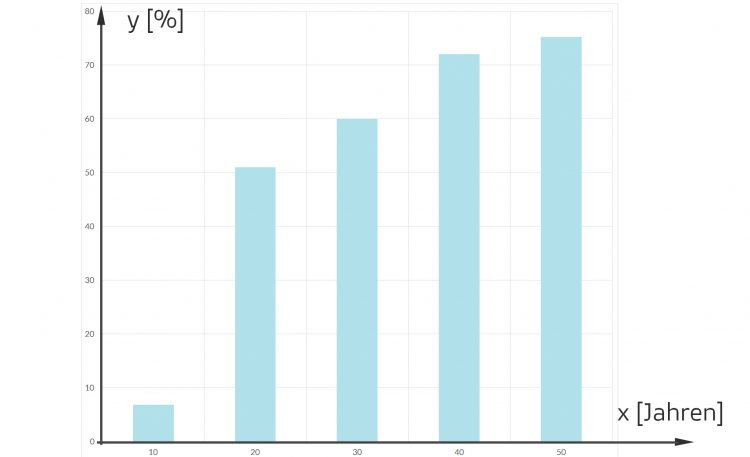
Max Hey Rike, ist das wahr, dass die Kinder kaum noch draußen spielen? Auch kein Handball oder Fußball? Mann!
Rike Max, die Studie meint die unberührte Natur und die Tierwelt. Hast Du schon mal eine Nacht in einem Zelt verbracht?
Max Klar! Im Trainingslager! Dann haben wir draußen Handball gespielt! Echt komisch!
Rike Haha, soll ich’s Dir weiter erklären?
Max Okay, sei doch nicht beleidigt!
Die "Informations"-Punkte 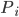
Rike Hmm. Dann habe ich die tatsächliche Information in 5 Punkten zusammengefasst, die x-Werte habe ich einfach mal 1, 2, …, 5 genannt, die stehen für 10-, 20-, … 50-Jährige, die y-Werte geben den Anteil der Menschen an, die in ihrer Kindheit die Natur direkt kennengelernt haben.
Max Okay!
Rike Jetzt habe ich ein Polynom gesucht, das durch die Punkte 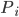
Max Warum hast Du denn ein Polynom gesucht? Wir hatten doch schon mal Splines?
Rike Stimmt. Wir hatten schon mal Splines. Das ist auch eine Näherung. Sie legt Polynome 3. Grades Stück für Stück durch die Punkte. Wir könnten hier auch eine solche Näherung konstruieren. Aber mir scheint sie etwas „künstlich“, eben sehr konstruiert zu sein. Jetzt suche ich eine Formel für alle 5 Punkte, das ist doch ein ganzheitlicher Ansatz!
Max Okay.
Rike Also, welchen Grad soll ich denn nehmen – Deiner Meinung nach?
Max Naja, für 2 Punkte kann ich eine Gerade finden, für 3 Punkte eine Parabel, das hatten wir mal in der Schule, und für 5 Punkte eben …. 4. Grades!
Der Polynomansatz
Rike Gut, nehmen wir
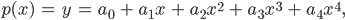
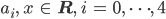
Dann setzen wir die Punkte ein und kriegen 5 Gleichungen, die schreiben wir gleich mal in Matrixschreibweise:
Das ist ein lineares Gleichungssystem, das kannst Du mit dem Gauß-Algorithmus lösen, ich habe das dank Arndt-Brunner numerisch gelöst:
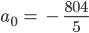
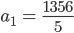
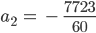
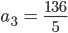
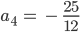
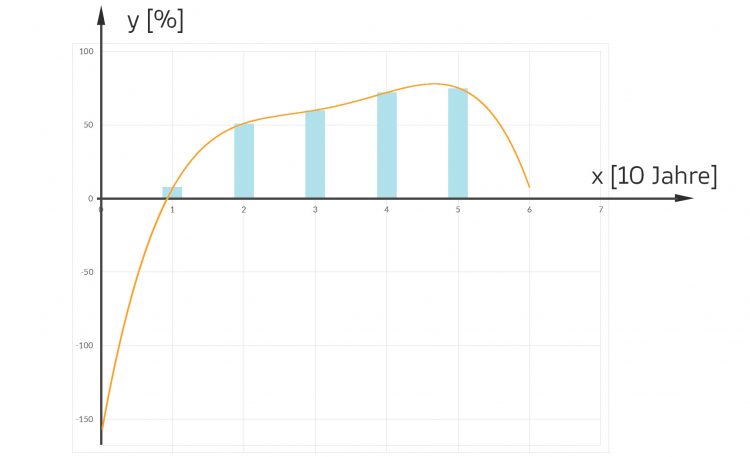
Und das ist die Zeichnung dazu:
Max' Interpretation
Max Hey Rike, das passt ja an Deinen Punkten 
Rike Richtig, schau mal, ich habe ein Polynom 4. Grades erhalten, und der Koeffizient 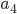
Max Okay! Aber hast Du Deinen eigentlichen Auftrag erfüllt?
Rike Ja, habe ich, ich habe eine Kurve gefunden, die exakt durch alle Punkte 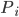
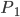
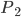
Max Wird das nicht sogar falsch interpretiert werden? Ich stelle mir vor, eine Zeitung schreibt dann: Wissenschaftler haben herausgefunden, dass 60-Jährige genauso wenig wie 10-Jährige die unberührte Natur lieben! Kein 9-Jähriger hat je ein Tier beobachtet!
Rike Aber Max, ich habe doch wirklich nur wenig Information, ich kann doch nicht von den 50-Jährigen auf die 60-Jährigen schließen! Ich brauche weitere Stützstellen am Rand.
Max Vielleicht sollten die Journalisten einen Mathekurs belegen, um das zu verstehen?
Rike Hahaha!
***
Übungsaufgabe
Was ergibt ein Ansatz mit einem Polynom 5. Grades?
Lösung
Man erhält für
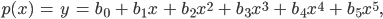
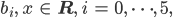
und denselben Funktionswerten ein lineares Gleichungssystem:
Dieses hat 6 Unbekannte und 5 Gleichungen. Erneut mit Gauß oder mit wims.unice.fr/wims/ kann man das schnell lösen und erhält unendlich viele Lösungen mit einem Freiheitsgrad: Die Lösung 4. Grades ist auch dabei.
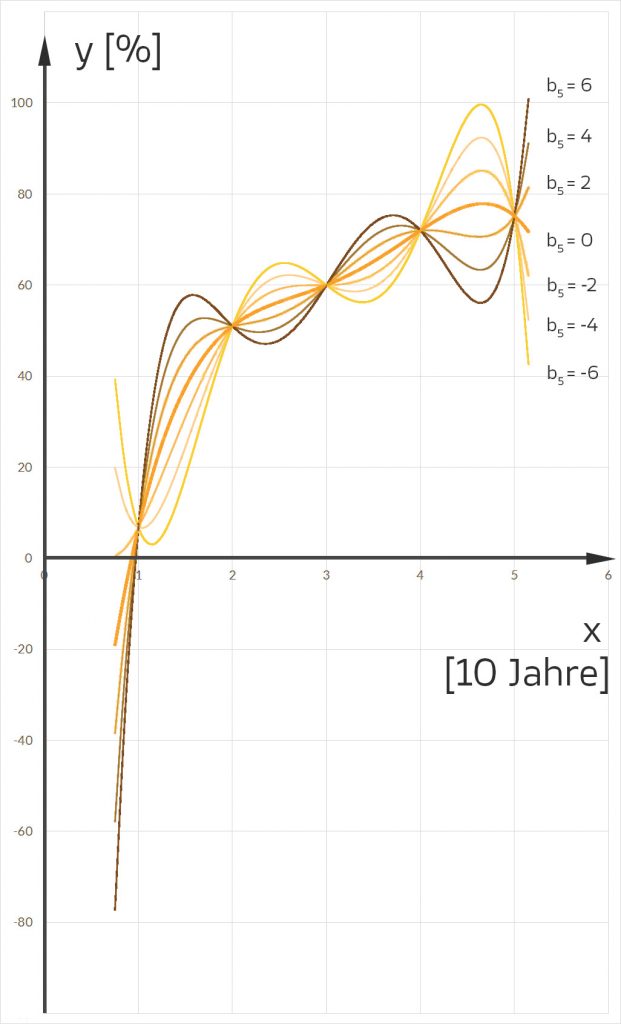
 Es gibt Lösungen mit
Es gibt Lösungen mit  positiv, Null oder negativ.
positiv, Null oder negativ.