Rike hat bereits Überstunden im neuen Job und im ersten Projekt gemacht. Sie hat schon einige Stunden vor ihrem Desktop verbracht. Am Wochenende kommt Max und endlich fährt sie ihren PC runter. Sie gehen in der Senne bei Augustdorf spazieren. Ein wunderbarer Sommertag mit viel Sonne. Am Wegesrand wächst der Hirschwurz-Haarstrang. Sie schauen ihn an und freuen sich über die schönen Formen. An einer einzigen Pflanze kann man verschiedene Stadien der Doldenöffnung sehen. Die Dolden haben Hochblätter, die anfangs die Dolden umschließen, sich dann öffnen und später zurückschlagen. Rike ist fasziniert von der Form und sucht gleich eine Formel dafür.
Rike Max, ich finde organische Formen immer wieder schön.
Max Hmm.
Rike Schau mal, es kann gar nicht so schwer sein, die Form eines Hochblattes zu finden. Was hälst Du denn von 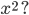
Max Hmm.
Eine Funktion für die Form
Rike Stimmt, eine Normalparabel geht viel zu flach durch den Nullpunkt. Wir nehmen etwas anderes, vielleicht den Tangens – und lassen noch einen freien Parameter 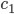
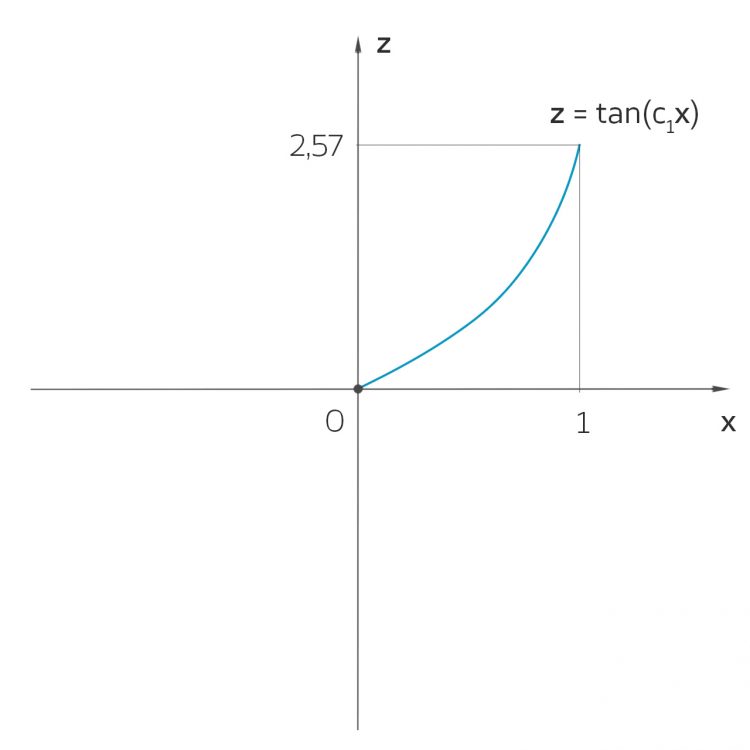
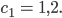
Jetzt müssen wir nur noch dieses Schließen um die Blüte und das Zurückschlagen modellieren.
Max Okay.
Rike Ich glaube, es reicht, die Tangenskurve einfach um den Nullpunkt zu drehen.
Max Wie kann man das ausrechen?
Polarkoordinaten
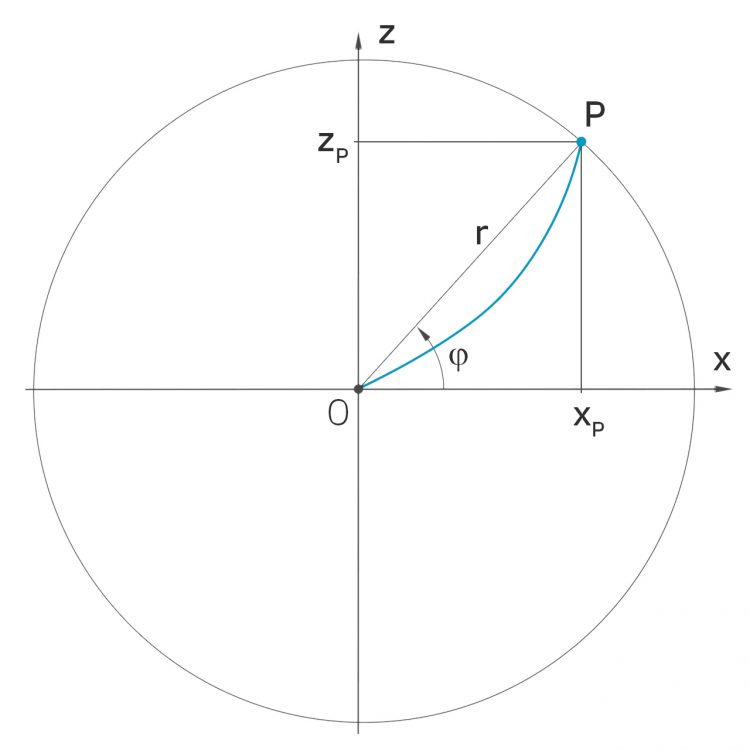
Rike Du bestimmst zu jedem Punkt P auf dem Hochblatt seine Polarkoordinaten:
Du berechnest den Radius r und den Winkel 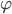
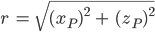
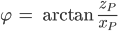
Aus diesen Werten kriegst Du wieder den Punkt
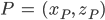
zurück:
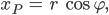
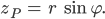
Max Okay.
2D-Drehung für Schließen und Zurückschlagen
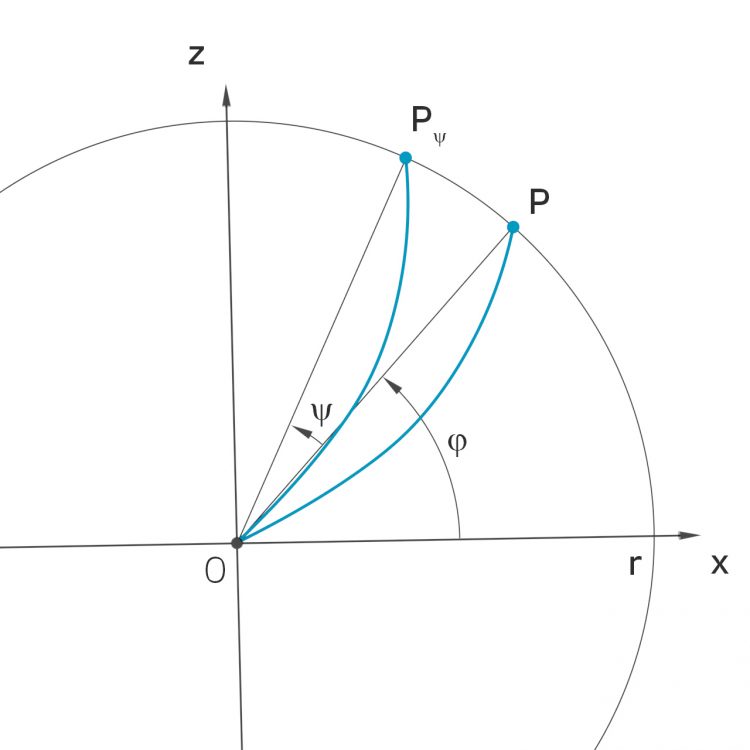
Rike Und wenn Du das hast, dann addierst Du für die Drehung den Drehwinkel 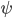
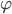
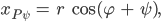
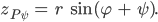
Max Okay.
Rike Das lässt sich prima animieren:
Max Ja, ganz schön. Aber dieser Hirschwurz ist doch 3-dimensional?
Kugelkoordinaten
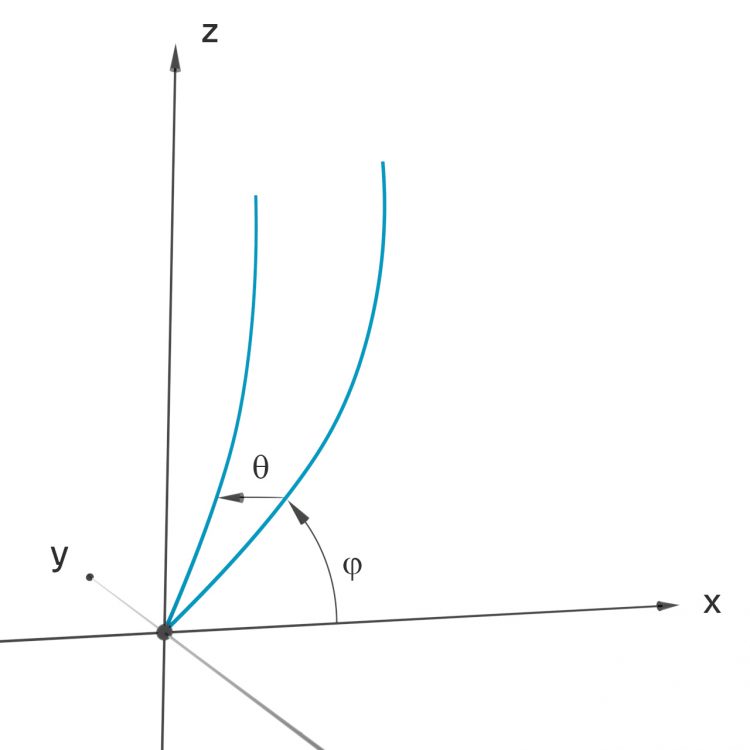
Rike Stimmt. Wenn wir so ein Hochblatt um einen Winkel 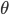
Da haben wir gleich so eine Art Kugelkoordinaten. Du kannst jeden Punkt P mit einem Abstand r zu Null und zwei Winkeln 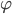
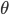
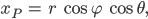
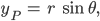
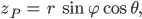
Max Klar, das weiß ich.
Rike Prima, dann haben wir die Hochblätter mit ihren Bewegungen vollständig beschrieben. Was meinst Du, passt das so?
Max Rike, super! Doch ich frage mich, willst Du denn nicht gleich die ganze Senne in mathematischen Formeln schreiben?
Rike Hahaha, ich höre ja auf!
***
Übungsaufgabe
Wie groß ist 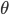
Lösung
45°