Rike gibt heute eine kleine Party in ihrer neuen Wohnung. Sie bereitet mit Max ein paar Cocktails in der Küchenecke vor. Als sie Zitronen und Apfelsinen aufschneiden, fällt Max die Schönheit der Formen auf. Doch Rike meint, dass ist Effizienz, es ist doch ganz normal, jede Fläche in Dreiecke zu zerlegen. Sie erklärt ihm Triangulierung.
Max Hey, Rike guck mal!
Rike Ja, was ist denn?
Max In den Apfelsinen sind schon wieder mathematische Muster versteckt. Wenn man erst mal drauf achtet, findet man sowas ja fast überall, voll cool. Hast du dazu auch ‘ne Formel?
Vertices, Edges und Faces
Rike Hmmmmmm..., äh...., also hier sind schon die Dreiecke bei den zerschnittenen Apfelsinenstückchen, also würde ich sagen, dass Deine Schnittfläche schon mal aus Dreiecken aufgebaut ist. Das hat die Natur gemacht! Da gibt es schöne Beziehungen zwischen der Anzahl der Vertices ...
Max Vertices?
Rike Naja, es gibt Eckpunkte, die Vertices 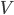
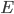
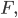
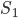 mit Mittelpunkt
mit Mittelpunkt 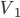
Max Naja, die Vertices, Edges und Faces kann ich zählen, ha, natürliche Zahlen!
Rike Haha!
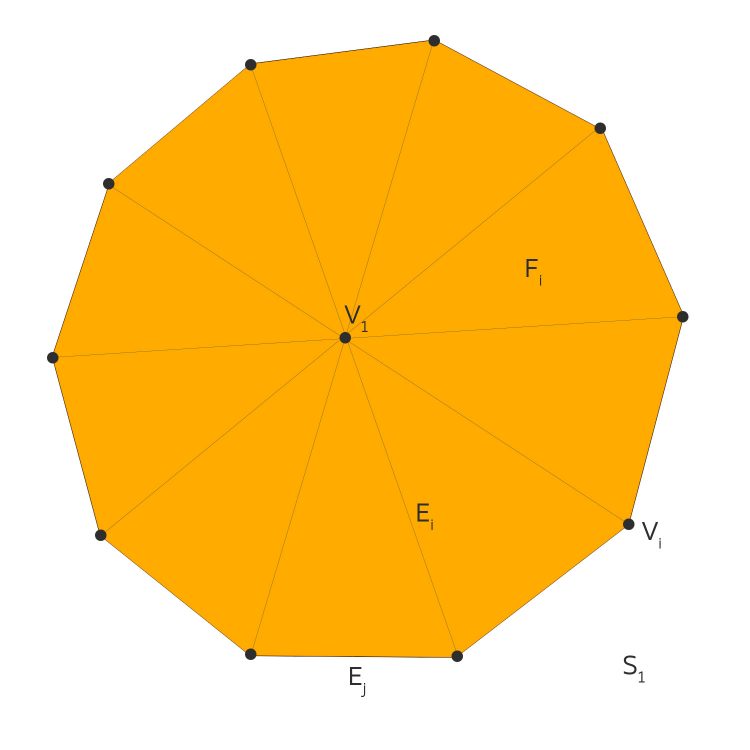
Max Ist ja easy. Die Schnittfläche hat 11 Vertices, 10 Faces und 20 Edges:
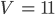
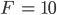
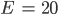
Euler-Charakterstik für S1
Rike Stimmt! Wir können jetzt die sogenannte Euler-Charakterstik 
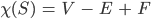
Max Ach, ist ja einfach,
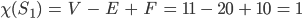
Rike Stimmt! Dreieckszerlegungen werden ziemlich oft benötigt. Bei computergenerierten Images der Apfelsinenhälfte benutzt man die natürlichen Dreiecke, bei der Lösung partieller Differentialgleichungen...
Max Ist okay, Rike.
Natürliche Triangulierung für Apfelsinenhälften
Rike Alles klar! Im Dreidimensionalen ist das nur etwas weniger anschaulich. Aber wir versuchen's mal. An jedes Dreieck der Schnittfläche kommt nun wieder eins, Ai, das hat eine Kante mit der Schnittfläche gemeinsam, und zwischen zwei Ai's kommt jeweils ein Bi, das hat mit der Schnittfläche jeweils einen Vertex gemeinsam.
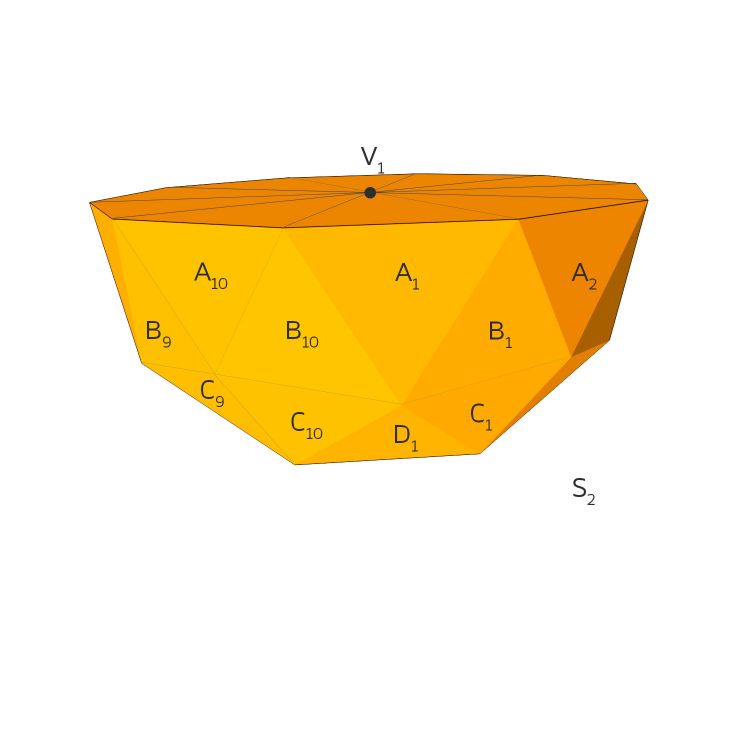
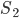
An die Bi's kommen jetzt die Ci's mit jeweils einer gemeinsamen Kante, und an die die Di's mit jeweils 2 gemeinsamen Kanten, aber nur 5 Stück, das siehst Du am besten von unten:
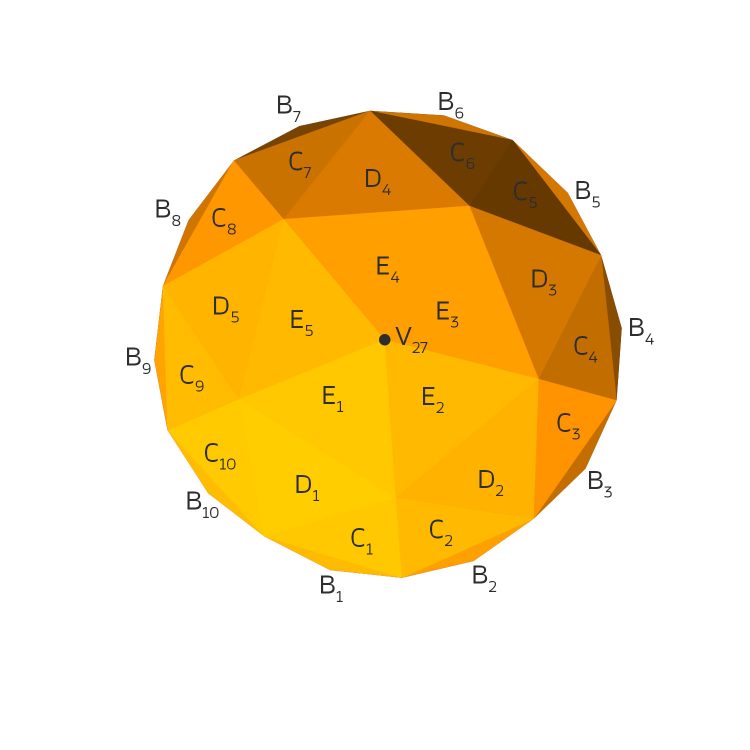
Und zum Schluss die Ei's, die mit den Di's jeweils eine gemeinsame Kante haben.
Max Oh, mein Gott! Kann man die Dreiecke nicht mal alle mit einem Blick sehen? So kann ich gar nicht die Vertices zählen!
Karte der Triangulierung
Rike Na klar! Wir erzeugen so eine Art Projektion – wie bei der Erde. Da kann man eine Karte erzeugen, wo die gesamte Erdkugel drauf ist.
Max Ja, das kenne ich, das gefällt mir, mach mal!
Rike Dazu schneiden wir die Apfelsine am unteren Mittelpunkt entlang der Kanten zwischen den Ei's auf, wart mal, und kriegen dann so eine Karte:
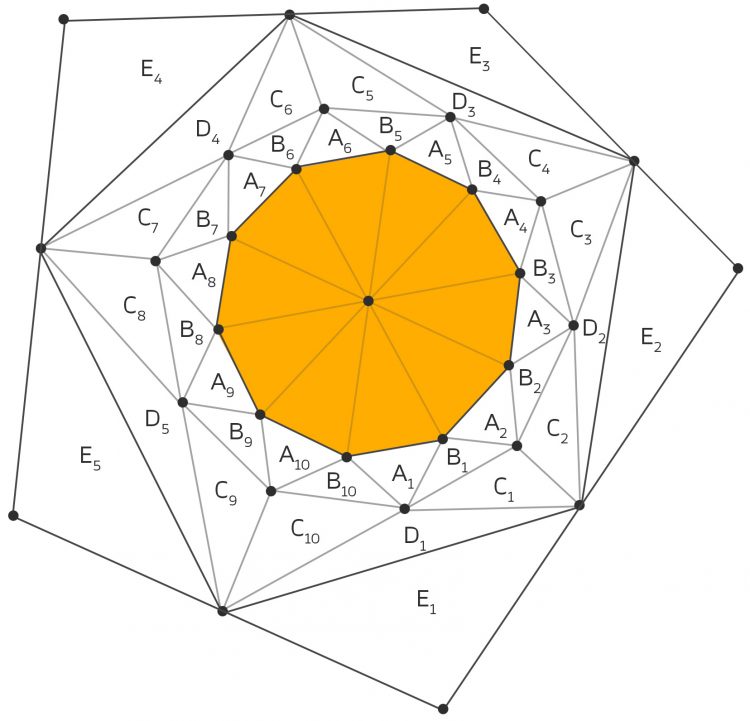
Max Schön, Rike! Für die Vertices kriege ich dann 10 an der Schnittfläche, nochmal 10 bei den Bi's, 5 bei den Di's und außen bei den Ei's haben wir nicht fünf, sondern die zählen nur einmal, weil die 5 im echten, im räumlichen Modell im untersten Vertex zusammenfallen. Und noch den mittleren Vertex 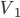
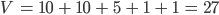
Rike Stimmt!
Max Faces kann man schnell zählen: 10 bei der Schnittfläche, 10 Ai's, 10 Bi's, 10 Ci's, 5 Di's und 5 Ei's:
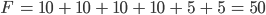
Edges sind etwas mehr, hier darf ich die Äußeren bei den Ei's nicht doppelt zählen.
Formel für die Anzahl der Edges
Rike Da gibt es eine einfache Formel: Im Innern einer Oberfläche hat jede Dreiecksfläche, also jedes Face 3 Edges, doch jedes Edge gehören zu 2 Faces. Du darfst sie nicht doppelt zählen, also
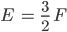
Max Okay, dann haben wir
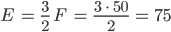
Euler-Charakterstik für S2
Rike Lass uns jetzt mal die Euler-Charakterstik 
Max Na gut:
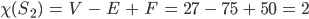
Für die Schnittfläche 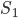
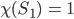
Und jetzt
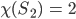
Hm. Was charakterisiert diese Charakteristik eigentlich?
Rike Das ist eine Eigenschaft, die für Flächen bei verschiedenen Triangulierungen invariant bleibt.
Bei 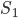
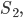
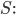
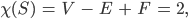
unabhängig von der Triangulierung. Da hast Du eine schöne Formel, um die Korrektheit eines Dreiecksgitters zu prüfen. Ist nämlich
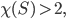
dann gehört die Triangulierung zu einem Objekt mit einem Loch.
Max Ach, Rike, das hättest Du mir früher sagen sollen! Das kenne ich. Komm, wir müssen uns beeilen, gleich kommen die Gäste.
***
Übungsaufgaben
- Überprüfe die Formel für eine andere Triangulierung der Apfelsinenhälfte!
- Gilt die Formel für die Edges auch für S1? Warum?

